Définition de radio de convergence, exemples et exercices résolus

Il Rayon de convergence d'une série de pouvoirs est le rayon du cercle de convergence à laquelle la série converge. Ce cercle s'étend de la valeur qui annule la base des pouvoirs à la singularité la plus proche de la fonction associée à la série.

Toute fonction analytique f (z) Il a associé une série de pouvoirs autour d'un point non-singulaire, appelé Série Taylor:

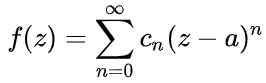
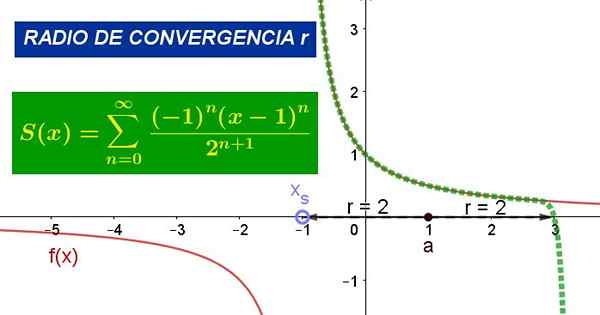
Figure 1. Le graphique montre la série d'alimentation autour de la valeur a = 1 pour la fonction f (x). Son rayon de convergence est r = 2. Source: Fanny Zapata.

Où pour C'est le centre du cercle de convergence, z la variable indépendante de la fonction et le c_n Ce sont des coefficients liés à ceux dérivés de la fonction F Sur le point z = a.

Le rayon de convergence r C'est un nombre réel positif qui définit la région:

| Z - a | < r

Où la série converge. De cette région, la série Diverge, c'est-à-dire qu'elle prend des valeurs infinies. Lorsque le rayon de convergence est infini, la série converge dans tout le plan complexe.

[TOC]

Comment le rayon de convergence est-il déterminé?

Pour qu'une série soit convergente, il est nécessaire que la valeur absolue des termes successives diminuera lorsque le nombre de termes est très important. De manière mathématique, il serait exprimé comme suit:

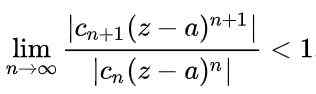
En utilisant les propriétés des limites dans l'expression précédente, elle est obtenue:

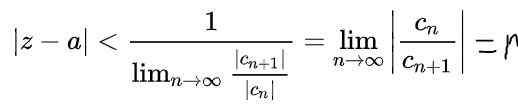
Ici r C'est le rayon de convergence et | Z - a | < r C'est le cercle de bordure ouverte dans le plan complexe où la série converge. En cas de valeur pour et la variable z est un nombre réel, puis l'intervalle ouvert de convergence sur l'axe réel sera: (A - r, a + r).

Série Taylor

La série Taylor d'une fonction f (x) Autour d'une valeur pour Dans lequel la fonction a des dérivés infinis, c'est une série de pouvoirs qui est défini comme:

Il peut vous servir: axiomes de probabilité: types, explication, exemples, exercices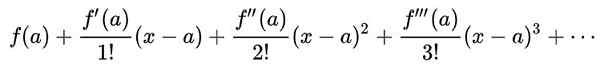

Dans l'environnement | X - A | < r, avec r commeLe rayon de convergence de la série, la série Taylor et la fonction doivent être f (x) Ils coïncident.

D'un autre côté, le rayon de convergence r C'est la distance du point pour Et la singularité X_s plus près du point pour, Être le singulier pointe ces valeurs où la limite de la fonction tend à l'infini.

C'est quand x → x_s ensuite F → ± ∞.

Exemples

Exemple 1

Être S (x) Les pouvoirs donnés par l'expression suivante:

S (x) = 1 - x + x²- X³+ X⁴-.. .+(-1)ⁿ ⋅ xⁿ +.. .

Pour déterminer la région où la série converge, nous calculons le quotient entre le terme (n-beemo + 1) et le terme (n-eme):

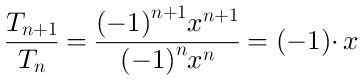
La valeur absolue du quotient antérieur est | x | et sa limite quand N → ∞ c'est aussi  | x |.

Pour que la série soit convergente, il est nécessaire que:

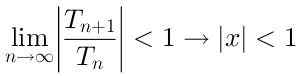
Ainsi, le rayon de convergence de cette série est R = 1, Puisqu'il converge pour les valeurs de x qui sont à une distance inférieure à 1 par rapport au centre x = 0.

Exemple 2

Vous voulez trouver la série Taylor de la fonction f (x) = 1 / (1 + x) autour du point x = 0 et déterminer son rayon de convergence.

Pour trouver la série, nous prenons les dérivés successifs de la fonction f (x), dont nous montrerons les trois premiers:

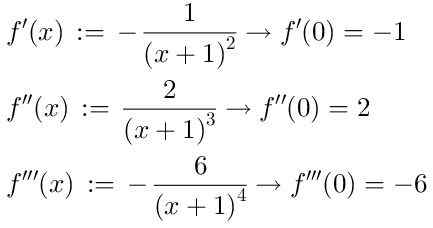
Compte tenu du fait que la durée de commande zéro de la série Taylor est:

 f (0) = 1,

Le premier ordre: F '(0) / 1!

Deuxième ordre:

 F "(0) / 2!

Troisième commande:

 f "(0) / 3!

Et ainsi de suite, la série Taylor de la fonction donnée est:

f (x) = 1 - x + x² - X³ + X⁴ -.. .+(-1)ⁿ ⋅ xⁿ +.. .

Peut vous servir: triangle équilatéral: caractéristiques, propriétés, formules, zone

Qui coïncide avec la série de puissance étudiée dans l'exemple 1.

Nous avons déjà dit que le rayon de convergence d'une série Taylor est la distance du centre de l'expansion en série, qui dans notre cas est la valeur x = 0 Jusqu'à la première singularité de la fonction f (x). 

Comme notre fonction a une singularité (c'est-à-dire une infinité) x = -1, La distance entre la valeur -1 et le centre d'extension 0 est | -1 - 0 | = 1, Il est conclu que le rayon de convergence de la série Taylor est 1.

Ce résultat coïncide pleinement avec celui obtenu dans l'exemple 1 par une autre méthode.

Le fait que la zone de convergence de la série Taylor soit l'intervalle ouvert (-1, 1) implique que la fonction et la série coïncident dans cet intervalle, mais pas en dehors de la même chose.

Qui est illustré à la figure 2, où 41 termes de la série Taylor ont été pris, tracés par la ligne bleue continue, tandis que la fonction d'origine est indiquée sur la ligne rouge des segments.

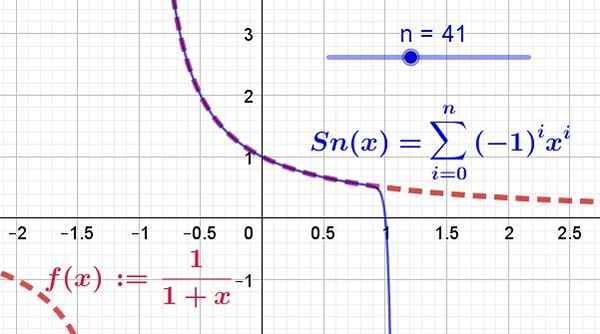Figure 2. La fonction F (x) (en rouge) et sa série de pouvoirs (ou série Taylor en bleu) sont montrées. Il peut être considéré comme les 41 premiers termes de la série convergent entre -1 et 1. De plus, la fonction et sa série coïncident uniquement dans la région de convergence. (Source: Fanny Zapata)

Exercices résolus

- Exercice 1

Considérez la même fonction f (x) = 1 / (1 + x) de l'exemple 2, mais cette fois, il est demandé de trouver la série Taylor de ladite fonction autour du point a = 1.

Solution

Nous trouvons les termes successifs de la série, en commençant par le terme indépendant qui est F (1) = ½.

Le coefficient suivant correspondant au terme de premier ordre est:

F '(1) / 1! = -¼

La deuxième commande est:

f "(1) / 2! = 2 / (2³ 2!)

Suivez le coefficient de troisième commande:

Il peut vous servir: Tetradecágon

f "(1) / 3! = -6 / (2⁴ 3!)

Et ainsi de suite. La série Taylor sera:

Sf (x) = ½ - 1/2² (X-1) + 1/2³(X-1)² - 1/2⁴ (X-1)³ + 1/2⁵ (X-1)⁴-..

- Exercice 2

Trouvez le rayon de convergence de la série précédente

Solution

Nous écrivons le terme n-eme et le terme n-alkaus plus:

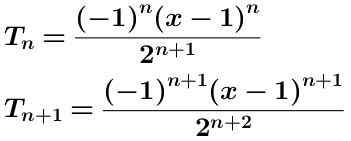Nous calculons le quotient de ces deux termes qui est illustré ci-dessous simplifié:

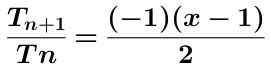
La valeur absolue de l'expression précédente est prise en obtenant:

| X - 1 | / 2

Cependant, pour que la série soit convergente, il est nécessaire que le montant précédent soit strictement inférieur à l'unité, c'est-à-dire:

| X - 1 | < 2

Ce qui indique que le rayon de convergence autour de la valeur x = 1 est:

R = 1

D'un autre côté, l'expression précédente équivaut à double inégalité:

-2 < x - 1 < +2

Si nous ajoutons +1 à chacun des trois membres de l'expression précédente, il est obtenu:

-1 < x < 3

Qui est l'intervalle de convergence de la série.

La figure 1 montre la fonction d'origine et la série Taylor de ladite fonction autour du point x = 1. Dans la figure, il peut être vérifié que la série coïncide avec la fonction dans un environnement de point x = 1, mais dans le rayon de convergence.

Les références

1. Fondation CK-12. Série de puissance: représentation des fonctions et des opérations. Récupéré de: CK12.org.
2. Engler, un. 2019. Calcul intégral. Université nationale de la côte.
3. Larson, R. 2010. Calcul d'une variable. 9na. Édition. McGraw Hill.
4. Textes mathématiques gratuites. Séries de puissance. Récupéré de: mathématiques.Liibretexts.org.
5. Wikipédia. Séries de puissance. Récupéré de: est.Wikipédia.org.
6. Wikipédia. Rayon de convergence. Récupéré de: dans.Wikipédia.org