Quels sont les angles alternatifs internes? (Avec des exercices)

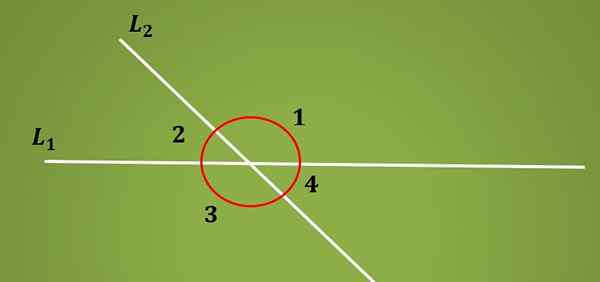
Les angles alternatifs internes Ce sont ces angles formés par l'intersection de deux lignes parallèles et une ligne transversale. Lorsqu'une ligne L1 est coupée par une ligne transversale L2 4 angles sont formés.

Les deux paires d'angles qui restent du même côté de la ligne L1 sont appelées angles supplémentaires, car sa somme est égale à 180º. Dans l'image inférieure, les angles 1 et 2 sont supplémentaires, ainsi que les angles 3 et 4.

Afin de parler d'angles alternatifs internes, il est nécessaire d'avoir deux lignes parallèles et une ligne transversale; Comme vu précédemment, huit angles se formeront.

Lorsqu'il y a deux lignes parallèles L1 et L2 coupées par une ligne transversale, huit angles sont formés, comme illustré dans l'image suivante.

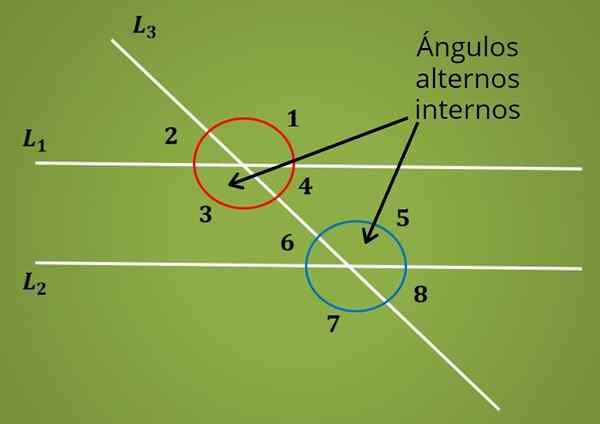
Dans l'image supérieure, les paires d'angles 1 et 2, 3 et 4, 5 et 6, 7 et 8 sont des angles supplémentaires. 

Maintenant, les angles alternatifs internes sont ceux entre les deux lignes parallèles L1 et L2, mais sont situées sur les côtés opposés de la ligne transversale L2. C'est Les angles 3 et 5 sont internes alternatifs. De même, les angles 4 et 6 sont des angles alternatifs internes.

Angles opposés par le sommet

Pour connaître l'utilité des angles alternatifs internes, il est d'abord nécessaire de savoir que si deux angles sont opposés au sommet, alors ces deux angles mesurent le même.

Par exemple, les angles 1 et 3 mesurent les mêmes qu'ils sont opposés par le sommet. Dans le même raisonnement, on peut conclure que les angles 2 et 4, 5 et 7, 6 et 8 mesurent le même.

Angles formés entre un sécant et deux parallèles

Lorsqu'il y a deux lignes parallèles coupées par une ligne sèche ou transversale comme dans la figure précédente, il est vrai que les angles 1 et 5, 2 et 6, 3 et 7, 4 et 8 mesurent le même.

Angles alternatifs internes

En utilisant la définition des angles placés par le sommet et la propriété des angles formés entre une ligne sécante et deux lignes parallèles, on peut conclure que les angles alternatifs internes ont la même mesure.

Exercices résolus

- Premier exercice

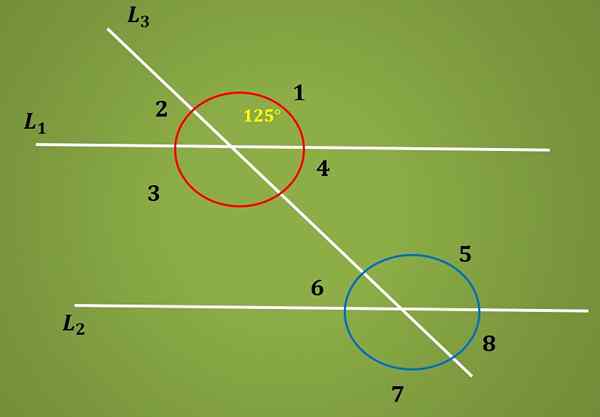
Calculez la mesure de l'angle 6 de l'image suivante, sachant que l'angle 1 mesure 125º.

Solution

Étant donné que les angles 1 et 5 sont opposés par le sommet, vous avez cet angle 3 mesures 125º. Maintenant, comme les angles 3 et 5 sont alternatifs internes, vous avez cet angle 5 mesure également 125º.

Enfin, comme les angles 5 et 6 sont supplémentaires, la mesure de l'angle 6 est nécessaire est égale à 180º - 125º = 55º.

- Deuxième exercice

Calculez l'angle 3 Sachant que l'angle 6 mesure 35º.

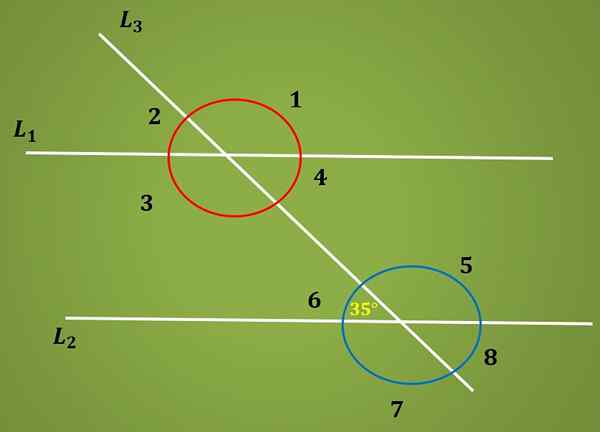
Solution

Il est connu que l'angle 6 mesure 35º, et il est également connu que les angles 6 et 4 sont alternatifs internes, ils mesurent donc le même. C'est-à-dire que l'angle 4 mesure 35º.

En revanche, en utilisant le fait que les angles 4 et 3 sont supplémentaires, la mesure de l'angle 3 est égale à 180º - 35º = 145º.

Observation

Il est nécessaire que les lignes soient parallèles afin qu'ils puissent répondre aux propriétés correspondantes.

Les exercices peuvent être résolus plus rapidement, mais cet article voulait utiliser la propriété des angles alternatifs internes.

Les références

1. Faire boucler. (2007). Un angle sur le manuel de mathématiques de géométrie. Apprentissage de Newpath.
2. Clemens, s. R., O'Dafer, P. g., & Cooney, T. J. (1998). Géométrie. Pearson Education.
3. Lang, S., & Murrow, G. (1988). Géométrie: un cours de lycée. Springer Science & Business Media.
4. Lira, un., Jaime, P., Chavez, m., Gallegos, m., & Rodríguez, C. (2006). Géométrie et trigonométrie. Éditions ombral.
5. Moyano, un. R., Saro, un. R., & Ruiz, R. M. (2007). Algèbre et géométrie quadratique. Netbiblo.
6. Sullivan, m. (1997). Trigonométrie et géométrie analytique. Pearson Education.
7. WINGARD-ENELSON, R. (2012). Géométrie. Enslow Publishers, Inc.