Ce qui représente la longueur du déplacement de l'hexagone

La La longueur du déplacement hexagone représente La longueur des faces latérales du prisme. Pour comprendre cette déclaration, la première chose à savoir est qu'un hexagone est un polygone composé de six côtés.

Cela peut être régulier lorsque tous ses côtés ont la même mesure; ou il peut être irrégulier, quand au moins un côté, il a une mesure différente de celle des autres.

La principale chose qui doit être notée est qu'il y a un hexagone et que cela doit être déplacé, c'est-à-dire, déplacé de lieu, le long d'une ligne qui passe par son centre.

Maintenant, la question est de savoir quelle est la longueur de déplacement précédente? Une observation importante est que les dimensions de l'hexagone n'ont pas d'importance, seule la durée de son mouvement est importante.

Que représente le déplacement?

Avant de répondre à la question du titre, il est utile de savoir ce que représente le déplacement lié à l'hexagone.

Autrement dit, il est basé sur l'hypothèse qu'il y a un hexagone ordinaire, et cela est déplacé d'une certaine longueur, le long d'une ligne qui passe par le centre. Ce qui génère ce déplacement?

S'il est observé en détail, on peut voir qu'un prisme hexagonal est formé. La figure suivante illustre mieux cette question.

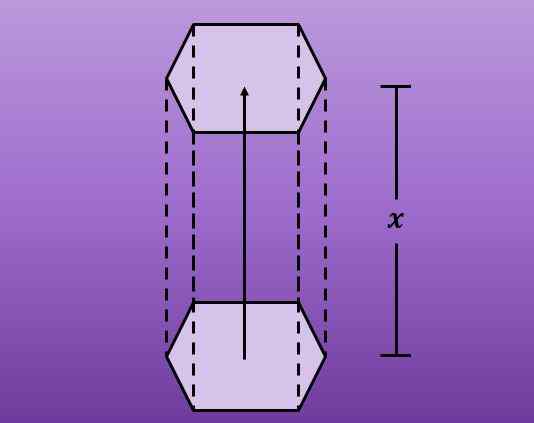
Ce qui représente la longueur du déplacement?

Selon ce qui a été dit, le déplacement génère un prisme hexagonal. Et détaillant l'image précédente, vous pouvez voir que la longueur du déplacement hexagone représente la longueur des visages latéraux du prisme.

La longueur dépend-elle de la direction du déplacement?

La réponse est non. Le déplacement peut être avec n'importe quel angle d'inclinaison et la longueur du déplacement continuera de représenter la longueur des faces latérales du prisme hexagonal formé.

Si le déplacement se fait avec un angle d'inclinaison entre 0 ° et 90 °, un prisme hexagonal oblique sera formé. Mais cela ne change pas l'interprétation.

L'image suivante montre la figure obtenue en déplaçant un hexagone le long d'une ligne inclinée qui passe par son centre.

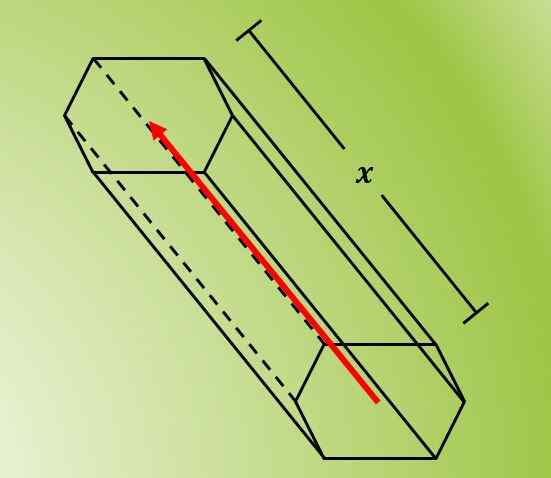
Encore une fois, la longueur du déplacement est la longueur des faces latérales du prisme.

Observation

Lorsque le déplacement est effectué le long d'une ligne perpendiculaire à l'hexagone et qui passe par son centre, la longueur du déplacement coïncide avec la hauteur de l'hexagone.

En d'autres termes, lorsqu'un prisme hexagonal droit se forme, alors la longueur du déplacement est la hauteur du prisme.

Si, au contraire, la ligne a une inclination différente de 90 °, alors la longueur du déplacement devient l'hypoténuse d'un triangle rectangle, où une catégorie dudit triangle coïncide avec la hauteur du prisme.

L'image suivante montre ce qui se passe lorsqu'un hexagone s'affiche en diagonale.

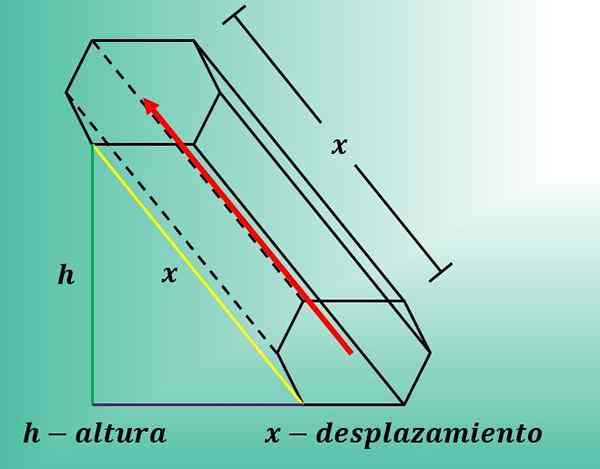
Enfin, il est important de souligner que les dimensions de l'hexagone n'influencent pas la durée du déplacement. 

Ce qui varie, c'est qu'un prisme hexagonal droit ou oblique peut être formé.