Quelle est la relation entre le losange et la zone du rectangle?

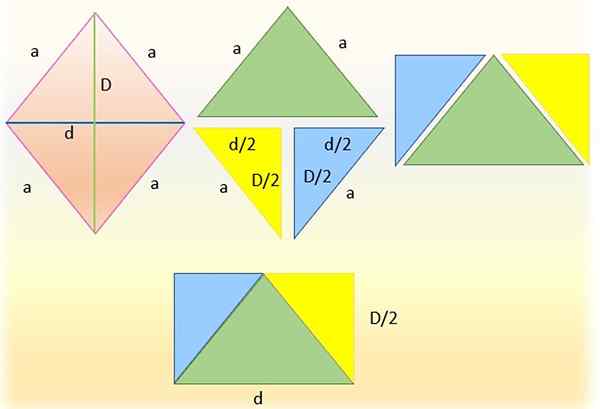
Décomposer un losange pour obtenir un rectangle. Source: F. Zapata

Il est possible de calculer la zone du losange (et quelques autres figures géométriques) à partir de la zone d'un triangle ou d'un quadrilatère apparenté, comme un parallélogramme ou un rectangle.

La zone rectangulaire et parallélogramme est la même: elle est calculée comme le produit entre la base de la figure et sa hauteur par rapport à cette base. Pour sa part, la zone du triangle est le semi-produit entre sa base et sa hauteur.

Ces formules sont faciles à retenir, bien que, naturellement, la géométrie offre une formule exclusive pour la zone de losange, connaissant la mesure de ses diagonales majeures et mineures, désignées respectivement d et d, respectivement:

Il est possible de déduire cette expression à travers la séquence illustrée dans la figure ci-dessus.

Pour ce faire, le losange de gauche est coupé par l'une de ses diagonales, qui a été faite dans la section figure par la diagonale mineure, obtenant ainsi deux triangles. Le triangle supérieur (en vert) est laissé et celui inférieur est divisé à son tour en deux triangles, coupant dans la moitié de la diagonale majeure, obtenant les triangles rectangles bleu et jaune identiques.

Ensuite, les hypotenus de ces triangles coïncidaient avec les côtés du triangle vert, car ils mesurent la même chose, c'est-à-dire «A». Et un rectangle est enfin obtenu, dont la base est la diagonale «D» inférieure et dont la hauteur est la moitié de la diagonale majeure, c'est-à-dire: «D / 2».

La zone du rectangle ainsi formé coïncide exactement celle du losange, il peut donc être confirmé que:

Peut vous servir: trinomial

POUR _diamant = (base × hauteur) _rectangle = D × (d / 2)

Un résultat qui, comme on peut le voir, coïncide exactement avec la formule de la zone de lossification donnée avant.

Rombo et zone de parallélogramme

La zone du losange est également liée à celle d'un parallélogramme, car les deux figures géométriques sont plates et appartiennent à la famille des quadrilatères. Par exemple, dans l'image suivante, il y a un losange à gauche et un parallélogramme à droite.

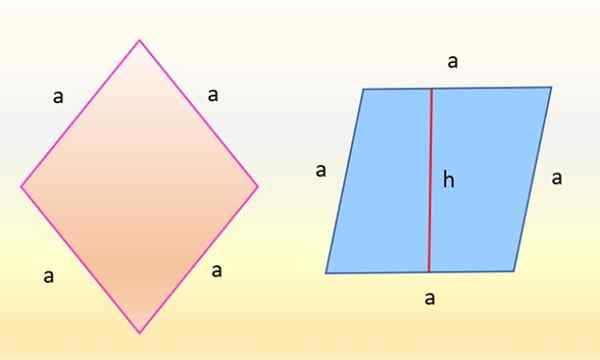La zone de rhombus à gauche est la même que celle du parallélogramme à droite. Source: F. Zapata

Il s'avère que les chiffres sont identiques, car ce qui a changé n'est que l'orientation. Le losange à gauche, en rose, dont les côtés ont la même mesure: a, il est tourné de telle manière que l'un de ses côtés est complètement horizontal. Ensuite, le rhombus prend la forme du parallélogramme bleu à droite.

Et l'aire de ce parallélogramme est également le produit entre la base "A" et la hauteur par rapport à cette base, appelée "h" sur la figure, donc:

POUR _{parallélogramme} = A × h

Comme c'est la même figure, la zone est identique et suit que:

POUR _diamant = A × h

Ainsi, sachant et h du parallélogramme, sa zone est calculée et elle coïncidera avec celle du losange.

Zone coucho inscrite dans un rectangle

Une autre relation entre le losange et le rectangle apparaît lorsque le premier est enregistré à l'intérieur du second. Si cela se produit, les sommets du rhombus coïncident avec le point médian des côtés du rectangle, qui est affiché ci-dessous:

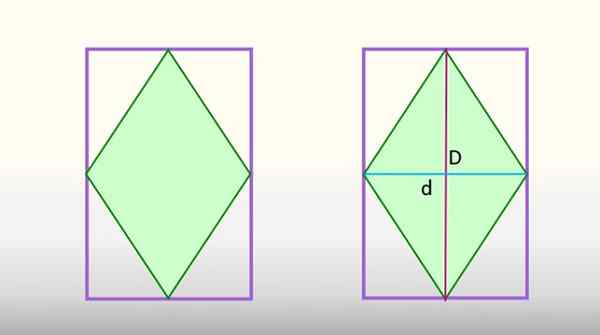La zone du losange inscrit dans le rectangle équivaut à la moitié de la zone rectangulaire. Source: F. Zapata

Cette disposition rend les diagonales majeures et mineures du losange, la figure est divisée en 8 triangles identiques, dont 4 correspondent au losange, en vert, et les 4 autres font partie du rectangle. Si ces 4 derniers triangles se joignaient, ils formeraient la moitié du rectangle et les 4 triangles de rhombus, l'autre.

Il peut vous servir: triangle isocèle

Par conséquent, la zone du losange équivaut à la moitié de la zone rectangulaire dans laquelle il est enregistré, déclarant que:

POUR_diamant = A_rectangle / 2

Ceci est facilement vérifié en calculant l'aire de l'un des triangles et en multipliant par 4, car ils sont identiques. La zone de tout triangle est la moitié du produit entre la base et sa hauteur:

POUR _Triangle = base × hauteur / 2

À partir de la figure précédente, il est observé que la base de l'un des triangles est d / 2 et que la hauteur est d / 2, que le remplacement dans la formule précédente donne:

POUR _Triangle = (d / 2) × (d / 2) / 2 = (d × d) / 8

Multipliez ce résultat par 4 pour avoir la zone de lossification:

POUR _diamant = 4 (d × d) / 8 = (d × d) / 2

Pour sa part, la moitié du rectangle est:

POUR _rectangle / 2 = base × hauteur / 2

Comme la base du rectangle est d et sa hauteur est d, elle reste:

POUR_rectangle / 2 = d × d / 2

Qui est précisément la zone du losange enregistré. Il est alors conclu que:

La zone d'un losange enregistré dans un rectangle équivaut à la moitié de la zone de cette.

Exercices résolus

Exercice 1

Quelle est la quantité de lossiliers dont la principale diagonale mesure 14 mesures 14.6 cm et la diagonale inférieure 9.8 cm?

Solution

En remplaçant d = 14.6 cm et d = 9.8 cm dans la formule de la zone du losange:

La zone recherchée est:

POUR _diamant = 14.6 cm × 9.8 cm = 143.1 cm²

Exercice 2

Sur la figure de la section précédente, la principale diagonale du losange enregistré dans le rectangle mesure d = 30 cm et la zone rectangulaire vaut 210 cm². Il est demandé de calculer:

a) La longueur de la diagonale mineure

Il peut vous servir: segment de ligne et semi-rovi

b) la zone du losange, de deux manières: la première à travers la zone rectangulaire et la seconde en utilisant la formule de la zone d'un losange. Vérifiez que le résultat est le même.

Solution à

La zone rectangulaire est le produit entre sa base et sa hauteur. La plus grande diagonale est sa hauteur, tandis que la plus petite diagonale d serait la base. En utilisant la formule de zone et en remplaçant les valeurs de l'instruction, vous avez:

POUR _rectangle = base × hauteur = d × 30 cm = 210 cm²

Ensuite, la base vaut:

D = 210 cm² / 30 cm = 7 cm

Solution B

Comme on le voit ci-dessus, la zone du losange est la moitié de la zone du rectangle, et cela est connu:

POUR _diamant = 210 cm² / 2 = 105 cm²

Le résultat est vérifié immédiatement, en remplaçant dans la formule:

Les diagonales sont déjà connues: d = 30 cm, d = 7 cm, alors:

POUR _diamant = 30 cm × 7 cm / 2 = 105 cm²

Il est prouvé que, comme prévu, la zone de lossification est la même dans les deux cas.