Quel est le moment magnétique?

Il Moment magnétique C'est un vecteur qui relie le courant qui traverse un peu ou une boucle fermée avec la zone de la même. Son module est égal au produit de l'intensité du courant par la zone, et sa direction et sa direction sont données par la règle de droite, comme le montre la figure 1.

Cette définition est valable malgré tout. Quant à l'unité du moment magnétique, dans le système international d'unités s'il est ampère × m².

Figure 1. Le vecteur de moment magnétique d'une obligation de courant arbitraire est perpendiculaire à son plan et la direction est déterminée par la règle du pouce droit. Source: Wikimedia Commons.

En termes mathématiques, indiquant le moment magnétique vectoriel avec les paroles grecques μ (En gras parce qu'il s'agit d'un vecteur et se distingue donc de son ampleur), il est exprimé comme:

μ = Ia n

Où je suis l'intensité du courant, a est la zone qui entoure la boucle et n C'est le vecteur unitaire (du module égal à 1) qui pointe dans la direction perpendiculaire au plan de la spase, et dont la signification est donnée par la règle du pouce droit (voir figure 1).

Cette règle est très simple: recroqueviller les quatre doigts de la main droite afin qu'ils suivent le courant, le pouce indique la direction et la direction de n Et donc le moment magnétique.

L'équation précédente est valable pour une boucle. S'il y a des nougas comme dans une bobine, le moment magnétique est multiplié par n:

μ = nIa n

[TOC]

Moment magnétique et champ magnétique

Il est facile de trouver des expressions pour le moment magnétique de virages avec des formes géométriques régulières:

-Côté carré du côté ℓ: μ = Je² n

-Côtés spirale rectangulaire pour et b: μ = IAB n

-Radio R. Radio Spira: μ = Iπr² n

Peut vous servir: numéro atomique

Champ magnétique de Dipolo

Le champ magnétique produit par la boucle actuelle ou la spase ressemble à celui d'un aimant de barre et aussi de celui de la Terre.

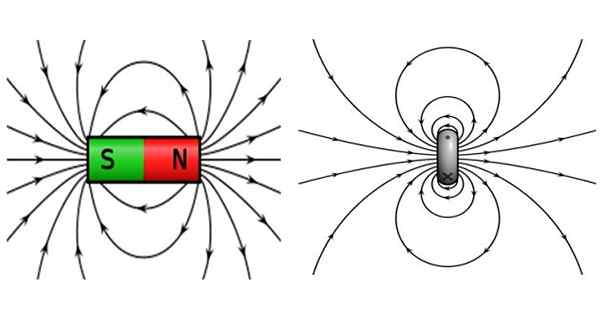Figure 2. À gauche, le champ magnétique d'un aimant de barre et à droite qui produit une spirale circulaire qui transporte le courant. Source: Wikimedia Commons.

Les aimants de barres sont caractérisés par le pôle Nord et le pôle Sud, où les pôles opposés sont attirés et les mêmes pôles repoussent. Les lignes de champ sont fermées, quittent le pôle Nord et atteignent le pôle Sud.

Maintenant, les pôles magnétiques sont inséparables, ce qui signifie que si un aimant de barre est divisé en deux aimants plus petits, ils continuent d'avoir leurs propres pôles nord et sud. Il n'est pas possible d'avoir les pôles magnétiques isolés, c'est pourquoi l'aimant de barre est appelé Dipolo magnétique.

Le champ magnétique d'un rayon R Spiral R, qui transporte un courant I, est calculé par la loi biot-éventée. Pour les points appartenant à son axe de symétrie (dans ce cas l'axe x), le champ est donné par:

Où μ_soit C'est la perméabilité du vide. Prenant le terrain à des points loin de la spase, pour laquelle il est accompli que x >> r, le terrain s'approche:

Relation entre le champ magnétique et le moment magnétique du dipolo

Y compris le moment magnétique dans l'expression précédente est:

De cette façon, l'intensité du champ magnétique est proportionnelle au moment magnétique. Notez que l'intensité du champ diminue avec le cube de distance.

Cette approche est applicable à toute boucle, tant que X être grand par rapport à ses dimensions.

Et comme les lignes de ce champ ressemblent à celles de l'aimant de barre, l'équation est un bon modèle pour ce champ magnétique et celui d'autres systèmes dont les lignes sont similaires, comme: par exemple:

Peut vous servir: absorbance: quels sont les exemples et les exercices résolus

-Particules chargées en mouvement comme électronique.

-L'atome.

-Terre et autres planètes et satellites du système solaire.

-Étoiles.

Effet d'un champ externe sur la boucle

Une caractéristique très importante du moment magnétique est son lien avec le couple que la boucle expérimente en présence d'un champ magnétique externe.

Un moteur électrique contient des bobines à travers lesquelles un flux de direction changent et que grâce au champ externe expérimente un effet de virage. Ce virage fait bouger un axe et l'énergie électrique devient une énergie mécanique pendant le processus.

Couple sur une boucle rectangulaire

Supposons, pour faciliter les calculs, un côté rectangulaire pour et b, dont le vecteur normal n, Écran sortant, initialement il est perpendiculaire à un champ magnétique uniforme B, Comme dans la figure 3. Les côtés de la boucle d'expérience forces données par:

F = IL X B

Où L C'est un vecteur de magnitude égal à la longueur du segment et dirigé en fonction du courant, et c'est l'intensité de la même et B C'est le champ. La force est perpendiculaire aux deux L Comme le champ, mais tous les côtés ne ressentent pas la force.

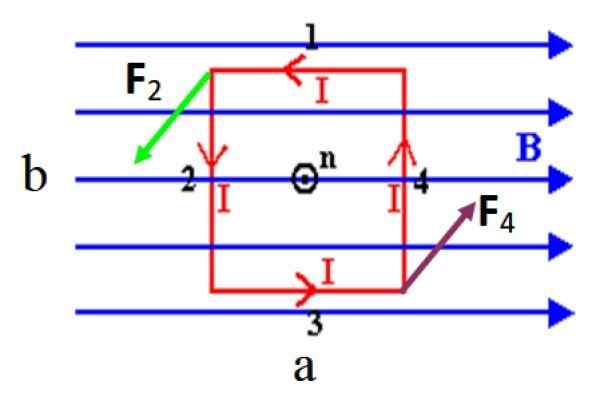figure 3. Une spirale rectangulaire qui transporte un actuel I dans un sens anti-horaire, éprouve un couple en présence d'un champ magnétique uniforme uniforme. Source: F. Zapata.

Dans la figure illustrée, il n'y a aucune force sur les côtés courts 1 et 3 pour être parallèle au champ, n'oubliez pas que le produit transversal entre les vecteurs parallèles est vide. Cependant, les côtés longs 2 et 4, qui sont perpendiculaires à B, Ils éprouvent des forces dénotées comme F₂ et F₄.

Ces forces se forment une paire: Ils ont la même ampleur et la même direction, mais les sens opposés, ils ne sont donc pas en mesure de se déplacer vers la boucle au milieu du champ. Mais ils peuvent le faire tourner, car le couple  τ Que chaque force exerce, par rapport à l'axe vertical qui passe par le centre de la boucle, il a la même direction et la même signification.

Peut vous servir: force de cohésion

Selon la définition du couple, où r C'est le vecteur de position:

τ = r X F

Ensuite:

τ₂ = τ₄=(A / 2) f (+J )

Les couples individuels ne sont pas annulés, car ils ont la même direction et le même sens, alors ils sont ajoutés:

τ_filet = τ₂ + τ₄ = a f (+J )

Et étant l'ampleur de la force F = IBB, il en résulte:

τ_filet = I⋅a⋅b⋅b (+J )

Le produit A⋅B est la zone A de la spase, donc IAB est l'ampleur du moment magnétique μ. Donc τ_filet = μ⋅B (+J )

On peut voir que, en général, le couple coïncide avec le produit vectoriel entre les vecteurs μ et B:

τ_filet = μ X B

Et bien que cette expression soit dérivée d'une boucle rectangulaire, elle est valable pour une implanture plate arbitraire.

L'effet du champ sur la boucle est un couple qui a tendance à aligner le moment magnétique avec le champ.

Énergie potentielle du dipôle magnétique

Pour tourner la spirale ou le dipôle au milieu du champ, une œuvre doit être effectuée contre la force magnétique, ce qui modifie l'énergie potentielle du dipolo. La variation de l'énergie ΔU, lorsque la spirale tourne de l'angle θ_soit À l'angle θ est donné par l'intégrale:

Si le niveau de référence est choisi comme θ_soit = π / 2:

ΔU = -μB cos θ

Qui à son tour peut être exprimé comme le produit scalaire entre les vecteurs B et μ:

Δu = - μ ·B

L'énergie potentielle minimale dans le dipôle se produit lorsque Cos θ = 1, ce qui signifie que μ et B Ils sont parallèles, l'énergie est maximale s'ils sont opposés (θ = π) et sont nuls lorsqu'ils sont perpendiculaires (θ = π / 2).

Les références

1. Figueroa, D. 2005. Série: Physique pour la science et l'ingénierie. Volume 5. Électromagnétisme. Édité par Douglas Figueroa (USB).
2. Resnick, r. 1999. Physique. Vol. 2. 3e édition. en espagnol. Société de rédaction continentale S.POUR. de c.V.
3. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. 2ieme volume. Pearson.
4. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. 2ieme volume. 7e. Élégant. Cengage Learning.
5. Tipler, P. (2006) Physique de science et de technologie. 5e ed. 2ieme volume. Éditorial Revered.