Page d'accueil
Matematiques
Limiter les propriétés (avec des exemples)

Matematiques

Limiter les propriétés (avec des exemples)

1202
315
Paul Dumas

Le Limiter les propriétés Ils sont l'ensemble des règles et procédures algébriques utilisées pour les déterminer. Le concept limite est essentiel pour le calcul et trouver sa valeur ne doit pas être une tâche compliquée, à condition que ses propriétés soient gérées avec facilité.

Vous trouverez ci-dessous une liste des plus importantes, accompagnées d'exemples d'application.

Les limites et ses propriétés sont à la base du calcul. Une limite très spéciale est indiquée sur la figure: la dérivée d'une fonction f (x)

Laissez les nombres réels b, c, n, a et b, et F et g de telles fonctions qui vérifient ce qui suit:

$\lim_x\rightarrow cf(x)=A$
$\lim_x\rightarrow cg(x)=B$

Ensuite, vous avez les propriétés suivantes:

1. Limite de remplacement direct

Dans le premier cas, la limite d'une fonction F lorsque X → C peut être calculée en remplacement directement x = C dans la fonction. Si la fonction existe à x = c, alors la limite est:

$\lim_x \rightarrow c f(x)=f(c)$ Mais pas nécessairement la fonction doit être définie à x = c pour que la limite existe. L'idée est d'approcher autant que vous voulez la valeur de x = c et de voir ce qui se passe avec la fonction dans ce cas.

Exemple

Trouvez la limite de f (x) = x² Quand x → 4

Solution

La limite résout simplement en remplaçant x = 4 en f (x) = x², Puisqu'il n'y a aucun inconvénient à effectuer l'opération:

$\lim_x\rightarrow 4x^2=4^2=16$ 2. L'unicité de la limite

Si la limite d'une fonction f (x) lorsque X → C existe et vaut L, ladite limite est unique.

Par conséquent, les limites latérales, qui sont celles où x → c^- (Lire «X tend à C de la gauche») et quand X → C⁺(Il se lit.

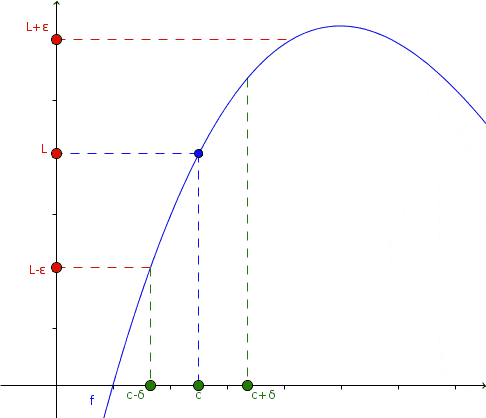Dans cette animation, le concept de limite est présenté: Lorsque X tend à une certaine valeur C, s'approchant à la fois à gauche et à droite, la valeur de la fonction tend à L. Pas nécessairement la fonction est définie dans x = c. Source: Wikimedia Commons.

Dans l'animation, cette approche est observée et ce qui se passe avec la fonction dans ce cas: s'il s'approche à gauche et à droite à x = c, la valeur de la fonction à son tour est proche de L.

Peut vous servir: carrés minimaux

Exprime mathématiquement de cette façon:

$\lim_x\rightarrow c^-f(x)=\lim_x\rightarrow c^+f(x)=\lim_x\rightarrow cf(x)=L$ Les limites latérales permettent de savoir quand une limite existe ou non, car si elles n'existent pas ou si elles diffèrent, il est certain que la limite de la fonction lorsque x → C n'existe pas.

Exemple

Calculez la limite de f (x) lorsque x → 1 s'il existe, où f (x) est donné par:

Solution

Ceci est une fonction de parties ou définie en pièces, qui se compose de la ligne 4 -x pour les valeurs de x < 1 y en la parábola 4 - x² Lorsque x est égal à 1 ou supérieur à 1.

Nous pouvons aborder x = 1 de la gauche, dans ce cas, la partie de la fonction qui est valable pour x est prise<1:

Comme les limites latérales sont les mêmes, il s'ensuit que la limite de la fonction lorsque x → 1 existe et vaut 3.

3. Constant

La limite d'une constante est la valeur de ladite constante, quelle que soit la valeur à laquelle la variable tend:

$\lim_x\rightarrow cb=b .$

Exemple

Calculer:

$\lim_x\rightarrow 1\pi$ Solution

$\lim_x\rightarrow 1\pi= \pi$

4. Limite de fonction d'identité

Si f (x) = x, il est toujours accompli que:

$\lim_x\rightarrow cx=c$

Exemple

Calculer:

$\lim_x\rightarrow 2x$ Solution

$\lim_x\rightarrow 2x=2$

5. Limite de produit d'une constante par une fonction

Dans ce cas, la constante sort de la limite et se déplace pour le multiplier, comme ceci:

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Exemple

Calculez, s'il existe, la limite suivante:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Solution

La constante 5 est à l'extérieur se multiplier à la limite et la propriété de remplacement est appliquée:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]=5\cdot \lim_x\rightarrow -2 x^3=5\cdot (-2)^3=-40$

6. Limite de somme

La limite de la somme de deux fonctions F et g C'est la somme des limites:

$\lim_x\rightarrow c\left [ f(x)+g(x) \right ]=\lim_x\rightarrow c f(x)+\lim_x\rightarrow cg(x)=A+B$

Exemple

Trouvez la limite suivante si elle existe:

Peut vous servir: Théorie des ensembles: caractéristiques, éléments, exemples, exercices

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Solution

La propriété de la somme des limites est appliquée d'abord puis celle du remplacement direct, car les opérations ne présentent pas de difficulté:

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ] = \lim_\theta \rightarrow \pi cos\: \: \theta + \lim_\theta \rightarrow \pisen\: \: \theta=cos\: \pi +sen\: \pi =-1$

7. Limite de soustraction

Dans le cas de la limite de la soustraction de deux fonctions, procurez-vous de manière analogue que pour la somme: la limite de la soustraction est la soustraction des limites:

$\lim_x\rightarrow c \left [f(x) - g(x) \right ]=A-B$

Exemple

Calculez la limite suivante:

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Solution

La propriété de la limite de soustraction de deux fonctions est appliquée puis le remplacement direct, car toutes les opérations peuvent être effectuées sans problème:

$\lim_x \rightarrow 0 [sec\: x - e^x ]=\lim_x \rightarrow 0 sec\: x -\lim_x \rightarrow 0 e^x = sec\: 0-e^0=1-1=0$

8. Limite de produit

La limite de produit de deux fonctions F et g C'est le produit des limites:

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Exemple

Calculez cette limite:

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)$

Solution

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)=\lim_x \rightarrow 0 cos\: x\cdot \lim_x \rightarrow 0 (1-x^2^)=cos\: 0\cdot (1-0^2)=1$

9. Rapport du quotient

La limite du rapport de deux fonctions F et g C'est le quotient des limites, à condition que la limite de g (x) lorsque x → c soit différente de 0, car la division de 0 n'est pas définie. Ensuite:

$\lim_x \rightarrow c \left [ \fracf(x)g(x) \right ]=\frac\lim_x \rightarrow c f(x)\lim_x \rightarrow c g(x)=\fracAB; \: \: \textupcon\: B\neq 0$

Exemple

Calculez, s'il existe, la valeur de la limite suivante:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Solution

Dans le premier cas, la propriété de la propriété est appliquée, pour obtenir le quotient des limites:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]=\frac\lim_x \rightarrow -3 2x-6\lim_x \rightarrow -3 x^2+5$

La propriété de remplacement est maintenant appliquée pour trouver chaque limite:

$\lim_x \rightarrow -3 2x-6=2\cdot (-3)-6=-12$ $\lim_x \rightarrow -3 x^2+5= (-3)^2+5=14$

Et depuis b ≠ 0, la limite recherchée est le quotient a / b:

$\lim_x \rightarrow -3 \frac2x-6x^2+5=\frac-1214=\frac-67$

dix. Limite

La limite d'une puissance de l'exposant n est équivalente à la limite soulevée à ladite puissance, comme suit:

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Cas 1: Limite d'une puissance X

Si vous avez, par exemple, la limite d'une puissance X, résultats:

$\lim_x \rightarrow c x^n=\left [\lim_x \rightarrow c x \right ]^n$

Selon la propriété 4, cette limite est:

Peut vous servir: analogies numériques: types, applications et exercices

$\lim_x \rightarrow c x^n=c^n$

Cas 2: limite de racine

Une racine n-cette racine peut être écrite sous la forme d'un exposant fractionnaire, donc:

$\lim_x \rightarrow c \sqrt[n]f(x)=\sqrt[n]\lim_x \rightarrow c f(x)$

Important: Si l'indice de racine est égal, il est nécessaire que la limite de f (x) lorsque x → c soit supérieure ou égale à 0, car il n'y a pas de vraies paires de quantités négatives.

Exemples

Déterminer, en appliquant les propriétés précédentes, les limites suivantes s'ils existent:

$a)\: \lim_x \rightarrow -2 (x+5)^^3$

$b)\: \lim_x \rightarrow 3 \sqrt2x-1$

Solution à

Par la propriété de la limite d'une puissance et de la substitution directe, il est obtenu:

$\lim_x \rightarrow -2 (x+5)^^3= \left [\lim_x \rightarrow -2 (x+5) \right ]^3=(-2+5)^3=27$

Solution B

$\lim_x \rightarrow 3 \sqrt2x-1=\sqrt\lim_x \rightarrow 3 \left (2x-1 \right )=\sqrt(2\cdot 3-1)=\sqrt5$

onze. Limite

Pour trouver la limite d'une base exponentielle B et exposant f (x), la base de la fonction de la fonction f (x) doit être soulevée comme suit:

$\lim_x \rightarrow c \left [b^f(x) \right ]=b^\lim_x \rightarrow cf(x)$

Exemple

Trouvez s'il y a la limite suivante:

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Solution

Dans cette limite, la base est le nombre e et la fonction f (x) = x², Par conséquent, vous devez d'abord calculer la limite X² Lorsque x tend à 1:

$\lim_x \rightarrow 1 x^2=1^^2=1$

Alors la propriété de la limite exponentielle est appliquée:

$\lim_x \rightarrow 1 e^^x^2=e^^1=e$

12. Limite de fonction potentielle exponentielle

La limite lorsque x → c d'une fonction f (x), qui à son tour est élevée à une autre fonction g (x) est exprimée par:

$\lim_x \rightarrow c \left [f(x)^g(x) \right ]=\left [\lim_x \rightarrow c f(x) \right ]^\lim_x \rightarrow c g(x)$

Exemple

Calculez la limite suivante, si elle existe:

$\lim_x \rightarrow -1 (x-1)^^2x$

Solution

Pour appliquer la propriété précédente, ils sont d'abord identifiés f (x) = x-1 et g (x) = 2x, puis les limites respectives sont calculées:

$\lim_x \rightarrow -1 (x-1)=-1-1=-2$

$\lim_x \rightarrow -1 2x=2\cdot (-1)=-2$ Finalement:

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Les références

Ayres, f. 2000. Calcul. 5ed. Mc Graw Hill.
Leithold, L. 1992. Calcul avec géométrie analytique. Harla, s.POUR.
Textes mathématiques gratuites. Limites. Récupéré de: mathématiques.Liibretexts.org.
Mathémovil. Lois et limiter les propriétés. Récupéré de: Matemovil.com.
Larson, R. 2010. Calcul d'une variable. 9na. Édition. McGraw Hill.
Purcell, E. J., Varberg, D., & Rigdon, s. ET. (2007). Calcul. Mexique: Pearson Education.
Formules d'univers. Limiter les propriétés. Récupéré de: universoformules.com

Limiter les propriétés (avec des exemples)

1. Limite de remplacement direct

Exemple

Solution

2. L'unicité de la limite

Exemple

Solution

3. Constant

Exemple

Solution

4. Limite de fonction d'identité

Exemple

Solution

5. Limite de produit d'une constante par une fonction

Exemple

Solution

6. Limite de somme

Exemple

Solution

7. Limite de soustraction

Exemple

Solution

8. Limite de produit

Exemple

Solution

9. Rapport du quotient

Exemple

Solution

dix. Limite

Cas 1: Limite d'une puissance X

Cas 2: limite de racine

Exemples

Solution à

Solution B

onze. Limite

Exemple

Solution

12. Limite de fonction potentielle exponentielle

Exemple

Solution

Les références

Meilleurs articles

Symptômes, causes et traitements de la pyromanie

La pyromanie est une altération psychique définie comme un trouble de contrôle des impulsions. Il s'...

Biographie de Lola van Wagenen

Lola Van Wagenen (décembre 1938) est un historien américain qui était co-polonais de Consumer Action...

$\lim_x\rightarrow 4x^2=4^2=16$ 2. L'unicité de la limite

$\lim_x\rightarrow 1\pi$ Solution

$\lim_x\rightarrow 2x$ Solution

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Exemple

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Solution

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Solution

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Solution

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Exemple

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Solution

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Cas 1: Limite d'une puissance X

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Solution

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Les références