Somme de propriété associative, multiplication, exemples, exercices

La propriété associative de la somme représente la nature associative de l'opération ajoute divers ensembles mathématiques. Il rapporte trois (ou plus) éléments de ces ensembles, appelés A, B et C, de sorte qu'il est toujours accompli:

a + (b + c) = (a + b) + c

De cette façon, il est garanti que, quelle que soit la façon de se regrouper pour effectuer l'opération, le résultat est le même.

Figure 1. Nous utilisons à plusieurs reprises la propriété associative de la somme lorsque vous effectuez des opérations arithmétiques et algébriques. (Dessin: Freepik Composition: F. Zapata)

Mais il convient de noter que la propriété associative n'est pas synonyme de propriété commutative. C'est-à-dire que nous savons que l'ordre des addeds ne modifie pas la somme ou que l'ordre des facteurs ne modifie pas le produit. Donc pour la somme que vous pouvez écrire comme ceci: a + b = b + a.

Cependant, dans la propriété associative, elle est différente, car l'ordre des éléments à ajouter est maintenu et les modifications est l'opération qui est exécutée en premier. Ce qui signifie que cela n'a pas d'importance en premier (b + c) et à ce résultat ajouter à, pour commencer à ajouter à b et au résultat ajouter c.

De nombreuses opérations importantes telles que la somme sont associatives, mais pas toutes. Par exemple, dans la soustraction de nombres réels, il se produit que:

A - (b - c) ≠ (a - b) - c

Oui a = 2, b = 3, c = 1, alors:

2- (3 - 1) ≠ (2 - 3) - 1

0 ≠ -2

[TOC]

Propriété associative de la multiplication

Comme cela a été fait pour la somme, la propriété associative de la multiplication indique que:

a ˟ (b ˟ c) = (a ˟ b) ˟ c

Peut vous servir: somme des polynômes, comme cela est fait, des exemples, des exercices

Dans le cas de l'ensemble des nombres réels, il est facile de vérifier qu'il est toujours. Par exemple, en utilisant les valeurs a = 2, b = 3, c = 1, vous devez:

2 _˟ (3 _˟ 1) = (2 _˟  3) _˟ 1 → 2 _˟ 3 = 6 _˟ 1

6 = 6

Les nombres réels répondent à la propriété associative de la somme et de la multiplication. D'un autre côté, dans un autre ensemble, comme celui des vecteurs, la somme est associative, mais le produit transversal ou le produit vectoriel n'est pas.

Applications de la propriété associative de la multiplication

Un avantage que les opérations dans lesquelles la propriété associative est remplie doit regrouper de la manière la plus pratique. Cela facilite considérablement la résolution.

Par exemple, supposons que dans une petite bibliothèque, il y a 3 étagères avec 5 divertissements chacun. Dans chaque divertissement, il y a 8 livres. Combien de livres sont en total?

Nous pouvons effectuer l'opération comme suit: Livres totaux = (3 x 5) x 8 = 15 x 8 = 120 livres.

En outre: 3 x (5 x 8) = 3 x 40 = 120 livres.

Figure 2. Une application de la propriété associative de la multiplication consiste à calculer le nombre de livres sur chaque étagère. Image créée par f. Zapata.

Exemples

-Dans les ensembles de nombres naturels, entiers, rationnels, réels et complexes, la propriété associative de la somme et de la multiplication est remplie.

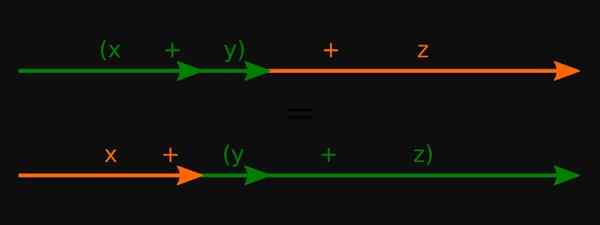figure 3. Pour les nombres réels, la propriété associative de la somme est remplie. Source: Wikimedia Commons.

-Pour les polynômes, ils s'appliquent également dans ces opérations.

-En cas d'opérations de soustraction, de division et d'exponentiation, les biens associatifs ne sont pas remplis en nombre réel ou polynôme.

Peut vous servir: Orthoedro: formules, zone, volume, diagonale, exemples

-Dans le cas des matrices, la propriété associative est remplie pour la somme et la multiplication, bien que dans ce dernier cas, la commuttivité ne soit pas respectée. Cela signifie que, compte tenu des matrices A, B et C, il est vrai que:

(A x b) x c = a x (b x c)

Mais ... a x b ≠ b x a

Propriété associative chez les vecteurs

Les vecteurs forment un ensemble différent des nombres réels ou des nombres complexes. Les opérations définies pour l'ensemble des vecteurs sont quelque peu différentes: il y a une somme, une soustraction et trois types de produits.

La somme des vecteurs rencontre la propriété associative, ainsi que les nombres, les polynômes et les matrices. Quant aux produits scalaires, grimpant par vecteur et croix fabriqués entre les vecteurs, ce dernier ne se rencontre pas, mais le produit scalaire, qui est un autre type de fonctionnement entre les vecteurs, le remplit, en tenant compte de ce qui suit:

-Le produit d'un scalaire pour un vecteur se traduit par un vecteur.

-Et en grimpant deux vecteurs, c'est un scalaire.

Par conséquent, étant donné les vecteurs V, ou et W, Et en outre un scalaire λ, il est possible d'écrire:

-Somme des vecteurs: V +(ou + W ) = (V + ou) + W

-Produit scalaire: λ (V • ou ) = (λV) • ou

Ce dernier est possible grâce à ce V • ou C'est un scalaire, et λV C'est un vecteur.

Cependant:

V × (ou × W ) ≠ (V × ou)×W

Factorisation polynomiale en regroupant les termes

Cette application est très intéressante, car comme indiqué ci-dessus, une propriété associative aide à résoudre certains problèmes. La somme des monomiaux est associative et cela peut être utilisé pour prendre en compte lorsqu'un facteur commun évident n'apparaît pas à première vue.

Peut vous servir: polygone convexe: définition, éléments, propriétés, exemples

Par exemple, supposons qu'il est demandé de prendre en compte: X³ + 2X² + 3X +6. Ce polynôme n'a pas de facteur commun, mais voyons ce qui se passe s'il est regroupé de cette manière:

X³ + 2x² + 3x +6 = (x³ + 2x²) + (3x +6)

La première parenthèse a un facteur commun X²:

X³ + 2X² = X² (x + 2)

Dans le second, le facteur commun est de 3:

3x +6 = 3 (x + 2)

Ensuite:

X³ + 2X² + 3X +6 = X²(x + 2) + 3 (x + 2)

Maintenant, il y a un facteur commun évident, qui est x + 2:

X²(x + 2) + 3 (x + 2) = (x + 2) (x²+3)

Exercices

- Exercice 1

La construction d'une école a 4 étages et dans chacun il y a 12 salles de classe avec 30 bureaux à l'intérieur. Combien de bureaux de l'école a-t-il au total?

Solution

Ce problème est résolu en appliquant la propriété associative de la multiplication, voyons:

Nombre total de bureaux = 4 étages x 12 salles de classe / plancher x 30 bureaux / salle de classe = (4 x 12) x 30 bureaux = 48 x 30 = 1440 bureaux.

O Si préféré: 4 x (12 x 30) = 4 x 360 = 1440 bureaux

- Exercice 2

Compte tenu des polynômes:

A (x) = 5x³ + 2x² -7x + 1

B (x) = x⁴ +6x³ -5x

C (x) = -8x² +3x -7

Appliquer la propriété associative de la somme pour trouver (x) + b (x) + c (x).

Solution

Les deux premiers peuvent être regroupés et le résultat ajoute le troisième:

A (x) + b (x) = [5x³ + 2x² -7x + 1] + [x⁴ +6x³ -5x] = x⁴ + 11x³+ 2x² -12x +1

Le polynôme C (x) est immédiatement ajouté:

[X⁴ + 11x³+ 2x² -12x +1] + [-8x² +3x -7] = x⁴ + 11x³ - 6x² -9x -6

Le lecteur peut vérifier que le résultat est identique s'il est résolu par l'option A (x) + [b (x) + c (x)]].

Les références

1. Jiménez, R. 2008. Algèbre. Prentice Hall.
2. Les mathématiques sont amusantes. Lois commutatives, associatives et de district. Récupéré de: Mathisfun.com.
3. Entrepôt de mathématiques. Définition de la propriété associative. Récupéré de: Mathwarehouse.com.
4. Science. Propriété associative et commutative de l'addition et de la multiplication (avec exemple). Récupéré de: science.com.
5. Wikipédia. Propriété associative. Récupéré de: dans.Wikipédia.org.