Programmation linéaire à quoi sert, modèles, restrictions, applications

La programmation linéaire Il s'agit d'une méthode mathématique qui sert à optimiser (maximiser ou minimiser le requis) une fonction dont les variables sont soumises à des restrictions, tant que la fonction et les restrictions dépendent linéairement des variables.

Généralement, la fonction pour optimiser une situation pratique, comme le gain d'un fabricant dont les intrants, la main-d'œuvre ou les machines sont limités.

Figure 1. La programmation linéaire est largement utilisée pour optimiser les bénéfices. Source: piqsels.

L'un des cas les plus simples est celui d'une fonction linéaire à maximiser, qui ne dépend que de deux variables, appelées Variables de décision. Il peut être forme:

Z = k₁x + k₂et

Avec k₁ et K₂ constantes. Cette fonction est connue sous le nom de Fonction objective. Bien sûr, il existe des situations qui méritent plus de deux variables pour leur étude, étant plus complexe:

Z = k₁X₁ + k₂X₂ + k₃X₃ +.. .

Et les restrictions sont également modélisées mathématiquement par un système d'équations ou d'inégations, également linéaire X et et.

L'ensemble des solutions de ce système est appelé solutions réalisables soit points réalisables. Et parmi les points réalisables, il y en a au moins un, qui optimise la fonction objectif.

La programmation linéaire a été développée indépendamment par le physicien et mathématicien américain.

La méthode de résolution de problèmes connue sous le nom Méthode simplex C'est la création de Dantzig, qui a travaillé pour l'US Air Force, l'Université de Berkeley et l'Université de Stanford.

Figure 2. Les mathématiciens George Dantzig (à gauche) et Leonid Kantorovich (à droite). Source: F. Zapata.

[TOC]

Modèles de programmation linéaire

Les éléments nécessaires pour établir un modèle de programmation linéaire, approprié à une situation pratique, sont:

-Fonction objective

-Variables de décision

-Restrictions

Dans la fonction objectif, ce que vous voulez réaliser est défini. Par exemple, supposons qu'il est souhaité de maximiser les bénéfices obtenus à partir de la fabrication de certains produits. Ensuite, la fonction «bénéfice» est établie, selon le prix auquel les produits sont vendus.

En termes mathématiques, cette fonction peut être exprimée abrégée en utilisant la somme:

Z = ∑k_Toi X_Toi

Dans cette équation, k_Toi Ce sont des coefficients et x_Toi sont les variables de décision.

Les variables de décision sont les éléments du système dont le contrôle est et leurs valeurs sont des nombres réels positifs. Dans l'exemple proposé, les variables de décision sont la quantité de chaque produit à fabriquer pour obtenir le gain maximal.

Enfin, nous avons les restrictions, qui sont des équations linéaires ou des inégalités en termes de variables de décision. Ils décrivent les limites du problème, qui sont connues et peuvent être par exemple les quantités de matières premières disponibles dans la fabrication.

Peut vous servir: fonctions supérieures à deux (exemples)

Types de restrictions

Vous pouvez avoir un montant M de limitations, à partir de J = 1 jusqu'à J = m. Mathématiquement, les restrictions sont de trois types:

1. POUR_J = ∑ a_ij . X_Toi
2. B_J ≥ ∑ b_ij . X_Toi
3. C_J ≤ ∑ c_ij . X_Toi

La première restriction est du type d'équation linéaire et signifie que la valeur_J, qui est connu, doit être respecté.

Les deux restrictions restantes sont des inégations linéaires et signifie que les valeurs B_J et C_J, connu, peut être respecté ou surmonté, lorsque le symbole qui apparaît est ≥ (plus grand ou égal à) ou le respect ou non, si le symbole est ≤ (inférieur ou égal à).

Exemple de modèle

Les champs d'application sont très divers, couvrant de l'administration des affaires à la nutrition, mais pour comprendre la méthode, un modèle simple d'une situation pratique avec deux variables est ensuite proposé.

Une pâtisserie locale est connue pour deux spécialités: le gâteau de la jungle noire et le gâteau de la sacrista.

Dans son élaboration, ils nécessitent des œufs et du sucre. Pour la jungle noire, 9 œufs et 500 g de sucre sont nécessaires, tandis que 8 œufs et 800 g de sucre sont nécessaires pour la sacrénine. Les prix de vente respectifs sont de 8 $ et 10.

Le problème est: le nombre de gâteaux de chaque type que la pâtisserie doit faire pour maximiser son gain, sachant qu'il a 10 kilos de sucre et 144 œufs?

Variables de décision

Les variables de décision sont "x" et "y", qui prennent des valeurs réelles:

-X: la quantité de gâteaux de jungle noire

-Y: gâteaux de type sacriphantine.

Restrictions

Les restrictions sont données par le fait que le nombre de gâteaux est un montant positif et qu'il y a des quantités limitées de matières premières pour les préparer.

Par conséquent, de manière mathématique, ces restrictions acquièrent le formulaire:

1. x ≥ 0
2. et ≥0
3. 9x + 8y ≤ 144
4. 0.5 x + 0.8 et ≤ 10

Les restrictions 1 et 2 constituent le Condition non négative précédemment exposé, et toutes les inégations soulevées sont linéaires. Dans les restrictions 3 et 4 sont les valeurs qui ne doivent pas être surmontées: 144 œufs et 10 kg de sucre.

Fonction objective

Enfin, la fonction objective est le gain obtenu par la fabrication de «x» de gâteaux de jungle noire plus la quantité «y» de sacristines. Il est construit en multipliquant le prix par la quantité de gâteaux fabriqués et en ajoutant pour chaque type. C'est une fonction linéaire que nous appellerons g (x, y):

G = 8x + 10y

Méthodes de solution

Parmi les différentes méthodologies de solution figurent des méthodes graphiques, l'algorithme simplex et la méthode du point interne, pour en mentionner certains.

- Méthode graphique ou géométrique

Lorsque vous avez un problème de deux variables telles que la section précédente, les restrictions déterminent une région polygonale dans le plan Xy, appel Région possible soit Région de viabilité.

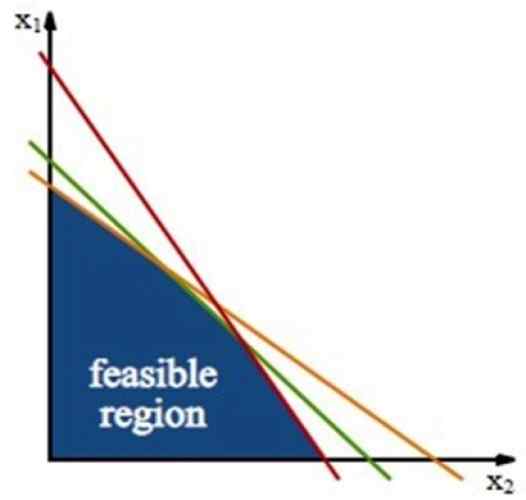figure 3. La région réalisable, où se trouve la solution du problème d'optimisation. Source: Wikimedia Commons.

Cette région est construite à travers Lignes de restriction, qui sont les lignes obtenues à partir des inégations des restrictions, travaillant uniquement avec le signe de l'égalité.

Peut vous servir: ensemble fini: propriétés, exemples, exercices résolus

Dans le cas de la boulangerie qui souhaite optimiser les bénéfices, les lignes de restriction sont:

1. x = 0
2. y = 0
3. 9x + 8y = 144
4. 0.5 x + 0.8y = 10

Tous les points de la région verrouillés par ces lignes sont des solutions possibles, donc il y en a infini. Sauf dans le cas où la région réalisable est vide, auquel cas le problème soulevé n'a pas de solution.

Heureusement, pour le problème de pâtisserie, la région réalisable n'est pas vide, nous l'avons ci-dessous.

Figure 4. La région réalisable du problème de la pâte. La ligne droite 0 traverse l'origine. Source: F. Zapata avec Geogebra.

La solution optimale, si elle existe, est à l'aide de la fonction objectif. Par exemple, lorsqu'il s'agit de trouver le gain G maximum, vous avez la ligne suivante, qui est appelée Iso-beneenfice droit:

G = k₁x + k₂et → y = -k₁x / k₂ + G / k₂

Avec cette ligne, toutes les paires (x, y) sont obtenues qui fournissent un gain donné G, il y a donc une famille de lignes en fonction de la valeur de G, mais tout avec la même pente -k₁ / k₂, afin qu'ils soient parallèles directement.

La solution optimale

Maintenant, il peut être démontré que la solution optimale d'un problème linéaire est toujours un extrême ou un sommet de la région réalisable. Ensuite:

La solution de ligne est la plus éloignée de l'origine et qui a au moins un point en commun avec la région réalisable.

Si la ligne la plus proche de l'origine a un segment entier en commun avec la région réalisable, il est dit qu'il existe des solutions infinies. Ce cas se produit si la pente de la ligne des iso-avantages est égale à celle de l'une des autres lignes qui limitent la région.

Pour notre pâtisserie, les sommets candidats sont A, B et C.

- Méthode simplex de Dantzig

La méthode graphique ou géométrique est applicable à deux variables. Cependant, il est plus compliqué lorsqu'il existe trois variables et impossible à utiliser pour un plus grand nombre de variables.

En ce qui concerne les problèmes de plus de deux variables, le Méthode simplex, qui consiste en une série d'algorithmes pour optimiser les fonctions objectives. Les matrices simples et l'arithmétique sont généralement utilisées pour effectuer les calculs.

La méthode simplex commence par choisir une solution réalisable et vérifier si elle est optimale. Si c'est le cas, nous avons déjà résolu le problème, mais si ce n'est pas le cas, il continue vers une solution plus proche de l'optimisation. Si la solution existe, l'algorithme avec lui en quelques tentatives.

Peut vous servir: quelle est la gamme de statistiques? (Avec des exemples)

Applications

Programmation linéaire et non linéaire appliquée dans de nombreux domaines pour prendre les meilleures décisions pour réduire les coûts et augmenter les bénéfices, qui ne sont pas toujours monétaires, car ils peuvent être mesurés à temps, par exemple, si vous cherchez à minimiser le temps nécessaire pour effectuer une série d'opérations.

Voici quelques champs:

-En marketing, il est utilisé pour trouver la meilleure combinaison de médias (réseaux sociaux, télévision, presse et autres) pour annoncer un certain produit.

-Pour l'allocation des travaux appropriés au personnel d'une entreprise ou d'une usine ou des horaires.

-Dans la sélection des aliments les plus nutritifs et au plus bas coût des industries de l'élevage et de la volaille.

Exercices résolus

- Exercice 1

Graphiquement le modèle de programmation linéaire soulevé dans les sections précédentes.

Solution

Il est nécessaire de représenter graphiquement l'ensemble des valeurs déterminées par le système de restrictions spécifié dans le problème:

1. x ≥ 0
2. et ≥0
3. 9x + 8y ≤ 144
4. 0.5 x + 0.8 et ≤ 10

La région donnée par les inégations 1 et 2 correspond au premier quadrant du plan cartésien. Quant aux inégations 3 et 4, il commence par trouver les lignes de restriction:

9x + 8y = 144

0.5 x + 0.8y = 10 → 5x + 8y = 100

La région possible est un quadrilatère dont les sommets sont des points A, B, C et D.

Le gain minimum est de 0, donc la ligne 8x + 10 et 10 est la limite inférieure et les lignes ISO -Benefit ont en attente -8/10 = -0.8.

Cette valeur est différente des pentes des autres lignes de restriction et comme la région possible est limitée, il y a la solution unique.

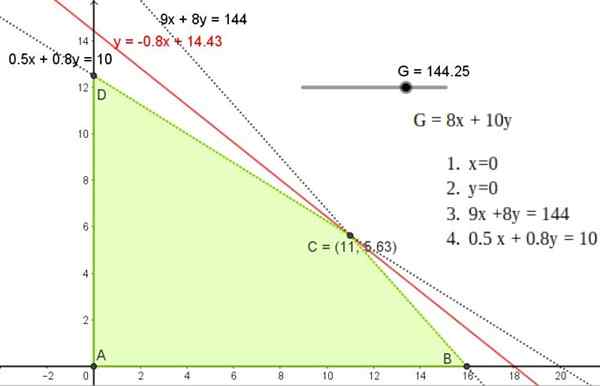Figure 5. Solution graphique de l'exercice 1, montrant la région réalisable et la solution ponctuelle C dans l'un des sommets de ladite région. Source: F. Zapata.

Cette solution correspond à une ligne de pente -0.8 qui passe par l'un des points A, B ou C, dont les coordonnées sont:

A (11; 5.625)

B (0; 12.5)

C (16, 0)

Solution optimale

Nous calculons la valeur de G pour chacun de ces points:

-(11; 5.625): G_POUR = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): G_B = 8 x 0 + 10 x 12.5 = 125

-(16, 0): g_C = 8 x 16 + 10 x 0 = 128

Le plus gros gain consiste à fabriquer 11 gâteaux de jungle noire et 5.625 gâteaux sacripantins. Cette solution est d'accord avec celui trouvé via le logiciel.

- Exercice 2

Vérifiez le résultat de l'exercice précédent en utilisant la fonction Solver (Sololer) disponible dans la plupart des feuilles de calcul telles que Excel ou Calc de LibreOffice, qui intègrent l'algorithme simplex pour l'optimisation de programmation linéaire.

Solution

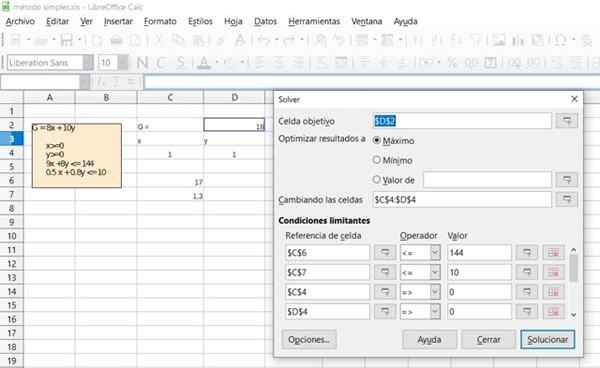Figure 6. Détail de la solution de l'exercice 1 via la feuille de calcul gratuite de calcul du bureau. Source: F. Zapata. 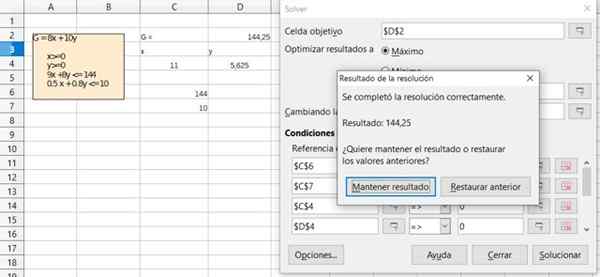Figure 7. Détail de la solution de l'exercice 1 via la feuille de calcul gratuite de calcul du bureau. Source: F. Zapata.

Les références

1. Brillant. Programmation linéaire. Récupéré de: brillant.org.
2. Eppen, G. 2000. Recherche opérationnelle en sciences administratives. 5e. Édition. Prentice Hall.
3. Haeussler, e. 1992. Mathématiques pour l'administration et l'économie. 2e. Édition. Groupe éditorial ibero-américain.
4. Hiru.EUS. Programmation linéaire. Récupéré de: Hiru.EUS.
5. Wikipédia. Programmation linéaire. Récupéré de: est. Wikipédia.org.