Produits remarquables

Quels sont les produits notables?

Les produits notables sont des opérations algébriques, où les multiplications des polynômes sont exprimées, qui n'ont pas besoin d'être traditionnellement résolues, mais à l'aide de certaines règles, les résultats de la même chose peuvent être trouvés.

Les polynômes sont multipliés par la question de savoir si, par conséquent, il est possible qu'ils aient beaucoup de termes et de variables. Pour rendre le processus court, les règles des produits notables sont utilisées, qui permettent des multiplications sans avoir à aller pour terme.

Produits et exemples notables

Chaque produit remarquable est une formule qui résulte d'une factorisation, composée de polynômes de plusieurs termes tels que des binômes ou des trinomiaux, appelés facteurs.

Les facteurs sont à la base d'une puissance et ont un exposant. Lorsque les facteurs se multiplient, les exposants doivent être ajoutés.

Il existe plusieurs formules de produits notables, certaines sont plus utilisées que d'autres, selon les polynômes, et sont les suivantes:

Binôme carré

Il s'agit de la multiplication d'un binôme en soi, exprimé sous forme de pouvoir, où les termes sont ajoutés ou soustraits:

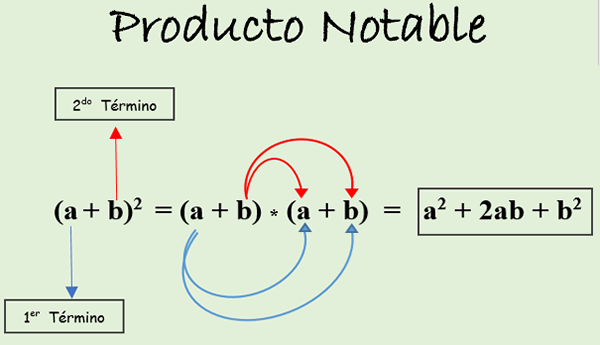
pour. Binôme de somme carrée: Il est égal au carré du premier terme, plus le double du produit des termes, plus le carré du deuxième terme. Il est exprimé comme suit:

(A + B)² = (a + b) _* (A + B).

Dans la figure suivante, vous pouvez voir comment le produit est développé en fonction de la règle susmentionnée. Le résultat est appelé trinomial d'un carré parfait.

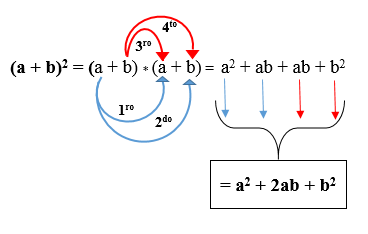
Exemple 1

(x + 5) ² = x² + 2 (x * 5) + 5²

(x + 5) ² = x² + 2 (5x) + 25

(x + 5) ² = x² + 10x + 25.

Exemple 2

(4a + 2b) = (4a)² + 2 (4e _* 2b) + (2b)²

(4a + 2b) = 8a² + 2 (8ab) + 4b²

(4a + 2b) = 8a² + 16 AB + 4B².

b. Binôme d'une soustraction carrée: La même règle du binôme d'une somme est appliquée, seulement que dans ce cas le deuxième terme est négatif. Sa formule est la suivante:

(UN B)² = [(a) + (- b)]²

Peut vous servir: analogies numériques: types, applications et exercices

(UN B)² = A² +2e _* (-b) + (-b)²

(UN B)²   = A² - 2AB + B².

Exemple 1

(2x - 6)² = (2x)² - 2 (2x _* 6) + 6²

(2x - 6)²  = 4x² - 2 (12x) + 36

(2x - 6)² = 4x² - 24x + 36.

Produit des binômes conjugués

Deux binômes sont conjugués lorsque les deuxième termes de chacun sont de signes différents, c'est-à-dire celui du premier est positif et celui du deuxième négatif ou vice versa. Il est résolu en élevant chaque carré monomial et soustrait. Sa formule est la suivante:

(A + B) _* (UN B)

Dans la figure suivante, le produit de deux binômes conjugués est développé, où il est observé que le résultat est une différence de carrés.

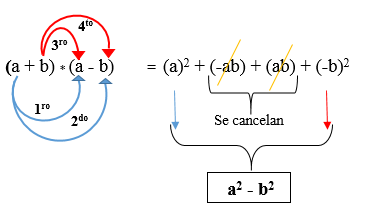
Exemple 1

(2a + 3b) (2a - 3b) = 4a² + (-6ab) + (6 ab) + (-9b²)

(2a + 3b) (2a - 3b) = 4a² - 9b².

Produit de deux binômes avec un terme commun

C'est l'un des produits notables les plus complexes et les plus utilisés car il s'agit d'une multiplication de deux binômes qui ont un terme commun. La règle indique ce qui suit:

• Le carré du terme commun.
• Plus la somme les termes qui ne sont pas communs puis les multiplier par le terme commun.
• Plus la somme de la multiplication des termes qui ne sont pas communs.

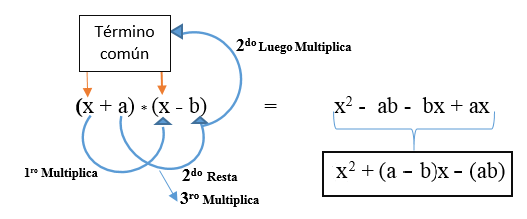
Il est représenté dans la formule: (x + a) _* (x + b) et est développé comme indiqué dans l'image. Le résultat est un trinôme carré non parfait.

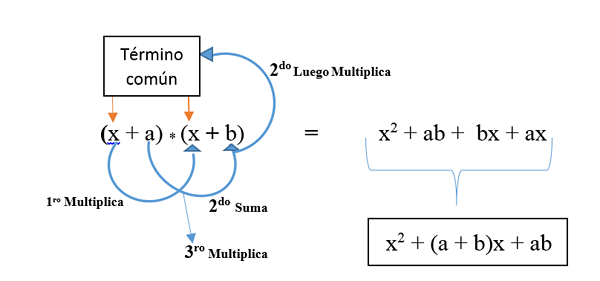Exemple 1

(x + 6) _* (x + 9) = x² + (6 + 9) _* X + (6 _* 9)

(x + 6) _* (x + 9) = x² + 15x + 54.

Il est possible que le deuxième terme (le terme différent) soit négatif et sa formule est la suivante: (x + a) _* (x - b).

Exemple 2

(7x + 4) _* (7x - 2) = (7x _* 7x) + (4 - 2)_* 7x + (4 _* -2)

(7x + 4) _* (7x - 2) = 49x² + (2)_* 7x - 8

(7x + 4) _* (7x - 2) = 49x² + 14x - 8.

Il peut également être le cas que les deux termes différents sont négatifs. Votre formule sera: (x - a) _* (x - b).

Peut vous servir: Théorème de Lamy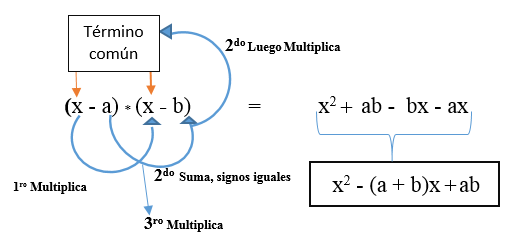

Exemple 3

(3b - 6) _* (3b - 5) = (3b _* 3b) + (-6 - 5)_* (3b) + (-6 _* -5)

(3b - 6) _* (3b - 5) = 9b² + (-onze) _* (3b) + (30)

(3b - 6) _* (3b - 5) = 9b² - 33b + 30.

Polynôme carré

Dans ce cas, il y a plus de deux termes et pour le développer, chacun est coupé et ajoute avec deux fois la multiplication d'un terme avec un autre; Sa formule est: (a + b + c)² Et le résultat de l'opération est un carré trinomial.

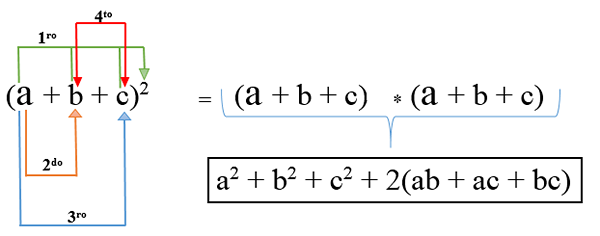
Exemple 1

(3x + 2y + 4z)² = (3x)² + (2 et)² + (4Z)² + 2 (6xy + 12xz + 8yz)

(3x + 2y + 4z)² = 9x² + 4Y² + 16Z² + 12xy + 24xz + 16Yz.

Cube binomial

C'est un produit notable complexe. Pour le développer, le binomial est multiplié par son carré, comme suit:

pour. Pour le binôme au cube d'une somme:

• Le cube du premier terme, plus triple sur le carré du premier terme par le second.
• Plus triple le premier terme, par le deuxième carré.
• Plus le cube du deuxième mandat.

(A + B)³ = (a + b) _* (A + B)²

(A + B)³ = (a + b) _* (pour² + 2AB + B²)

(A + B)³ = A³ + 2e²B + ab² + ba² + 2AB² + b³

(A + B)³ = A³ + 3e²B + 3AB² + b³.

Exemple 1

(A + 3)³ = A³ + 3 (a)²_*(3) + 3 (a)_*(3)² + (3)³

(A + 3)³ = A³ + 3 (a)²_*(3) + 3 (a)_*(9) + 27

(A + 3)³ = A³ + 9 A² + 27a + 27.

b. Pour le binôme au cube d'une soustraction:

• Le cube du premier terme, à l'exception du triple du carré du premier terme par le second.
• Plus triple le premier terme, par le deuxième carré.
• Moins le cube du deuxième terme.

(UN B)³ = (a - b) _* (UN B)²

(UN B)³ = (a - b) _* (pour² - 2AB + B²)

(UN B)³ = A³ - 2e²B + ab² - ba² + 2AB² - b³

(UN B)³ = pour³ - 3e²B + 3AB² - b³.

Exemple 2

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(-5)² + (-5)³

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(25) -125

Peut vous servir: données non groupées: exemples et exercice résolus

(B - 5)³ = b³ - 15B² +75b - 125.

Cube trinomial

Il développe le multiplier par son carré. C'est un produit remarquable très étendu car il y a 3 termes soulevés sur le cube, plus le triple de chaque terme carré, multiplié par chacun des termes, plus six fois le produit des trois termes. Vu sous une meilleure forme:

(A + B + C)³ = (A + b + c) _* (A + B + C)²

(A + B + C)³ = (A + b + c) _* (pour² + b² + c² + 2AB + 2AC + 2BC)

(A + B + C)³ = A³ + b³ + c³ + 3e²B + 3AB² + 3e²C + 3AC² + 3B²C + 3BC² + 6abc.

Exemple 1

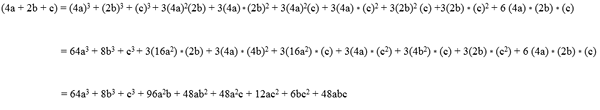
Exercices résolus de produits notables

Exercice 1

Développer le binôme suivant au cube: (4x - 6)³.

Solution

Rappelant qu'un binôme du cube est égal au premier terme levé au cube, à l'exception du triple du carré du premier terme par le second; plus triple le premier terme, par le deuxième carré, à l'exception du cube du deuxième terme.

(4x - 6)³ = (4x)³ - 3 (4x)²(6) + 3 (4x) _* (6)² - (6)²

(4x - 6)³ = 64x³ - 3 (16x²) (6) + 3 (4x)_* (36) - 36

(4x - 6)³ = 64x³ - 288x² + 432x - 36.

Exercice 2

Développer le binôme suivant: (x + 3) (x + 8).

Solution

Vous avez un binôme où il y a un terme commun, qui est x et le deuxième terme est positif. Pour le développer, seul le terme commun doit être augmenté, plus la somme des termes qui ne sont pas communs (3 et 8), puis les multiplier par le terme commun, plus la somme de la multiplication des termes qui ne sont pas communs.

(x + 3) (x + 8) = x² + (3 + 8) x + (3_*8)

(x + 3) (x + 8) = x² + 11x + 24.

Les références

1. Angel, un. R. (2007). Algèbre élémentaire. Pearson Education,.
2. Arthur Goodman, L. H. ( mille neuf cent quatre vingt seize). Algèbre et trigonométrie avec géométrie analytique. Pearson Education.
3. Das, s. (s.F.). Maths plus 8. Royaume-Uni: Sagar Ratna.
4. Jerome E. Kaufmann, k. L. (2011). Algèbre élémentaire et intermédiaire: une approche combinée. Floride: Cengage Learning.
5. Pérez, C. D. (2010). Pearson Education.