Concept de probabilité de fréquence, comment est calculé et des exemples

La La probabilité de fréquence est une sous-définition dans l'étude de la probabilité et de ses phénomènes. Sa méthode d'étude en ce qui concerne les événements et les attributs, est basé sur de grandes quantités d'itérations, observant ainsi chacun à long terme ou même aux répétitions infinies.

Par exemple, une enveloppe gummitan contient 5 caoutchoucs de chaque couleur: bleu, rouge, vert et jaune. Vous souhaitez déterminer la probabilité que chaque couleur doit partir après une sélection aléatoire.

Source: Pexels

Il est fastidieux d'imaginer obtenir un caoutchouc, l'enregistrer, le retourner, éliminer un caoutchouc et répéter les mêmes centaines ou plusieurs milliers de fois. Vous pouvez même vouloir observer le comportement après plusieurs millions d'itérations.

Mais au contraire, il est intéressant de découvrir, qu'après quelques répétitions, la probabilité attendue de 25% n'est pas entièrement remplie, du moins pas pour toutes les couleurs après 100 itérations.

En vertu de l'approche de probabilité de fréquence, l'allocation des valeurs ne se produira que par l'étude de nombreuses itérations. De cette façon, le processus doit être effectué et de préférence enregistré de manière informatisée ou émulée.

Les courants multiples rejettent la probabilité de fréquence, arguant un manque d'empirisme et de fiabilité dans les critères aléatoires.

[TOC]

Comment la probabilité de fréquence est-elle calculée?

Lors de la programmation de l'expérience dans n'importe quelle interface capable d'offrir une itération purement aléatoire, vous pouvez commencer à étudier la probabilité de fréquence du phénomène à travers un tableau de valeurs.

L'exemple précédent est apprécié de l'approche de fréquence:

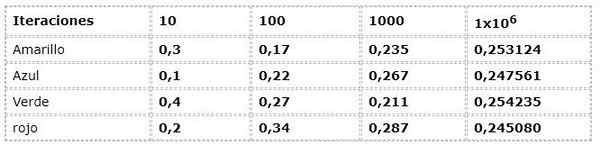
Les données numériques correspondent à l'expression:

N (a) = nombre d'occurrences / nombre d'itérations

Où n (a) représente la fréquence relative de l'événement «A»

«A» appartient à l'ensemble des résultats possibles ou de l'espace d'échantillon Ω

Il peut vous servir: Multiples of 8: Que sont et explications

Ω: rouge, vert, bleu, jaune

Il y a une dispersion considérable dans les premières itérations, lorsque des fréquences avec jusqu'à 30% des différences sont observées les unes avec les autres, ce qui est un fait très élevé pour une expérience qui a théoriquement des événements avec la même possibilité (équivoque).

Mais à mesure que les itérations augmentent, les valeurs semblent de plus en plus à celles présentées par le courant théorique et logique.

Loi des grands nombres

En tant qu'accord inattendu entre les approches théoriques et fréquentes, la loi d'un grand nombre survient. Lorsqu'il est établi qu'après une quantité considérable d'itérations, les valeurs de l'expérience de fréquence approchent des valeurs théoriques.

Dans l'exemple, vous pouvez remarquer comment les valeurs sont approximées à 0,250 à mesure que les itérations augmentent. Ce phénomène est élémentaire dans les conclusions de nombreuses œuvres probabilistes.

Source: Pexels

Autres approches de probabilité

Il existe 2 autres théories ou approches de la notion de probabilité en plus du Probabilité de fréquence.

Théorie logique

Votre approche est orientée vers la logique déductive des phénomènes. Dans l'exemple précédent, la probabilité d'obtenir chaque couleur est fermée à 25%. Autrement dit.

Théorie subjective

Il est basé sur les connaissances et les croyances antérieures que chaque individu a sur les phénomènes et les attributs. Des déclarations comme "Il pleut toujours dans la semaine sainte " Ils obéissent à un modèle d'événements similaires qui se sont produits auparavant.

Histoire

Les débuts de sa mise en œuvre datent du XIXe siècle, lorsque je l'ai cité dans plusieurs de ses travaux à Cambridge England. Mais ce n'est que le XXe siècle que 2 mathématiques statistiques ont développé et façonné le Probabilité de fréquence.

Peut vous servir: équations polynomiales

L'un d'eux était Hans Reichenbach, qui développe son travail dans des publications telles que "Theory of Probability" publiée en 1949.

L'autre était Richard Von Mises, qui a développé son travail plus approfondie à travers plusieurs publications et a proposé de considérer la probabilité comme une science mathématique. Ce concept était nouveau en mathématiques et marquerait le début d'une ère de croissance dans l'étude de la Probabilité de fréquence.

En fait, cet événement fait la seule différence avec les contributions apportées par la génération de Venn, Counot et Helm. Où la probabilité devient un homologue comme la géométrie et la mécanique.

< La teoría de las probabilidades trata con phénomènes massifs et événements répétitifs. Des problèmes dans lesquels le même événement est répété encore et encore, ou un grand nombre d'éléments uniformes sont impliqués en même temps> Richard von Mises

Phénomènes massifs et événements répétitifs

Trois types peuvent être classés:

• Physique: modèles d'obdose de la nature au-delà d'une condition aléatoire. Par exemple le comportement des molécules d'un élément dans un échantillon.
• Chance: sa considération fondamentale est le hasard, comme en libérant un dés à plusieurs reprises.
• Statistiques biologiques: sélections de sujets en fonction de leurs caractéristiques et attributs.

Dans la théorie, l'individu qui mesure joue un rôle dans les données probabilistes, car ce sont ses connaissances et ses expériences qui articulent cette valeur ou cette prédiction.

Dans la Probabilité de fréquence Les événements seront considérés comme des collections à traiter, où l'individu ne joue aucun rôle dans l'estimation.

Les attributs

Dans chaque élément, un attribut se produit, qui sera variable en fonction de la nature de ce. Par exemple, dans le type de phénomène physique, les molécules d'eau auront des vitesses différentes.

Il peut vous servir: critères de similitude triangulaire

Dans le lancement des dés, nous connaissons l'espace d'échantillon ω qui représente les attributs de l'expérience.

Ω: 1, 2, 3, 4, 5, 6

Il y a d'autres attributs tels que Ω_P  ou être bizarre ω_Toi

Ω_p : 2, 4, 6

Ω_Toi : 1, 3, 5

Qui peut être défini comme des attributs non élémentaires.

Exemple

• Vous souhaitez calculer la fréquence de chaque somme possible dans le lancement de deux dés.

Pour cela, une expérience est programmée où deux valeurs aléatoires entre [1, 6] sont ajoutées dans chaque itération.

Les données sont enregistrées dans un tableau et les tendances en grand nombre sont étudiées.

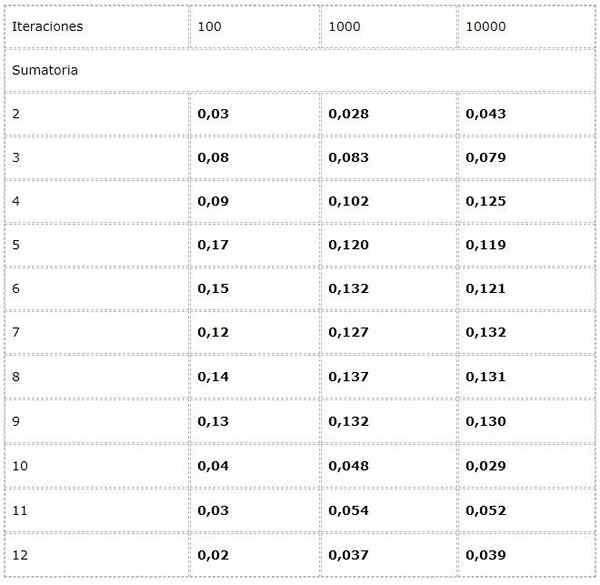
Il est observé que les résultats peuvent varier considérablement entre les itérations. Cependant, la loi de grands nombres peut être observée dans la convergence apparente présentée dans les deux dernières colonnes.

Les références

1. Statistiques et évaluation des preuves des médecins légistes. Deuxième édition. Colin G.g. Aitken. École des mathématiques. Université d'Édimbourg, Royaume-Uni
2. Mathématiques pour l'informatique. Eric Lehman. Google Inc.
   F Thomson Leighton Department of Mathematics and the Computer Science and AI Laboratory, Massachussetts Institute of Technology; Akamai Technologies
3. The Arithmétique Professeur, Volume 29. Conseil national des enseignants des mathématiques, 1981. Université du Michigan.
4. Théorie des nombres d'apprentissage et d'enseignement: Recherche en cognition et instruction / édité par Stephen R. Campbell et Rina Zazkis. Ablex Publishing 88 Post Road West, Westport CT 06881
5. Bernoulli, J. (1987). Ars conjectandi- 4ème partitie. Rouen: Irem.