Caractéristiques du prisme pentagonal, parties, sommets, bords, volume

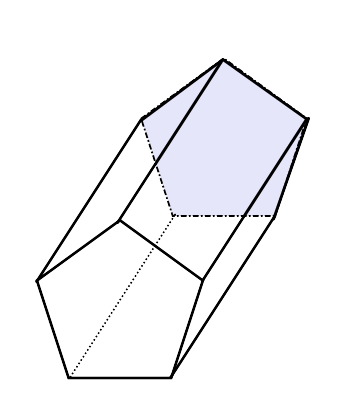
UN Prisme pentagonal Il s'agit d'une figure géométrique à trois dimensions dont les bases, identiques, ont une forme de pentagone, et ont également un total de 5-tasses sous forme de parallélogramme.

Si les visages sont rectangulaires, il est dit que c'est un Prisme pentagonal droit, Alors que si les bords sont inclinés dans les bases, alors c'est un prisme pentagonal oblique. Dans l'image suivante, il y a un exemple de chacun.

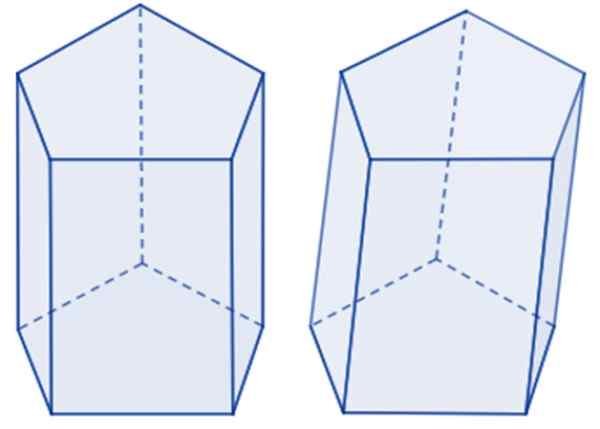Prisme pentagonal à gauche et oblique à droite. Source: Wikimedia Commons.

Le pentagone de base peut être régulier si ses cinq côtés ont la même mesure, ainsi que des angles internes, sinon c'est un pentagone irrégulier. Si la base de prisme est régulière, il s'agit de prisme pentagonal régulier. Sinon est un prisme Pentagone irrégulier.

Prismes pentagonaux de base irréguliers utilisés dans la construction moderne. Source: Fond d'écran de papier peint.

Le prisme pentagonal est une structure harmonieuse qui est utilisée dans l'architecture et la conception d'objets, comme le bâtiment moderne illustré dans la figure supérieure. Les fenêtres en forme de Pentagone irrégulières forment la base des prismes.

[TOC]

Caractéristiques du prisme pentagonal

-Il s'agit d'une figure géométrique à trois dimensions, les surfaces qui le composent contiennent un certain volume.

-Leurs bases sont des pentagones et leurs faces latérales peuvent être des rectangles ou des parallélograts.

-Il a des sommets - les coins du prisma-et des bords -bordes ou des rives-.

-Si les bords qui unissent les bases leur sont perpendiculaires, le prisme est droit, et s'ils sont enclins, le prisme est oblique.

-Lorsque la base est un pentagone dont les angles internes sont inférieurs à 180 °, le prisme est convexe, Mais si un ou plusieurs angles internes sont supérieurs à 180 °, c'est un prisme concave.

Éléments du prisme pentagonal

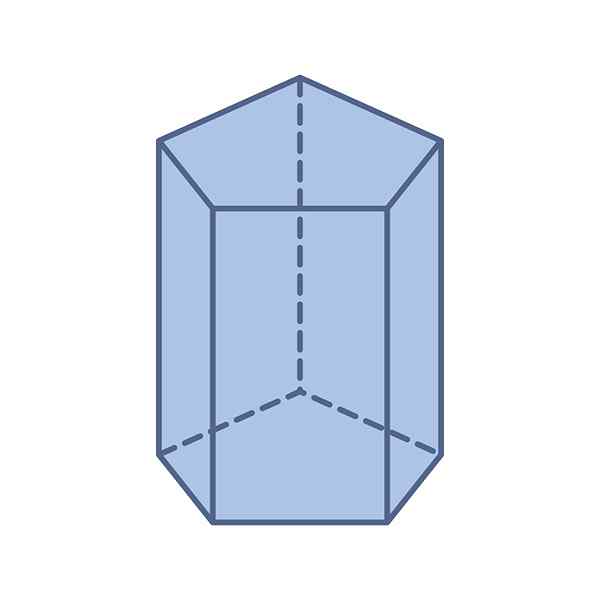
-Bases: Il a deux bases pentagonales et congruentes - leurs mesures sont les mêmes - les mêmes ou irréguliers.

Peut vous servir: formule générale: équations quadratiques, exemples, exercices

-Visages: Un prisme pentagonal a un total de 7 visages: les deux bases pentagonales et les cinq parallélogrammes qui composent les côtés.

-Bord: segment qui rejoint deux bases, illustrée en rouge sur la figure 3 ou celle qui rejoint les deux côtés.

-Hauteur: Distance entre les visages. Si le prisme est droit, cette distance coïncide avec la taille du bord.

-Sommet: point commun entre une base et deux côtés latéraux.

La figure inférieure montre un prisme pentagonal de base régulier, dans lequel les segments qui forment la base ont une mesure égale, appelée pour.

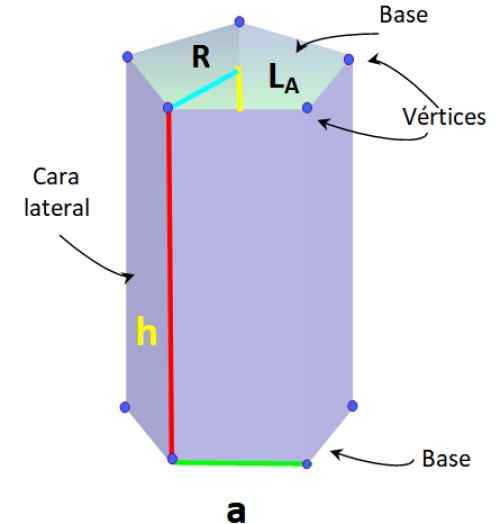 Éléments de prisme pentagonal réguliers. Source: F. Zapata.

Ce type de prisme a également les éléments suivants, typiques du Pentagone ordinaire:

-Radio R: Distance entre le centre du Pentagone et l'un des sommets.

-Apothem L_POUR: segment qui rejoint le centre avec le point médian de l'un des côtés du Pentagone.

Combien de sommets a un prisme pentagonal?

Dans un Pentagone, il y a 5 sommets et comme le prisme pentagonal a deux pentagones comme bases, ce corps a un total de 10 sommets.

Combien d'arêtes a un prisme pentagonal?

Vous pouvez calculer le nombre de bords pour les corps géométriques avec des faces plates, telles que les prismes, en utilisant le Théorème d'Euler Pour les polyèdros convexes. Leonhard Euler (1707-1783) est l'un des plus grands mathématiciens et physiques de l'histoire.

Le théorème établit une relation entre le nombre de visages, que nous appellerons C, la quantité de sommets V et les bords totaux A comme suit:

C + V = A + 2

Pour le prisme pentagonal que nous avons: c = 7 et v = 10. Effacement à, le nombre d'arêtes:

Il peut vous servir: fonction de bijjectif: qu'est-ce que c'est, comment se fait-il, des exemples, des exercices

A = c + v-2

Remplacement des valeurs:

A = 7 + 10 - 2 = 15

Un prisme pentagonal a 15 arêtes.

Comment obtenir le volume d'un prisme pentagonal?

Le volume du prisme pentagonal mesure l'espace verrouillé par les côtés et les bases. Il s'agit d'un montant positif calculé par la propriété suivante:

Tout plan qui se coupe en prisme perpendiculairement à ses bords, génère une intersection de la même manière que la base, c'est-à-dire un pentagone des mêmes dimensions.

Par conséquent, le volume du prisme pentagonal est le produit de la zone de base et la hauteur du prisme.

Être POUR_B la zone de base pentagonale et H La hauteur du prisme, puis le volume V est:

V = a_B x h

Cette formule est générale, valide pour tout prisme, régulier ou irrégulier, droit ou oblique.

Le volume d'un prisme se présente toujours en unités de longueur haut dans le cube. Si la longueur des côtés et la hauteur du prisme sont données en mètres, le volume est exprimé en m³, Ce "mètres cubes" est lu. Les autres unités incluent CM³, km³, pouces³ et de plus.

- Volume de prisme pentagonal régulier

Dans le prisme pentagonal régulier, les bases sont des pentagons réguliers, ce qui signifie que les angles latéraux et internes sont les mêmes. Compte tenu de la symétrie du corps, de la zone du pentagone et donc le volume est facilement calculé de plusieurs manières:

Connaître la hauteur et la mesure du côté

Être pour La mesure du côté de la base pentagonale. Dans ce cas, la zone est calculée par:

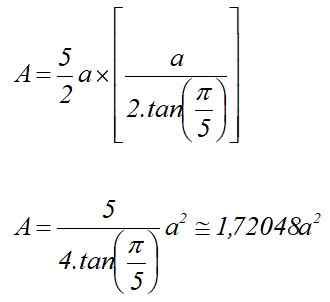
Par conséquent, le volume du prisme pentagonal régulier de la hauteur H est:

Peut vous servir: Nombres imaginaires: propriétés, applications, exemples

V = 1.72048 A²⋅ H

Connaître la hauteur et la mesure de la radio

Quand le Radio R De la base pentagonale, cette autre équation peut être utilisée pour la zone de base:

A = (5/2) R²⋅ Sen 72º

De cette façon, le volume du prisme pentagonal est donné par:

V = (5/2) R² ⋅ H ⋅ Sen 72º

Où H C'est la hauteur du prisme

Connaître la hauteur, la mesure de l'apothéme et de la valeur du périmètre

La zone de base pentagonale peut être calculée si son périmètre P est connu, qui est simplement la somme des côtés, ainsi que la mesure de l'apothème l l_POUR:

A = p. L_POUR / 2

Multiplier cette expression par la valeur de la hauteur H, Nous avons le volume du prisme:

V = P. L_POUR .H / 2

- Volume de prisme pentagonal irrégulier

La formule donnée au début est même valable lorsque la base du prisme est un pentagone irrégulier:

V = a_B x h

Pour calculer la zone de base, diverses méthodes sont utilisées, par exemple:

-Méthode de triangulation, qui consiste à diviser le Pentagone en triangles et quadrilatéraux, dont les zones respectives sont facilement calculées. La zone du Pentagone sera la somme des zones de ces chiffres plus simples.

-Méthode des déterminants de Gauss, pour lesquels vous devez connaître les sommets de la figure.

Une fois la valeur de la zone déterminée, elle est multipliée par la hauteur du prisme pour obtenir le volume.

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Référence ouverte en mathématiques. Zone de polygone. Récupéré de: MathpenRef.com.
3. Formules d'univers. Théorème d'Euler pour les polyèdros. Récupéré de: universoformules.com.
4. Formules d'univers. Zone d'un pentagone ordinaire. Récupéré de: universoformules.com.
5. Wikipédia. Prisme. Récupéré de: est.Wikipédia.com.
6. Wikipédia. Prisme pentagonal. Récupéré de: est.Wikipédia.com.