Prisme hexagonal

Nous expliquons ce qu'est un prisme hexagonal, ses caractéristiques, ses éléments, la zone, les sommets, les bords et comment les calculer.

Qu'est-ce qu'un prisme hexagonal?

UN Prisme hexagonal Il s'agit d'un corps à trois dimensions composé de deux formes hexagonales et des côtés en forme de rectangle ou de parallélogramme. Il peut être trouvé dans la nature, dans la structure cristalline des minéraux tels que le béryllium, le graphite, le zinc et le lithium, par exemple.

Les éléments d'un prisme hexagonal sont la base, le visage, le bord, la hauteur, le sommet, la radio et l'apothème. De eux, vous pouvez calculer les zones et les volumes.

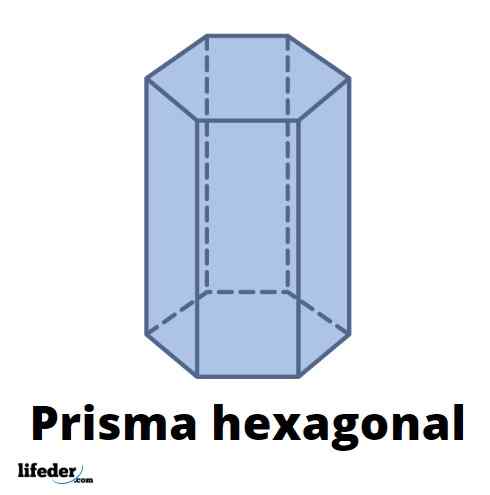
La figure supérieure montre un prisme hexagonal avec des visages latéraux rectangulaires; c'est-à-dire, Un prisme hexagonal droit. Les hexagones des bases sont réguliers, c'est-à-dire que leurs côtés internes et leurs angles sont les mêmes. Cependant, les visages du prisme hexagonal peuvent être des hexagones irréguliers.

Caractéristiques du prisme hexagonal

1- Le prisme hexagonal est une figure tridimensionnelle avec des bases hexagonales.

2- Il existe une grande variété d'objets qui répondent à cette définition et pourtant ils sont très différents.

Dans la figure suivante, il existe une variété de prismes hexagonaux: à gauche, un prisme hexagonal droit de visages réguliers, à droite et en bas de deux prismes hexagonaux de visages irréguliers. L'hexagone à la base du prisme ci-dessous a une particularité: c'est concave, Ce qui signifie que certains de ses angles internes sont supérieurs à 180 °.

Variété de prismes hexagonaux. Source: Wikimedia Commons.

D'un autre côté, les bases hexagonales des prismes ci-dessus sont des polygones convexe: Tous les angles internes mesurent moins de 180 °.

Éléments de prisme hexagonal

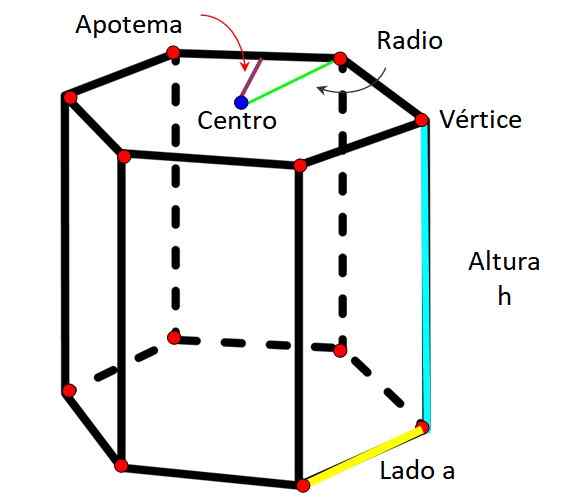Éléments de prisme hexagonal. Source: F. Zapata

Comme chaque prisme, le prisme hexagonal est caractérisé par les éléments suivants:

Peut vous servir: inverse multiplicatif: explication, exemples, exercices résolus

-Bases: en nombre de deux (2), sous la forme d'hexagone et de congruente, c'est-à-dire une égale mesure. Les visages hexagonaux peuvent être réguliers ou irréguliers.

-Visages: Un prisme hexagonal a huit (8) visages au total, qui peuvent être comptés en utilisant la figure 1. Sur les 8 faces, deux (2) sont des bases et six (6) sont latérales.

-Bord: C'est le segment qui rejoint deux bases ou deux côtés du prisme.

-Hauteur: C'est la distance entre les deux faces du prisme. Coïncide avec la longueur du bord dans le cas du prisme droit.

-Sommet: point commun entre une base et deux côtés latéraux.

Si les bases du prisme sont régulières, la symétrie de la figure permet de définir des éléments supplémentaires du côté hexagone ordinaire pour.

-Radio: C'est la distance mesurée du centre de l'hexagone et de tout sommet.

-Apothème: C'est le segment qui va du centre du visage hexagonal au milieu d'un côté.

Avec l'aide de ces éléments, les zones et les volumes sont calculés, comme nous le verrons plus tard.

Formules

Il existe de nombreuses formules liées au prisme hexagonal. Ils servent à calculer la zone de leurs bases et visages latéraux, son volume et d'autres caractéristiques importantes. Les zones de l'hexagone ordinaire, de l'hexagone irrégulière et du parallélogramme, ainsi que les périmètres, sont utiles.

Périmètre d'une figure plate

C'est la mesure de son contour, qui dans le cas d'un polygone comme l'hexagone est la somme de ses côtés. Si l'hexagone est régulier pour, Il y a une formule pour le périmètre P:

P = 6.pour

Zone hexagone ordinaire

Appelons ALS et L_POUR Sur la longueur de l'apothème. La zone est donnée par:

Peut vous servir: données non groupées: exemples et exercice résolus

A = p. L_POUR/ 2 = 6a. L_POUR/ 2

Où P est le périmètre de la figure.

En fonction de la taille du côté pour, La zone peut également être calculée par:

A = 2.5981.pour²

Zone hexagone irrégulière

Il n'y a pas de formule spécifique, car elle dépend de la disposition des côtés, mais l'hexagone peut être divisé en triangles, calculer la zone de chacun et les ajouter.

Une autre méthode pour trouver la zone est celle des déterminants de Gauss, pour lesquels il est nécessaire de connaître les coordonnées des sommets hexagonaux.

Zone de parallélogramme

A = hauteur de base x

Ouais pour est la base et H C'est la hauteur, la zone est:

A = a.H

Zone de prisme hexagonal

C'est la somme des zones des bases - deux hexagones - et ceux des faces -6 rectangles ou parallélogrammes-.

Zone de prisme hexagonal ordinaire

Si le prisme hexagonal a les bases sous la forme d'hexagones ordinaires et que les bords latéraux sont perpendiculaires à ces bases, sa zone est donnée par la somme:

A = 2 x 2.5981.pour² + 6e.H

Où pour C'est le côté de l'hexagone et H C'est la hauteur du prisme.

Zone de prisme hexagonal irrégulier et droit

Si les bases sont des hexagones irréguliers, la zone est calculée par:

A = 2a_base  + P.H

Où:

-POUR_base C'est la zone de base hexagonale irrégulière.

-P est le périmètre de la base.

-H est la hauteur du prisme

Sommets

Chaque visage hexagonal a 6 coins ou sommets, ce qui donne un total de 12 sommets pour le prisme hexagonal.

Bords

Il existe une formule pour trouver le nombre de bords d'un prisme. Il a été découvert par le grand mathématicien Leonhard Euler (1707-1783) et est appelé Théorème d'Euler pour les polyèdros. Dit ainsi:

Peut vous servir: raisonnement algébrique

Si C est le nombre de visages, et la quantité de Vértices V et les bords totaux. C'est vrai que:

C + V = A + 2

Les montants du prisme hexagonal sont: C = 8 et V = 12. Par conséquent, A est:

A = c + v - 2 = 8 + 12-2 = 18

Volume

Le volume V de tout prisme, qu'il soit droit ou oblique, de visages réguliers ou irréguliers, est donné par:

V = zone de base x hauteur

Par conséquent, nous aurons besoin des formules de la zone que nous avons vue précédemment.

Par exemple, pour un prisme hexagonal droit, dont les bases sont des hexagones réguliers, le volume est donné par:

V = 2.5981.pour².H

Les références

1. Référence ouverte en mathématiques. Zone de polygone. Récupéré de: MathpenRef.com.
2. Wikipédia. Prisme. Récupéré de: est.Wikipédia.com.