Plan cartésien

Quel est l'avion cartésien?

Il plan cartésien Il se compose d'une paire de lignes droites perpendiculaires les unes aux autres et qui se croisent à un moment donné. L'une des lignes est verticale et l'autre horizontale, en mettant au point d'intersection comme l'origine du système.

L'objectif est de localiser facilement n'importe quel point plat à travers une paire de valeurs: coordonnées. Pour ce faire, sur chacune des lignes, une échelle avec des nombres entiers est construite, les positives sont écrites dans une direction et les négatifs de l'autre, comme le montre la figure suivante:

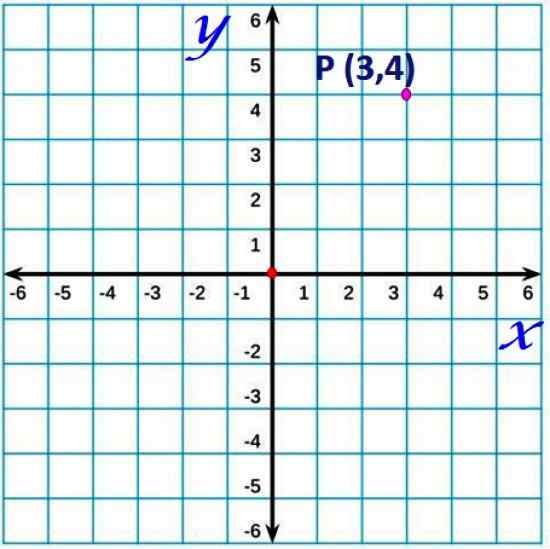
Figure 1. Un point dans l'avion cartésien. Source: F. Zapata.

Par convention, l'axe horizontal est généralement appelé x et axe vertical comme axe et.

Un point de l'avion aura des coordonnées spécifiées par une paire ordonnée (X, y). Par exemple, le point P des coordonnées (3,4), situé à 3 unités à droite de l'origine et 4 unités vers le haut, dans la figure supérieure. Il est similaire à une carte, ce qui indique la latitude et la longueur d'un certain emplacement.

Comme deux coordonnées sont nécessaires, il est dit que l'avion est à deux dimensions, mais le concept est facilement étendu à trois dimensions, ajoutant un axe plus coordonné, qui est généralement indiqué comme l'axe z. Dans ce cas, les coordonnées prennent forme (X y Z).

L'avion cartésien reçoit son nom du scientifique français René Descartes (1596-1650), qui l'a formalisé dans son travail Discours de méthode de 1637, bien qu'il y ait une histoire dans les œuvres d'Apollonius de Perga (262-190 AC), le mathématicien qui a découvert les courbes coniques: circonférence, ellipse, parabole et hyperbole.

Peut vous servir: différence de cubes: formules, équations, exemples, exercices

Caractéristiques de l'avion cartésien

- Comme il Axe x comme lui Axe y Ils s'étendent infiniment aux deux extrémités et se croisent perpendiculairement (à un angle de 90 degrés). Cette fonction est appelée orthogonalité.

- Le point où les deux axes se croisent est connu sous le nom d'origine ou de point zéro.

- Le système de coordonnées divise l'avion en quatre régions appelées quadrants.

- Les emplacements du plan de coordonnées sont décrits comme des paires ordonnées.

- Chaque point sur le plan cartésien est associé à une coordonnée X unique et à une coordonnée et unique.

Éléments de l'avion cartésien

Les éléments du plan cartésien sont les suivants:

-Le lignes numériques soit coordonnées x et y, Si c'est l'avion. L'axe et recevoir le nom de l'axe des ordonnées, tandis que l'axe X C'est l'axe de l'abscisse. En ce qui concerne l'espace, l'axe est ajouté z, capable de représenter à la fois la hauteur et la profondeur.

-Il Origine, qui est le point d'intersection des axes.

-Les quadrants, Quelles sont les régions que les axes de coordonnées déterminent sur le plan et sont comptés dans la direction opposée aux mains de l'horloge, en commençant par le premier quadrant. Ils sont définis comme suit:

• Premier quadrant: axes X et et positif.
• Deuxième quadrant: correspondant à l'axe x négatif et à l'axe et positif.
• Troisième quadrant: il a les deux axes négatifs.
• Quatrième quadrant: avec l'axe x positif et l'axe et négatif.

Généralement, les quadrants sont désignés en nombre romain, comme ceci:

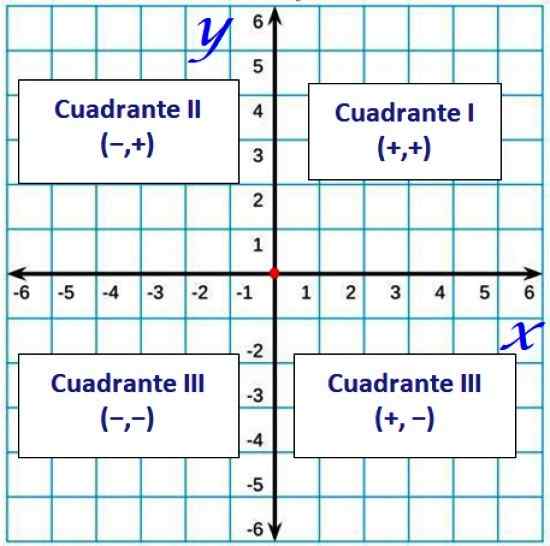Figure 2. Cuadrants dans le plan cartésien. Source: F. Zapata.

Paies et distance commandées entre deux points

Les paires ordonnées sont les coordonnées de chaque point, dans lesquelles la coordonnée x est toujours placée en premier, comme dans l'exemple de la figure 1. Les coordonnées (3,4) du point P indiquent que x = 3 et y = 4.

Dans cette autre figure ci-dessous, le point P appartient au quadrant IV et a des coordonnées (2; −1.5). Notez qu'en projetant des lignes des axes de coordonnées au point P formes un rectangle. C'est la raison pour laquelle les coordonnées cartésiennes sont également appelées Coordonnées rectangulaires.

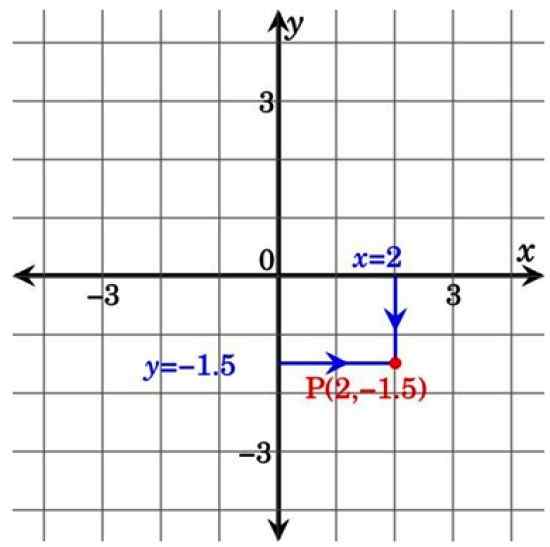figure 3. Point sur l'avion cartésien. Source: Wikimedia Commons.

Applications d'avion cartésiennes

L'avion cartésien a de nombreuses applications dans de nombreux domaines. Initialement, Descartes l'a introduit pour graphiquement les courbes de courbes dans le plan, c'est pourquoi elle est considérée comme le père de la géométrie analytique.

Peut vous servir: produit Cruz

Cependant, son utilisation s'étend pour représenter toutes sortes de relations et de fonctions, telles que:

-Suivez la trajectoire d'un corps avec un mouvement parabolique, circulaire ou curviligne en général.

-Déterminez graphiquement la façon dont deux variables sont liées via une fonction.

-Localisez des points sur des terrains plats pour faciliter les mesures.

Les références

1. Les mathématiques sont amusantes. Coordonnées cartésiennes. Récupéré de: Mathsisfun.com / data / coordonnées cartésiennes.
2. L'avion cartésien. Récupéré de: DL.UNCW.Édu.