Paire ordonnée

Qu'est-ce qu'une paire ordonnée?

Une paire ordonnée ou duo Il s'agit d'un ensemble de deux éléments qui sont écrits selon l'ordre établi par un certain critère. Dit critères spécifie lequel des deux éléments va en premier et lequel va après.

La paire ordonnée est indiquée (x, y), où "x" est le premier élément de la paire et "y" est le second, également appelé Composants. En général (x, y) ce n'est pas le même couple bien rangé (y, x). Et en plus de l'ordre, une autre caractéristique importante des paires ordonnées est l'égalité: deux paires ordonnées (a, b) et (c, d) ne sont les mêmes que si a = c et b = d.

Figure 1.- Grâce aux paires bien rangées, le chiot sait que les os sont enterrés dans les endroits (3,1) et (-4,2), tandis que sa maison est dans (0,0). Source: F. Zapata.

Des exemples de paires ordonnées seraient celles qui sont composées de l'âge et le poids d'un cours d'étudiants en mathématiques. La paire ordonnée (15, 62) correspond à un étudiant de 15 ans, différent de la paire improbable (62,15).

Le concept de couple ordonné est très important dans divers domaines de mathématiques, comme le plan cartésien, les fractions, les vecteurs dans le plan, les relations et les fonctions. Un aspect important est que leurs éléments n'ont pas nécessairement de numérique, par exemple, ils peuvent être commandés avec:

• Ville du pays
• Prénom Nom de famille
• Épouse époux

Et de nombreuses autres combinaisons.

Exemples de paires ordonnées

Fractions

Une fraction est représentée comme le quotient de deux entiers P / Q, par exemple la fraction ½, ce qui équivaut au numéro décimal 0.5.

Cependant, cette fraction n'est pas la seule qui représente la décimale 0.5, il en va de même pour les éléments suivants:

2/4; 3/6; (-2) / (- 4); 20/40; (-1) / (- 2)…

De cette façon, toute fraction peut être représentée comme une paire ordonnée (P, Q), où P et Q sont entiers, P occupant la position du numérateur et Q celle du dénominateur. Il y a une restriction importante et que Q (le dénominateur) doit être différent de 0, car les fractions de la forme P / 0 ne sont pas définies.

Peut vous servir: ensemble fini: propriétés, exemples, exercices résolus

Et une autre condition importante est que deux fractions A / B et C / D sont égales tant qu'elle est remplie que:

A ∙ d = b ∙ c

Fonctions et ses graphiques

Une fonction peut être exprimée comme un ensemble de paires bien rangées. Par exemple, en représentant graphiquement une fonction dans le plan cartésien, le premier élément se voit attribuer la position de la variable indépendante, tandis que le second se voit attribuer la variable dépendante. Ceci est une paire ordonnée.

Pour la fonction y = f (x), le couple rangé peut être exprimé comme [x, f (x)]]. Par exemple, considérez l'ensemble de départ:

A = 1, 2, 3, 4

Dans cet ensemble, il y a les premiers composants d'une paire ordonnée selon la fonction y = x². L'ensemble des deuxième composants est:

B = 1, 4, 9, 16

Et les paires ordonnées sont formées sont:

(1,1); (2,4); (3, 9); (4; 16)

Égard.

Vecteurs dans l'avion

Les vecteurs peuvent être représentés dans le plan cartésien par des paires ordonnées, où le premier élément représente le composant horizontal "x" et le second le composant vertical "Y". Pour distinguer les vecteurs des points de l'avion, ils sont désignés par des lettres audacieuses et les crochets sont utilisés à la place des parenthèses, comme ceci:

V =

Par exemple, le vecteur V = a une composante horizontale égale à 4 et une composante verticale égale à 7. Son graphique est:

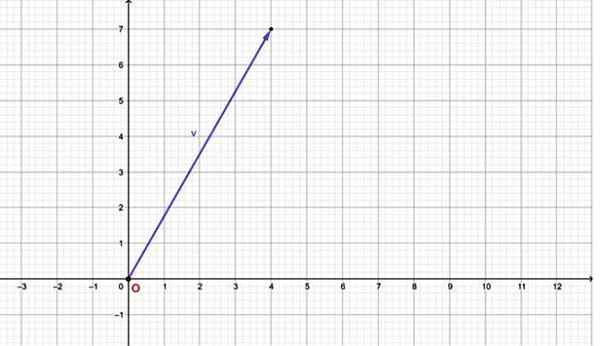Figure 2.- Un vecteur d'avion peut être exprimé par une paire ordonnée. Source: F. Zapata.

Notez que ce vecteur a son origine coïncidant avec l'origine du système de coordonnées (0,0). Si le vecteur a son origine à un autre point, il peut également être exprimé sous la forme d'un couple ordonné à travers une paire ordonnée, pour le faire, voir les sections suivantes.

Peut vous servir: hiérarchie des opérations

Opérations Pares ordonnées

Ajout

Soit les cibles (a, b) et (c, d) paires (d). Un nouveau couple est obtenu au moyen de sa somme selon:

(a, b) + (c, d) = (a + c, b + d)

Élément neutre

L'élément neutre de l'ajout de paires ordonnées est le couple (0,0), car lorsqu'il ajoute à la paire ordonnée (A, B), la somme est ce dernier:

(a, b) + (0,0) = (a, b)

Somme du contraire

En ajoutant une paire ordonnée (a, b) avec son opposé (-a, -b), le couple ordonné (0,0) est obtenu:

(a, b) + (-a, -b) = (0,0)

Commutativité

L'ordre des ajouts ne modifie pas la somme:

(a, b) + (c, d) = (c, d) + (a, b)

Association

Le résultat de l'ajout de trois paires ordonnées n'est pas modifiée lorsqu'il est regroupé pour effectuer l'opération:

[(a, b) + (c, d)] + (e, f) = (a, b) + [(c, d) + (e, f)]

Soustraction des paires ordonnées

Que les cibles (a, b) et (c, d) soient, la soustraction est effectuée comme suit:

(a, b) - (c, d) = (a-c, b-d)

Produit

Dans le produit, il existe deux options: i) Multipliez un couple commandé par une constante et ii) multiplier deux (ou plus) plans.

Multiplication par une constante

Soit K une constante et le couple ordonné (A, B), le produit entre la constante et le couple est:

K ∙ (a, b) = (k ∙ a, k ∙ b)

Multiplication des paires ordonnées

Le produit entre les paires commandées (a, b) et (c, d) est réalisée comme suit:

(a, b) x (c, d) = (ac - bd, bc + ad)

Élément neutre

L'élément neutre de la multiplication est (1.0), car en multipliant tout couple ordonné par cela, suivant la règle de multiplication décrite ci-dessus, le couple d'origine est:

(a, b) x (1.0) = (a - 0, b + 0) = (a, b)

Peut vous servir: inverse multiplicatif: explication, exemples, exercices résolus

Association

Comme l'ordre des facteurs ne modifie pas le produit, il peut être regroupé de différentes manières pour multiplier trois paires bien rangées et le résultat est le même:

[(a, b) x (c, d)] x (e, f) = (a, b) x [(c, d) x (e, f)]

Exercices résolus

Exercice 1

Vous avez commandé des paires (x², X-2) = (16, 2). Qui est la valeur de x?

Solution

L'application de l'égalité des paires ordonnées est obtenue en premier:

X² = 16 ⇒ x₁ = 4, x₂ = -4

Pour savoir lequel des deux valeurs choisit, l'utilisation de:

X-2 = 2

x = 2 + 2 = 4

Par conséquent, la valeur demandée de x est 4.

Exercice 2

Exprimez comme une paire ordonnée le vecteur qui passe du point (1, 3) au point (7, 11) et le représente graphiquement.

Solution

Être V Le vecteur fouillé. Pour déterminer la paire ordonnée qui le représente et qui contient ses coordonnées, les coordonnées du point d'arrivée et le point d'origine sont soustraites, dans cet ordre. Donc:

V = =

Le vecteur est alors représenté V comme celui qui passe de (1.3) à (7, 11) et l'équipement V dont l'origine est fixée à l'origine du système de coordonnées (0,0). Comme vous pouvez le voir, ils ont la même direction et le même sens.

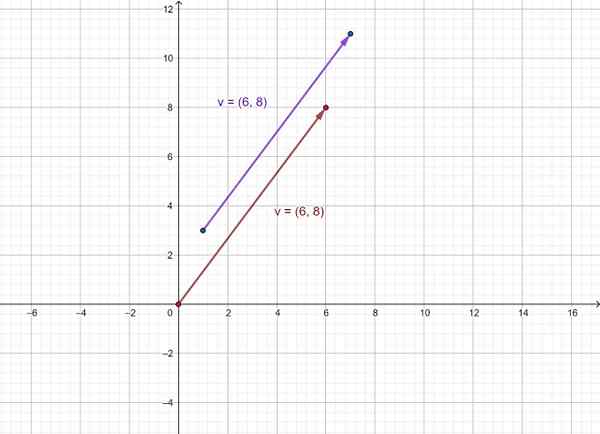figure 3. Représentation d'un vecteur comme paire ordonnée. Source: F. Zapata.

Les références

1. Profond. Paire ordonnée. Récupéré de: Deepai.org.
2. Mathémovil. Représentation cartésienne d'un vecteur par une paire ordonnée. Récupéré de: Matemovil.com.
3. Varsity Tutorrs. Paire ordonnée. Récupéré de: WarsityTorm.com
4. Priestri, Juan. Relations et fonctions. Faculté d'ingénierie. Département des mathématiques. Université de Buenos Aires. Récupéré de: Sujets.Fi.Uba.ardente.
5. Université de Denver. Rapports. Récupéré de: mathématiques.Ucdenver.Édu.