Vagues unidimensionnelles Expression mathématique et exemples

Le Vagues unidimensionnelles Ce sont eux qui se propagent dans une direction, que les vibrations se produisent ou non dans la même direction de propagation. Un bon exemple d'entre eux est la vague qui se déplace le long d'une corde tendue comme celle d'une guitare.

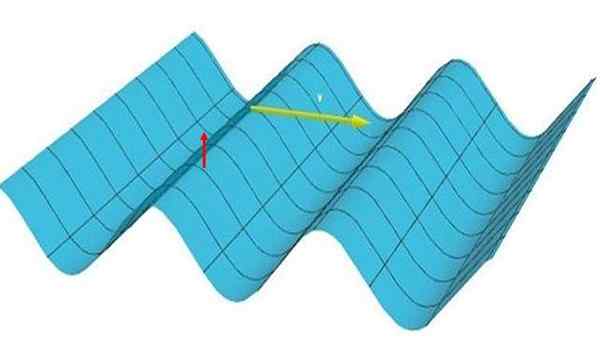
Dans une vague plate croix, Les particules vibrent verticalement (elles grimpent et descendent, voient la flèche rouge sur la figure 1), mais c'est une dimension parce que la perturbation se déplace dans une direction, après la flèche jaune.

Figure 1: L'image représente une onde unique. Notez que les crêtes et les vallées forment des lignes parallèles les unes avec les autres et perpendiculaires à la direction de propagation. Source: auto-faite.

Les vagues unidimensionnelles apparaissent assez fréquemment dans la vie quotidienne. La section suivante décrit quelques exemples d'entre eux et aussi de vagues qui ne sont pas unidimensionnelles, pour établir clairement les différences.

[TOC]

Exemples d'ondes unidimensionnelles et d'ondes non unidimensionnelles

Vagues unidimensionnelles

Ce sont quelques exemples d'ondes d'une dimension qui peuvent être facilement observées:

- Une impulsion sonore qui se déplace à travers une barre droite, car c'est une perturbation qui se propage dans la barre.

- Une vague qui se déplace à travers un canal d'eau, même lorsque le déplacement de la surface de l'eau n'est pas parallèle au canal.

- Les vagues qui se propagent sur une surface ou à travers l'espace à trois dimensions peuvent également être une seule dimension, à condition que leurs fronts d'onde soient des plans parallèles les uns aux autres et voyagent dans une direction.

Vagues non dimensionnelles

Un exemple d'une onde non dimensionnelle se trouve dans les vagues qui se forment sur une surface d'eau immobile lorsqu'une pierre est tombée. C'est une onde à deux dimensions avant de l'onde cylindrique.

Peut vous servir: bras de levierFigure 2. L'image représente un exemple de ce qui n'est pas une onde unique. Notez que les crêtes et les vallées forment des cercles et que la direction de propagation est radiale vers l'extérieur, c'est alors une onde circulaire à deux dimensions. Source: Pixabay.

Un autre exemple d'onde dimensionnelle non syndiquée est l'onde sonore qui génère un pétard par explosion à une certaine hauteur. Ceci est une onde à trois dimensions avec des fronts d'onde sphérique.

Expression mathématique d'une onde unique

La manière la plus générale d'exprimer une onde unique qui se propage sans atténuation dans le sens positif de l'axe X Et avec la vitesse V C'est mathématiquement:

et (x, t) = f (x - v.t)

Dans cette expression et représente la perturbation de la position X à l'instant t. La forme d'onde est donnée par la fonction F. Par exemple, la fonction d'onde illustrée à la figure 1 est:  et (x, t) = cos (x - v t) Et l'image de l'onde correspond au moment t = 0.

Une onde comme celle-ci, décrite par une fonction cosinus ou sinusale, est appelée vague harmonique. Bien que ce ne soit pas la seule forme d'onde qui existe, elle est de la plus haute importance, car toute autre onde peut être représentée comme un chevauchement ou une somme des ondes harmoniques. C'est la connaissance Théorème de Fourier, donc utilisé pour décrire les signaux de toutes sortes.

Lorsque l'onde se déplace dans le sens négatif de l'axe x, cela change simplement V pour -V En argument, être:

et (x, t) = g (x + v t)

La figure 3 montre l'animation d'une onde qui se déplace vers la gauche: c'est une forme appelée fonction Lorentziana et elle L'expression mathématique est:

Peut vous servir: travail: formule, unités, exemples, exercices

et (x, t) = 1 / (1 + (x + 1⋅t)²

Dans cet exemple, la vitesse de propagation est v = 1, -une unité d'espace pour chaque unité de temps-.

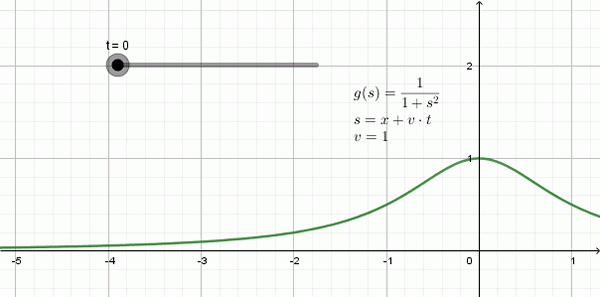figure 3. Exemple d'une onde lorentzienne qui se déplace rapidement vers la gauche v = 1. Source: Préparé par F. Zapata avec Geogebra.

Équation des ondes unidimensionnelles

L'équation des vagues est une équation en dérivés partiels, dont la solution est bien sûr une vague. Il établit la relation mathématique entre la partie spatiale et sa partie temporelle, et a la forme:

La solution, qui est précisément la fonction y (x, t), peut être vérifiée par remplacement et développement dans cette équation. Par exemple, fonctions f (x - v t)  et  G (x + vt)  mentionné, ce sont des solutions d'équation des vagues.

Exemple résolu

Ensuite, vous avez l'expression générale y (x, t) pour une onde harmonique:

et (x, t) = a⋅cos (k⋅x ± Ω⋅t + θo)

A) Décrire la signification physique des paramètres A, K, ω et θo.

b) quel sens ont les signes ± sur l'argument du coseno?

c) Vérifiez que l'expression donnée est en effet la solution de l'équation d'onde de la section précédente et trouvez la vitesse V de propagation.

Solution à)

Les caractéristiques de la vague sont dans les paramètres suivants:

-POUR représente le amplitude ou "hauteur de vague".

-k est dans Numéro d'onde Et il est lié à la longueur d'onde λ à travers K = 2π / λ.

-Ω C'est fextension angulaire Et il est lié au période T oscillation des vagues par

Ω = 2π / t.

-θo C'est le phase initiale, qui est lié au point de départ de la vague.

Peut vous servir: frottement statique: coefficient, exemple, exercice

Solution b)

Le signe négatif est pris si la vague se déplace dans le sens positif de l'axe x et le signe positif autrement.

Solution C)

Vérifiez que l'expression donnée est une solution à l'équation d'onde est simple: la dérivée partielle de la fonction est prise et (x, t) En ce qui concerne X deux fois, il est partiellement dérivé de T deux fois, puis les deux résultats se rencontrent pour obtenir l'égalité:

Deuxième dérivé de x: ∂²et / ∂x²= -K². POUR⋅cos (k⋅x ± Ω⋅t + θo)

Deuxième dérivé de t: ∂²et / ∂t²= -Ω². POUR⋅cos (k⋅x ± Ω⋅t + θo)

Ces résultats sont remplacés dans l'équation des vagues:

 -k². POUR⋅cos (k⋅x ± Ω⋅t + θo) = (1 / v²) (-Ω². POUR⋅cos (k⋅x ± Ω⋅t + θo))

Tellement POUR Comme le cosinus est simplifié, car ils apparaissent des deux côtés de l'égalité et l'argument du cosinus est le même, donc l'expression est réduite à:

-k² = (1 / V²) (-Ω²)

Qui permet d'obtenir une équation pour V en termes de Ω et k:

V² = Ω² / k²

v = ± Ω / k

Les références

1. E-éducatif. Équation des ondes harmoniques unidimensionnelles. Récupéré de: e-decative.Cathedu.est
2. Le Rincón de la physique. Classes de vagues. Récupéré de: Physique.Blogspot.com.
3. Figueroa, D. 2006. Vagues et physique quantique. Série: Physique pour la science et l'ingénierie. Édité par Douglas Figueroa. Université Simon Bolivar. Caracas, Venezuela.
4. Laboratoire de physique. Le mouvement des vagues. Récupéré de: Fisicalab.com.
5. Peirce, un. Conférence 21: L'équation des ondes unidimensionnelles: la solution d'Alembert. Récupéré de: UBC.CA.
6. Équation des vagues. Récupéré de: dans.Wikipédia.com