Concept, types et exemples d'ondes de dimension

Ils sont ondes à trois dimensions Ceux qui se propagent dans l'espace, par exemple l'onde sonore produite par un haut-parleur. Cette vague se propage dans toutes les directions, mais pas avec la même intensité dans chacun d'eux.

Si une perturbation se produit à un point dans l'espace, elle se propage dans les trois directions spatiales, les fronts d'onde avant étant fermés, sphériques, elliptiques ou un autre type.

Ondes à trois dimensions produites par un haut-parleur

D'un autre côté, si l'endroit d'où proviennent les vagues, c'est-à-dire que la source a une distribution plate, alors la perturbation se déplacera principalement dans la direction perpendiculaire à ce plan, formant des fronts d'onde plats.

[TOC]

Types de vagues à trois dimensions

Dans les vagues de trois dimensions, les fronts d'onde sont un ensemble de surfaces immergées dans un espace à trois dimensions.

Maintenant, le front des vagues est le lieu géométrique des points d'espace qui sont obtenus par la perturbation initiale, au même moment du temps.

Trois types d'ondes qui se déplacent dans l'espace à trois dimensions sont généralement considérés, selon la symétrie de l'avant de l'onde: vagues plates, vagues cylindriques et ondes sphériques. Cependant, les ondes réelles n'appartiennent pas toujours à ces types, car elles n'ont pas un degré de symétrie aussi élevé.

Vagues plates

Une onde plate qui se déplace dans la direction positive du X rapidement V, est fonctionnellement représentée comme:

G (x, t) = f (x - v⋅t)

Cette vague ne se limite pas à l'axe X, mais s'étend également dans les adresses et et z. Mais la forme fonctionnelle indique que tous les points qui ont la même coordonnée x, quelles que soient les coordonnées (z, y), ont la même valeur G.

Dans ce cas, les fronts d'onde sont des plans parallèles au z-and-plan qui avance rapidement V, ce qui signifie que la vague plate occupe les trois espaces dimensionnels.

L'expression qui représente une onde plate qui se propage dans n'importe quelle direction ou rapidement V, où ou représente une unité directeurs vectoriels seniors cos (α), cos (β) et cos (γ), est:

Peut vous servir: réaction enthalpie: définition, thermochimie, exercices

g = f (û • r - v⋅t) = f (x cos (α) + et cos (β) + z cos (γ) - v⋅t)

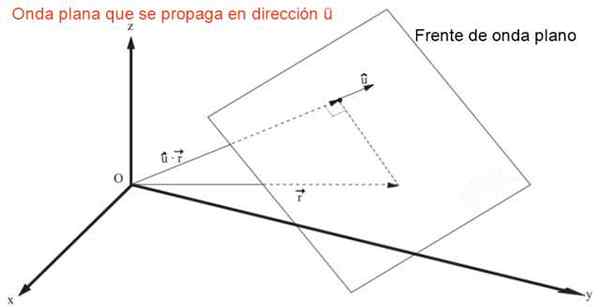Front d'onde plat qui se propage dans l'espace à trois dimensions rapidement V. Source: F. Zapata.

Il est facile de démontrer, par substitution directe, que l'expression précédente est une solution de l'équation des ondes à trois dimensions, une équation en dérivés partiels du deuxième ordre linéaire:

∂_XxG + ∂_OuiG + ∂_ZzG = (1 / v²) ∂_Ttg

L'équation précédente peut être écrite de manière plus compacte en utilisant l'opérateur Laplacien ∇²:

∇²G = (1 / v²) ∂_Ttg

Vagues cylindriques

Lorsque la perturbation initiale est distribuée sur une ligne droite, la vague se propage dans la direction radiale perpendiculaire à cette ligne remplissant l'espace à trois dimensions qui l'entoure, avec des fronts d'onde cylindriques.

Ondes sphériques

Lorsque la source est ponctuelle et que le milieu dans lequel l'onde à trois dimensions est propagée est homogène et isotrope (ses propriétés ne changent pas en fonction de la direction), alors les fronts d'onde sont des sphères concentriques au point où la perturbation initiale s'est produite.

Dans le cas d'une onde sphérique dans laquelle l'intensité de l'onde est identique dans toutes les directions, la fonction qui décrit la perturbation ne dépend que de la distance r à la source de temps et de temps t.

Dans ce cas, le laplacien correspondant est:

∇²G = (1 / r²) ∂_r(r² ∂_rg)

Être l'équation des vagues:

∇²G = (1 / v²) ∂_Ttg

La solution générale serait:

g (r, t) = (1 / r) f (r - v⋅t) + (1 / r) g (r + v⋅t)

Dans ce cas, il est dit que c'est un vague sphérique. Mais il peut y avoir des variantes, comme on le verra ci-dessous

Ondes sphériques non isotropes

Il peut également arriver qu'une onde sphérique, c'est-à-dire, avec les fronts d'onde formés par des sphères concentriques à un point central, l'amplitude ou l'intensité de l'onde est différente dans les différentes directions.

C'est ce qui se passe lorsque la source centrale de l'onde est plus efficace dans une direction que d'autres. 

Il peut vous servir: physique avant les Grecs (Grèce Antigua)

Par exemple, le son produit par une corne n'a pas la même intensité partout, même dans le cas des points équivalents du klaxon.

L'intensité n'est pas la même bien que le signal prenne le même temps pour atteindre ces points. C'est une onde sphérique qui a un motif directionnel non sphérique. 

Il y a aussi des ondes sphériques dans le cas des ondes électromagnétiques créées par une antenne, mais elles peuvent ne pas être également intenses dans toutes les directions.

Antenne de l'émetteur

La moitié non homogène

Lorsque le milieu n'est pas homogène, la vitesse de propagation de l'onde est différente dans différentes directions.

Un exemple de milieu non homogène est l'atmosphère dans laquelle il y a des différences de pression avec la hauteur et il y a des gradients de température. Un autre exemple est les strates de la croûte terrestre, qui diffèrent en densité et en module élastique. 

Les résultats de la non-homogénéité dans les fronts d'onde originaires d'une source ponctuelle centrale ne sont pas des sphères concentriques, car la distance parcourue par la vague, dans la même période, est différente dans chaque direction.

Ensuite, il y a une onde à trois dimensions dont le front de l'onde n'est pas sphérique.

Intensité et énergie d'une onde sphérique

Nous pouvons écrire l'expression d'une vague harmonique sphérique comme ceci:

g (r, t) = (g_soit / r) cos (k⋅r - ω⋅t)

Où les fronts d'onde se propagent rapidement à:

V = ω / k

Et son amplitude diminue avec l'inverse de la distance r de la source ponctuelle d'ondes sphériques.

Les ondes harmoniques ont densité d'énergie (Énergie par unité de volume) ε donné par:

ε = ½ ρ Ω² (g_soit / r)²

Dans cette équation:

-ρ Il a des unités de masse par unité de volume et représente la densité du milieu où une onde sonore se propage.

-g_soit C'est l'amplitude du déplacement d'un élément du milieu, par exemple un fluide, en raison de l'onde de propagation.

Peut vous servir: frottement visqueux (force): coefficient et exemples

Il convient de noter que, comme il s'agit d'une onde sphérique, la densité d'énergie diminue avec l'inverse du carré de la distance.

L'intensité de l'onde, c'est-à-dire l'énergie transmise par unité de temps est:

I = v⋅ε

Comme toujours, dans la pratique, l'ampleur la plus importante est la puissance transmise par zone unitaire à la distance radiale r:

P = V⋅ε = I_soit / r²

Être Toi_soit = ½ ρ V ω² g_soit².

L'énergie totale transmise par unité de temps à travers un rayon R est:  P⋅4πr²= 4π⋅i_soit, Et comme prévu, il ne dépend pas de la distance radiale. 

Exemples de vagues de trois dimensions

Les vagues à trois dimensions sont très fréquentes, nous avons donc:

Antennes d'émetteur d'ondes électromagnétiques

Les vagues produites par une antenne ou le son produit par une touche sont des vagues à trois dimensions bien que de nature différente

Ils couvrent un spectre très large, des ondes radio entre les centaines de KHz et des centaines de MHz, aux vagues émises par l'antenne de l'antenne Wifi de l'ordre des GHz, qui tombent déjà dans la gamme des micro-ondes. 

Nous savons que le micro-ondes, bien qu'ils ne soient pas un rayonnement ionisant, ils sont capables d'augmenter la température de l'organisme car il contient beaucoup d'eau.

Par conséquent, il n'est pas conseillé d'avoir l'antenne Wi-Fi près de la tête ou du corps. S'enfuir un peu, car à double distance, l'intensité est un quart.

Ondes sismiques

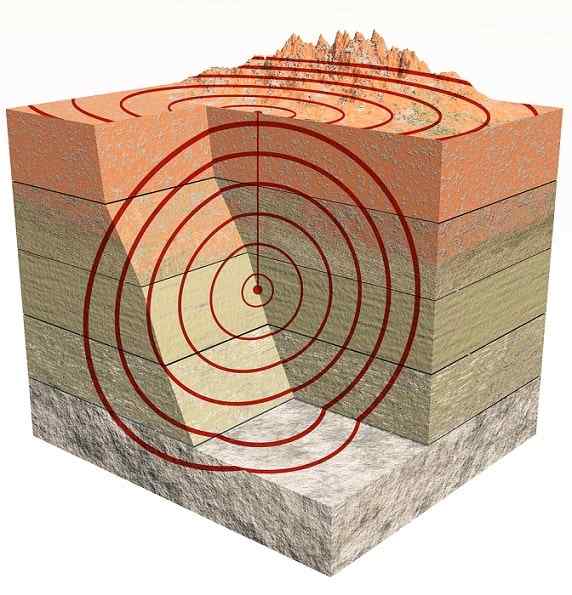Ondes sismiques

Ce sont aussi des vagues de trois dimensions. Il y a principalement ceux de type P qui sont des vagues et des types de compression S Que sont les coupes ou les cisaillements (SEntendre en anglais).

Les vagues P ou les primaires sont les premiers à arriver car ils se propagent plus rapidement que les vagues S ou secondaire.

Sonner

Son en parlant

Le son est un type d'onde à trois dimensions. Ces vagues se sont propagées dans toutes les directions, bien que, comme nous l'avons déjà dit, pas avec la même intensité dans toutes les directions.

C'est parce que la source sonore n'émet pas toujours avec une symétrie parfaitement sphérique.

Les références

1. Baranek, L. 1969. Acoustique. 2e. Édition. McGraw Hill.
2. Griffiths G. Ondes linéaires et non linéaires. Récupéré de: Scholarpedia.org.
3. Nottoli, h. 2004. Physique appliquée à l'architecture. Nobuko.
4. Whitham g.B. 1999. Ondes linéaires et non linéaires. Wiley. 
5. Wikiwaves. Vagues non linéaires. Récupéré de: wikiwaves.org