Formules d'ondes stationnaires, caractéristiques, types, exemples

Le vagues debout Ce sont des vagues qui se propagent dans une moitié limitée, allant et venant dans une partie de l'espace, contrairement aux vagues itinérantes qui, lors de la propagation.

Ils sont à la base des sons produits dans les instruments de musique, car ils surviennent facilement sur les chaînes fixes, soit à l'un de ses extrémités, soit les deux. Ils sont également créés dans des membranes tendues telles que les tambours ou les tubes à l'intérieur et les structures telles que les ponts et les bâtiments.

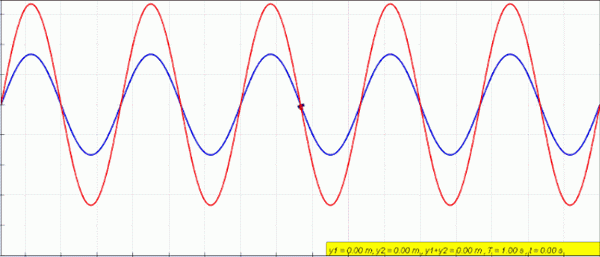Animation d'une onde stationnaire (rouge) créée par la superposition d'une gauche (bleue) et de la vague droite (vert). Source: Lookangmany Merci à l'auteur de Simulation original = Wolfgang Christian et Francisco Schembre Auteur de Easy Java Simulation = Francisco Schembre / CC BY-SA (https: // CreativeCommons.Org / licences / by-sa / 4.0)

Lorsque vous avez une corde fixe aux deux extrémités, comme une guitare, par exemple, les vagues sont créées avec une amplitude et une fréquence identiques, qui voyagent dans des sens opposés et combinent en produisant un phénomène appelé ingérence.

Si les vagues sont en phase, les crêtes et les vallées sont alignés et entraînent une onde avec une double amplitude. Dans ce cas, on parle d'interférence constructive.

Mais si les vagues qui interfèrent sont hors de phase, les crêtes de l'une rencontrent les vallées des autres et l'amplitude qui résulte est nul. C'est alors une interférence destructrice.

[TOC]

Formules et équations

Les principaux éléments de l'onde pour le représenter dans l'espace et le temps sont son amplitude A, sa longueur d'onde λ et sa fréquence angulaire ω.

Éléments d'une vague. Source: Wikimedia Commons.

En représentation mathématique, il est préféré utiliser k, que le Numéro d'onde O Nombre de fois que la vague par unité se produit. C'est pourquoi il est défini à travers la longueur de l'onde λ qui est la distance entre deux vallées ou deux crêtes:

K = 2π / λ

Tandis que le fréquence angulaire Il est lié à la période ou à la durée d'une oscillation complète, comme:

Ω = 2π / t

Et aussi la fréquence F est donnée par:

F = ω / 2π

Donc:

F = 1 / t

De plus, les vagues se déplacent avec vitesse V selon:

v = λ.F

Expression mathématique de la vague stationnaire

Mathématiquement, nous pouvons exprimer une vague à travers la fonction sinusale ou la fonction cosinus. Supposons qu'il y ait des ondes d'amplitude A égale, de la longueur d'onde λ et de la fréquence ω, se propageant le long d'une corde et dans des sens opposés:

et₁ = Un péché (kx - ωt)

et₂ = Un péché (kx + ωt)

Lorsque nous les ajoutons, nous trouvons la vague résultante et_R:

et_R = Y₁ + et₂ = A sen (kx - ωt) + a sin (kx + ωt)

Il existe une identité trigonométrique pour trouver la somme:

Peut vous servir: qu'est-ce que la rugosité relative et absolue?

sin α + sin β = 2 sin (α + β) / 2 . cos (α - β) / 2

À travers cette identité, l'onde résultante et_R est laissé:

et_R = [2a Sen Kx] . cos ωt

Emplacement des nœuds et du ventre

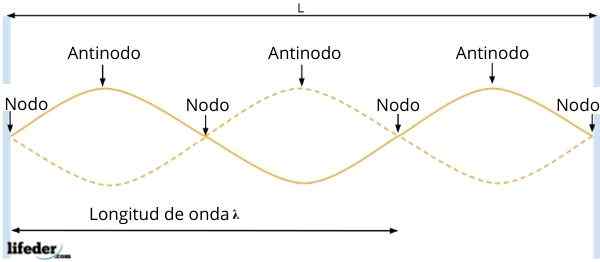Antinodos ou ventre et nœuds

L'onde résultante a une amplitude à_R = 2ase kx, qui dépend de la position de la particule. Ensuite, aux points pour lesquels Sen Kx = 0, l'amplitude de l'onde est annulée, c'est-à-dire qu'il n'y a pas de vibration.

Ces points sont:

Kx = π, 2π, 3π ..

Comme k = 2 π / λ:

(2 π / λ) x = π, 2π, 3π ..

x = λ / 2, λ, 3λ / 2 ..

Dans de tels points, une interférence destructrice se produit et ils sont appelés nœuds. Ils sont séparés par une distance égale à λ / 2, comme déduit du résultat précédent.

Et entre deux nœuds consécutifs sont les antinodos ou ventre, dans lequel l'amplitude de l'onde est maximale, car l'interférence constructive se produit. Ils se produisent quand:

sin kx = ± 1

Kx = ± π / 2, 3π / 2, 5π / 2 ..

Encore une fois k = 2 π / λ puis:

x = λ / 4, 3λ / 4, 5λ / 4, ..

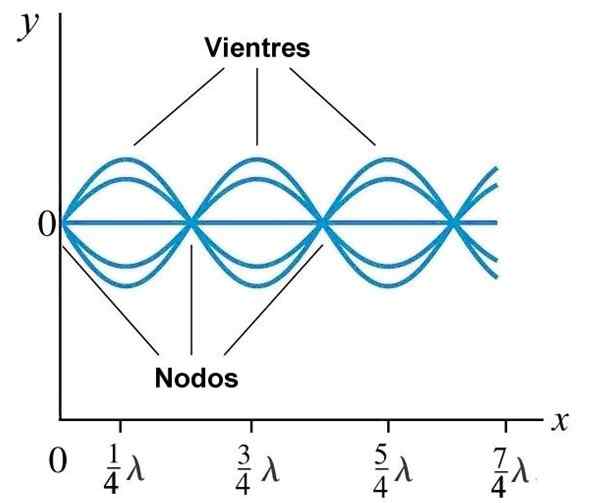Ventre ou antinodes et nœuds dans une onde stationnaire générée sur une corde avec une extrémité fixe à x = 0. Source: Wikimedia Commons.

Modes normaux sur une corde

Les conditions de bordure sur la corde déterminent comment sont les longueurs d'onde et les fréquences. Si une corde en longueur L est fixée par ses deux extrémités, elle ne peut pas vibrer avec une fréquence, car les points où la corde est fixée sont déjà des nœuds.

Además la separación entre nodos adyacentes es λ/2, y entre nodo y vientre es λ/4, de esta manera solamente para ciertas longitudes de onda se producen ondas estacionarias: aquellas en las que se ajusta un número entero n de λ/2 dentro du:

(λ / 2) = l, avec n = 1, 2, 3, 4 .. .

Donc:

λ = 2l / n

Les harmoniques

Les différentes valeurs prises λ sont appelées harmonique. Ainsi nous avons:

-Première harmonique: λ = 2l

-Deuxième harmonique: λ = l

-Troisième harmonique: λ = 2 l / 3

-Salle harmonique: λ = l / 2

Et ainsi de suite.

Vitesse et fréquence

Bien que l'onde stationnaire ne semble pas bouger, l'équation est toujours valable:

v = λ. F

Donc:

V = (2L / N) . F

F = nv / 2l

Maintenant, il peut être démontré que la vitesse avec laquelle une onde se déplace dans une corde dépend de la tension t dans la même et de sa densité linéaire de masse μ (masse par unité de longueur) comme:

Donc:

Peut vous servir: charges mortes: caractéristiques, calcul, exemples

Caractéristiques des vagues stationnaires

-Lorsque les vagues sont fixes, l'onde résultante ne se propage pas comme ses composants, qui vont d'un endroit à un autre. Il y a des points où y = 0 parce qu'il n'y a pas de vibration: les nœuds, en d'autres termes, l'amplitude à_R C'est nul.

-L'expression mathématique d'une onde stationnaire se compose du produit d'une partie spatiale (qui dépend de la coordonnée X ou des coordonnées spatiales) et d'une partie temporelle.

-Parmi les nœuds, la vague noire qui en résulte oscille en un endroit, tandis que les vagues qui vont d'un endroit à un autre y sont obsolètes.

-Juste dans les nœuds, l'énergie n'est pas transportée, car cela est proportionnel au carré de l'amplitude, mais est piégé entre les nœuds.

-La distance entre les nœuds adjacents est la moitié de la longueur d'onde.

-Les points auxquels la corde est fixée est également considérée comme des nœuds.

Gars

Vagues stationnaires dans une dimension

Les vagues dans une corde fixe sont des exemples d'ondes stationnaires dans une dimension, dont la description mathématique que nous avons proposée dans les sections précédentes.

Vagues stationnaires en deux et trois dimensions

Les ondes stationnaires peuvent également être présentées en deux et trois dimensions, étant une description mathématique légèrement plus complexe.

Exemples de course ondas

Cordes fixes

-Une chaîne fixée par l'extrême qui est oscillée à la main ou avec un piston par l'autre génère des vagues stationnaires sur toute sa longueur.

Instruments de musique

Des vagues stationnaires sont créées dans des instruments de musique tels que ViolonCello. Source: Pixabay.

-Lorsque vous jouez des instruments à cordes tels que la guitare, la harpe, le violon et le piano.

Des ondes stlover sont également créées dans des tubes à air, comme les tubes d'organe.

Bâtiments et ponts

Des vagues stationnaires surviennent dans des structures telles que les ponts et les bâtiments. Un cas remarquable était celui du pont de suspension Tacoma Narrows près de la ville de Seattle, États-Unis. Peu de temps après avoir été inauguré en 1940, ce pont s'est effondré en raison des vagues stationnaires créées à l'intérieur du vent.

La fréquence du vent correspond à la fréquence naturelle du pont, créant en vagues stationnaires en ceci, qui augmentaient leur amplitude jusqu'à ce que le pont s'effondre. Le phénomène est connu sous le nom de résonance.

Il peut vous servir: réflexion légère

Seich

Dans les ports, il y a un phénomène très curieux appelé Seiche, dans lequel les vagues de la mer produisent de grandes oscillations. En effet.

Les eaux portuaires se déplacent avec leur propre fréquence, ainsi que celles de l'océan. Si les deux eaux correspondent à leurs fréquences, il y a une grande vague stationnaire en raison de la résonance, comme cela s'est produit avec le pont Tacoma.

Les Seich Ils peuvent également se produire dans les lacs, les réservoirs, les piscines et d'autres plans d'eau limités par des surfaces.

Réservoirs de poisson

Des vagues stationnaires peuvent être créées dans un bol à poisson transporté par une personne, si la fréquence à laquelle la personne est égale à la fréquence de la balançoire de l'eau.

Exercice résolu

La corde de guitare a l = 0.9 m et densité de pâte linéaire μ = 0.005 kg / m. Il est soumis à 72 N de tension et son mode de vibration est celui qui montre la figure, avec Amplitude 2A = 0.5 cm.

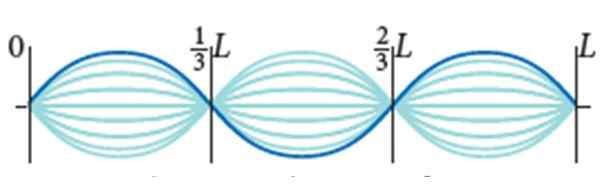Vagues stationnaires sur une corde de guitare. Source: Bauer, W. Physique.

Trouver:

a) vitesse de propagation

b) Fréquence des vagues

c) l'équation des ondes stationnaires correspondantes.

Solution à

À travers:

Est obtenu;

V = [72 n / (0.005 kg / m)]^1/2  = 120 m / s.

Solution B

La distance entre deux nœuds adjacents est λ / 2, donc:

(2/3) l - (1/3) l = λ / 2

(1/3) l = λ / 2

λ = 2l / 3 = 2 x 0.90 m / 3 = 0.60 m.

Comme v = λ.F

F = (120 m / s) / 0.60 m = 200 s^-1= 200 Hz.

Solution C

L'équation est:

et_R = [2a Sen Kx] . cos ωt

Nous devons remplacer les valeurs:

K = 2π / λ = k = 2π / 0.60 m = 10 π / 3

F = ω / 2π

Ω = 2π x 200 Hz = 400 π Hz.

L'amplitude 2A est déjà donnée par la déclaration:

2a = 0.5 cm = 5 x 10 ^-3 m.

Donc:

et_R = 5 x 10 ^-3 m . sin [(10π / 3) x] . cos (400πt) =

= 0.5 cm . sin [(10π / 3) x] . cos (400πt)

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
2. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 7. Vagues et physique quantique. Édité par Douglas Figueroa (USB).
3. Giancoli, D.  2006. Physique: principes avec applications. 6e. Ed Prentice Hall.
4. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Élégant. Cengage Learning.
5. Tipler, P. (2006) Physique de science et de technologie. 5e ed. Volume 1. Éditorial Revered.
6. Wikipédia. Seiche. Récupéré de: est.Wikipédia.org.