Caractéristiques des vagues sénoïdes, pièces, calcul, exemples

Le vagues sinusoïdales Ce sont des modèles d'onde qui peuvent être décrits mathématiquement par les fonctions sinus et cosinus. Ils décrivent à juste titre des événements naturels et des signes variables dans le temps, tels que les tensions générées par les usines électriques, puis utilisées dans les maisons, les industries et les rues.

Des éléments électriques tels que les résistances, les condensateurs et les inductances, qui se connectent aux entrées de tension sinusoïdale, produisent également des réponses également sinusoïdales. Les mathématiques utilisées dans leur description sont relativement simples et ont été entièrement étudiées.

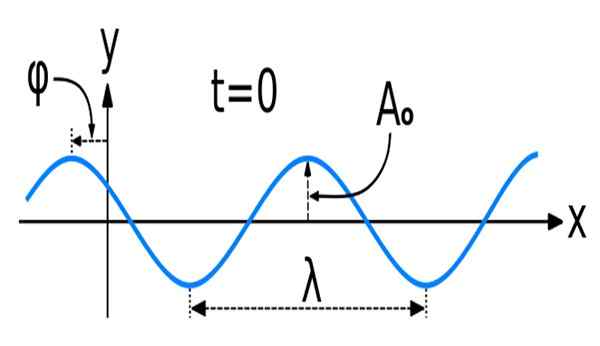
Figure 1. Une onde sinusoïdale avec certaines de ses principales caractéristiques spatiales: amplitude, longueur d'onde et phase. Source: Wikimedia Commons. Wave_new_sine.SVG: Kraaiennestoriginal comme une vague de cosinus, par l'utilisateur: pelegs, comme fichier: wave_new.Svgderivative Work: Dave3457 [CC BY-SA 3.0 (https: // CreativeCommons.Org / licences / by-sa / 3.0)]

Les mathématiques des ondes sinusoïdales ou sinusoïdales, comme on les connaît également, est celle des fonctions sinus et cosinus.

Ce sont des fonctions répétitives, ce qui signifie la périodicité. Les deux ont la même manière, avec la prévoyance que le cosinus est déplacé à gauche par rapport à la poitrine dans une salle cyclable. Il est observé dans la figure 2:

Figure 2. Les fonctions Sen X et Cos X sont déplacées l'une par rapport à l'autre. Source: F. Zapata.

Alors cos x = sin (x + π / 2). À l'aide de ces fonctions, une onde sinusoïdale est représentée. Pour ce faire, l'ampleur en question est placée sur l'axe vertical, tandis que dans l'axe horizontal, le temps est situé.

La qualité répétitive de ces fonctions est également appréciée sur le graphique ci-dessus: le motif est répété en continu et régulièrement. Grâce à ces fonctions, vous pouvez exprimer des tensions et des courants du type sinien variant dans le temps, en plaçant sur l'axe vertical au lieu du et, ongle V ou un Toi pour représenter la tension ou le courant, et sur l'axe horizontal au lieu du X, Le t du temps.

La façon la plus générale d'exprimer une onde sinusoïdale est:

v (t) = v_m péché (Ωt + φ)

Ensuite, nous approfondirons la signification de cette expression, définissant certains termes de base afin de caractériser l'onde sinusoïdale.

[TOC]

Des soirées

La période, l'amplitude, la fréquence, le cycle et la phase sont des concepts s'appliquent aux ondes périodiques ou répétitives et sont importants pour les caractériser correctement.

Période

Une fonction périodique telle que celles mentionnées, qui se répète à intervalles réguliers, répond toujours à la propriété suivante:

f (t) = f (t + t) = f (t + 2t) = f (t + 3t) =… .

Où T C'est un montant appelé vague, Et c'est le temps qu'il faut pour répéter une phase de même. Dans les unités de système international, la période est mesurée en quelques secondes.

Amplitude

Selon l'expression générale de la vague sénoïde v (t) = v_m sin (ωt + φ), v_m C'est la valeur maximale de la fonction, qui se produit lorsque sin (ωt + φ) = 1 (Se rappeler que la plus grande valeur que la fonction sinusale et cosinus admet les deux est 1). Cette valeur maximale est précisément le Amplitude des vagues, aussi connu sous le nom amplitude maximale.

En cas de tension sera mesuré en volts et s'il s'agit d'un courant, il sera en ampères. Dans l'onde sinusoïdale, la largeur est constante, mais dans d'autres types d'onde, l'amplitude peut varier.

Peut vous servir: Thermomètre de résistance: caractéristiques, fonctionnement, utilisations

Cycle

C'est une partie de la vague contenue dans une période. Dans le chiffre précédent, la période a été prise en la mesurant à partir de deux pics ou crêtes consécutifs, mais il peut commencer à être mesuré à partir d'autres parties de la vague, alors qu'ils sont limités par une période.

Remarque dans la figure suivante car un cycle couvre d'un point à un autre avec la même valeur (hauteur) et la même pente (inclination).

figure 3. Dans une vague sinusoïdale, un cycle se déroule toujours pendant une période. L'important est que le point de départ et la fin sont à la même hauteur. Source: Boylestad. Introduction à l'analyse des circuits. Pearson.

Fréquence

C'est la quantité de cycles qui se produisent en 1 seconde et sont liées à l'argument de la fonction sinusale: Ωt. La fréquence est indiquée comme F Et il est mesuré en cycles par seconde ou Hertz (Hz) dans le système international.

La fréquence est donc la quantité inverse de la période:

F = 1 / t

Pendant la fréquence F est lié au Fréquence angulaire ω (pulsation) comme:

Ω = 2πF

La fréquence angulaire est exprimée en radianes / seconde dans le système international, mais les radians sont sans dimension, donc la fréquence F et fréquence angulaire Ω Ils ont les mêmes dimensions. Notez que le produit Ωt donne des radians en conséquence et doit être pris en compte lors de l'utilisation de la calculatrice pour obtenir la valeur de Sen ωt.

Phase

Il correspond au déplacement horizontal ressenti par la vague, par rapport à un temps pris comme référence.

Dans la figure suivante, l'onde verte est avancée par rapport au rouge dans un temps t_d. Deux vagues sinusoïdales sont en phase Lorsque votre fréquence et votre phase sont les mêmes. Si la phase diffère, alors ils sont dans écart. La figure 2 ondes sont également obsolètes.

Figure 4. Vagues sinusides pelues. Source: Wikimedia Commons. Aucun auteur lisible par machine fourni. Kanjo ~ Commonswiki a supposé (sur la base des réclamations du droit d'auteur). [Domaine public].

Si la fréquence des vagues est différente, elles seront en phase lorsque la phase ωt + φ être le même dans les deux vagues à certains moments.

Générateur d'ondes sénoïdes

Il existe de nombreuses façons d'obtenir un signal en forme de sinus. Les ruisseaux faits maison les fournissent.

Application de la loi de Faraday

Un moyen assez simple d'obtenir un signal sinusoïdal est d'utiliser la loi de Faraday. Cela indique que dans un circuit fermé de courant, par exemple une boucle, placé au milieu d'un champ magnétique, un courant induit est généré lorsque l'écoulement du champ magnétique change dans le temps. Par conséquent, un Tension induite soit induit.

Le flux du champ magnétique varie si la boucle est tournée avec une rapidité angulaire constante au milieu du champ créé entre les pôles n et s de l'aimant illustré sur la figure.

Peut vous servir: Neptune (planète)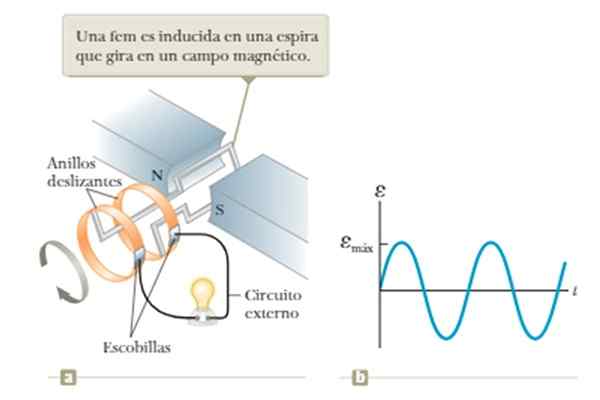Figure 5. Générateur de vagues basé sur la loi d'induction de Faraday. Source: Source: Raymond A. Seway, Jonh W. Jewett [cc by-sa 4.0 (https: // CreativeCommons.Org / licences / by-sa / 4.0)].

La limitation de cet opérateur est la dépendance à la tension obtenue avec la fréquence de rotation de la boucle, comme on le verra plus en détail dans l'exemple 1 de la section Exemples ultérieurement.

Oscillateur Wien

Une autre façon d'obtenir une onde sinusoïdale, cette fois avec un électron. De cette façon, les ondes sinusoïdales sont obtenues dont la fréquence et l'amplitude peuvent modifier en fonction de leur commodité, au moyen du réglage du commutateur.

La figure montre un générateur de signal sinusoïdal, avec lequel d'autres formes d'onde peuvent également être obtenues: triangulaire et carrés entre autres.

Figure 6. Un générateur de signaux. Source: Source: Wikimedia Commons. Opgreg chez anglais wikipedia [CC BY-SA 3.0 (https: // CreativeCommons.Org / licences / by-sa / 3.0)].

Comment calculer les ondes sinusoïdales?

Pour effectuer des calculs qui impliquent des ondes sinusoïdales, une calculatrice scientifique est utilisée qui a les fonctions trigonométriques des sinus et en cosinus, ainsi que son inverse. Ces calculatrices ont des modes pour travailler les angles en degrés ou en rayons, et il est facile de convertir une façon à l'autre. Le facteur de conversion est:

180 º = π Radia.

Selon le modèle de calculatrice, vous devez naviguer via la touche de mode pour trouver l'option de degré, qui vous permet de travailler sur les fonctions trigonométriques en degrés, ou l'option RAD, pour travailler directement les angles dans les radians.

Par exemple le péché 25 º = 0.4226 avec la calculatrice mis en mode deg. En convertissant 25 º en rayons, vous obtenez 0.4363 Radianes et Sen 0.4363 rad = 0.425889 ≈ 0.4226.

L'oscilloscope

L'oscilloscope est un appareil qui permet de visualiser sur un écran de signes de tensions et de courants alterne et direct. Il a des boutons pour ajuster la taille du signal sur une grille comme indiqué dans la figure suivante:

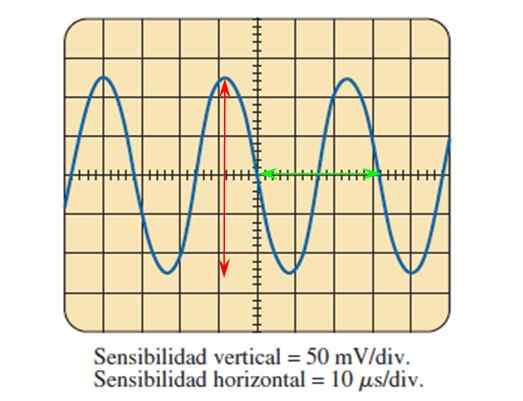Figure 7. Un signal sinusoïdal mesuré avec un oscilloscope. Source: Boylestad.

Grâce à l'image fournie par l'oscilloscope et en connaissant le réglage de la sensibilité dans les deux axes, il est possible de calculer les paramètres d'onde décrits ci-dessus.

Peut vous servir: Galaxies elliptiques: formation, caractéristiques, types, exemples

La figure montre le signal de tension sinusoïdale en fonction du temps, dans lequel chaque division de l'axe vertical vaut 50 millibolts, tandis que dans l'axe horizontal, chaque division vaut 10 microsecondes.

L'amplitude pic à pic compte les divisions que l'onde englobe verticalement, aidant à la flèche rouge:

5 Les divisions sont comptées à l'aide de la flèche rouge, de sorte que la tension de pic-pico est:

V_pp = 5 divisions x 50 mV / division = 250 mV.

Tension pico V_p Il est mesuré à partir de l'axe horizontal, étant de 125 mV.

Pour trouver la période, un cycle est mesuré, par exemple celui délimité par la flèche verte, qui couvre 3.2 divisions, alors la période est:

T = 3.2 divisions x 10 microsecondes / division = 32 microsecondes = 32 μs

Exemples

Exemple 1

Pour le générateur de la figure 3, démontrez à partir de la loi de Faraday que la tension induite a un sinus. Supposons que la boucle se compose de n tours au lieu d'un, le tout avec la même zone A et tourne avec une rapidité angulaire constante ω au milieu d'un champ magnétique B uniforme.

Solution

La loi de Faraday dit que la FEM induite ε est:

ε = -n (dφ_B / dt)

Où Φ_B C'est le flux du champ magnétique, qui sera variable, car cela dépend de la façon dont la boucle est exposée au champ à chaque instant. Le signe négatif décrit simplement le fait que cette FEM s'oppose à la cause qui le produit (Loi de Lenz). L'écoulement dû à une seule boucle est:

Φ_B = B.POUR.cos θ

θ est l'angle que le vecteur normal au plan de la boucle se forme avec le champ B Au fur et à mesure que la rotation a lieu (voir figure), cet angle varie naturellement comme:

θ = Ωt

De manière que: Φ_B = B.POUR.cos θ = b.POUR.cos Ωt. Maintenant, il vous suffit de dériver cette expression par rapport au temps et avec elle la FEM induite est obtenue:

ε = -n.D (B.POUR.cos ωt) / dt

Comme le champ B Il est uniforme et la zone spase ne varie pas, ils quittent le dérivé:

ε = -nba. D (cos ωt) / dt = ωnba. Sen Ωt

Exemple 2

Une boucle a une superficie de 0.100 m² et se tourner vers 60.0 REV / S, avec son axe de rotation perpendiculaire à un champ magnétique uniforme de 0.200 T. Sachant que la bobine a 1000 tours à trouver: a) la FEM maximale générée, b) l'orientation de la bobine par rapport au champ magnétique lorsque la FEM induite maximale se produit.

Figure 8. Une spirale de n tours brisés au milieu d'un champ magnétique uniforme et génère un signal sinusoïdal. Source: R. Serow, physique pour la science et l'ingénierie. 2ieme volume. Cengage Learning.

Solution

a) le maximum FEM est ε_Max = Ωnba

Avant de procéder pour remplacer les valeurs, la fréquence de 60 REV / s aux unités du système international doit être transmise. Il est connu que 1 révolution équivaut à un tour ou à 2p radianes:

60.0 REV / S = 120p Radianes / S

ε_Max = 120p Radianes x 1000 Laps x 0.200 t x 0.100 m² = 7539.82 V = 7.5 kV

b) Lorsque cette valeur se produit Sen ωt = 1 donc:

ωt = θ = 90º,

Dans ce cas, le plan en spirale est parallèle à B, de sorte que le vecteur normal dans ledit plan forme à 90º avec le champ. Cela se produit lorsque le vecteur noir de la figure 8 est perpendiculaire au vecteur vert qui représente le champ magnétique.

Les références

1. Boylestad, R. 2011. Introduction à l'analyse des circuits. 12e. Édition. Pearson. 327-376.
2. Figueroa, D. 2005. Électromagnétisme. Série physique pour la science et l'ingénierie. Volume 6. Édité par D. FigUeroa. Université Simon Bolivar. 115 et 244-245.
3. Figueroa, D. 2006. Laboratoire de physique 2. Équinoxe éditorial. 03-1 et 14-1.
4. Vagues sinusoïdales. Récupéré de: iessierradegara.com
5. SERAY, R. 2008.Physique pour la science et l'ingénierie. 2ieme volume. Cengage Learning. 881-884