Nombres parfaits comment les identifier et les exemples

UN Le nombre parfait est un nombre naturel tel que La somme de ses diviseurs est la même que le nombre. De toute évidence, il ne peut pas être inclus parmi les diviseurs du numéro lui-même.

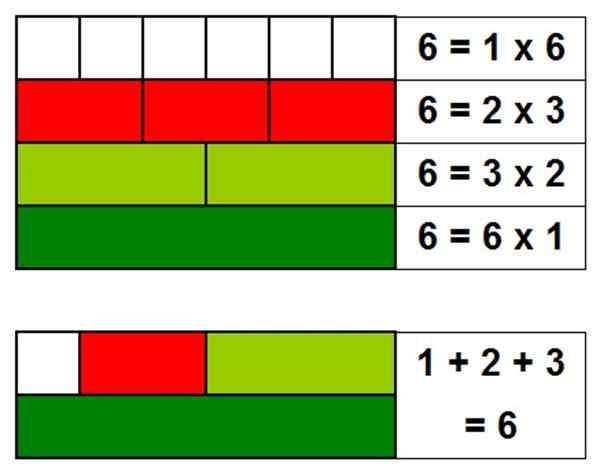
L'un des exemples les plus simples de nombre parfait est 6, car ses diviseurs sont: 1, 2 et 3. Si nous ajoutons les diviseurs, il est obtenu: 1 + 2 + 3 = 6.

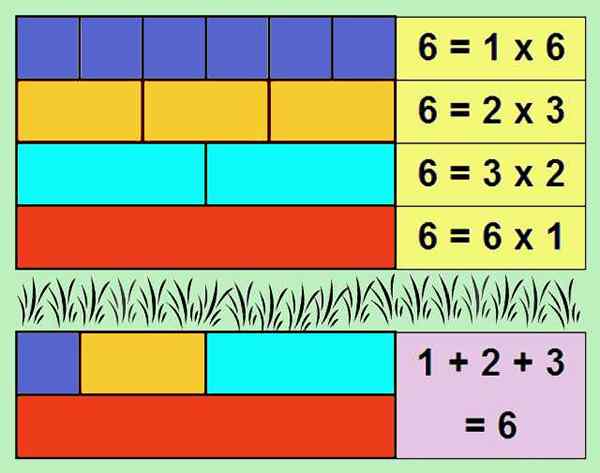Figure 1. Le nombre 6 est parfait, car la somme de ses diviseurs, sans compter le nombre lui-même, donne le numéro 6. Source: auto-faite

La somme des diviseurs d'un entier, sans compter le nombre lui-même, est appelée aliquote. Par conséquent, un nombre parfait est égal à son aliquote.

Mais si dans la somme des diviseurs d'un nombre, le nombre lui-même est inclus, alors un nombre parfait sera celui que la somme de tous ses diviseurs divisée par 2 est égal au nombre lui-même.

[TOC]

Histoire

Les mathématiciens de l'antiquité, en particulier les Grecs, ont accordé une grande importance aux nombres parfaits et aux qualités divines attribuées.

Par exemple, Philo de Alejandría, vers le 1er siècle, a affirmé que 6 et 28 sont des nombres parfaits qui coïncident avec les six jours de la création du monde et les vingt-huit jours qu'il faut pour que la lune tourne la terre.

Les nombres parfaits sont également présents dans la nature, par exemple dans le pôle Nord de Saturne apparaît également le numéro 6 parfait, un vortex en forme d'hexagone trouvé par la sonde Cassini et qui a intrigué les scientifiques. 

Les abeilles en nid d'abeilles ont des cellules sous forme hexagonale, c'est-à-dire avec 6 côtés.  Il est montré que le polygone avec le numéro 6 parfait est celui qui permet de maximiser le nombre de cellules dans la ruche des abeilles, avec la cire minimale pour son élaboration.

Figure 2. Le numéro 6 parfait est présent dans les abeilles en nid d'abeilles. Il est montré qu'avec ce nombre de côtés, la quantité de cire à utiliser pour former les cellules est minime. Source: Pixabay.

Propriétés de nombres parfaits

La somme de tous les diviseurs d'un nombre naturel n est indiquée par σ (n). Dans un nombre parfait, il est vrai que: σ (n) = 2n.

Formule et critères d'Euclide

Euclid a découvert une formule et un critère qui vous permet de trouver les nombres parfaits. Cette formule est:

2^(N-1) (2ⁿ -1)

Cependant, le nombre généré par la formule ne sera parfait que lorsque le facteur (2ⁿ -1) être cousin.

Peut vous servir: composants rectangulaires d'un vecteur (avec des exercices)

Voyons comment les premiers numéros parfaits sont générés:

Si n = 2 alors nous en avons 2¹ (2² - 1) = 2 x 3 = 6 que nous avons déjà vu qu'il est parfait.

Quand n = 3 vous en avez 2² (2³ - 1) = 4 x 7 = 28 Ce qui est également parfait tel qu'il est vérifié en détail dans l'exemple 1.

Voyons ce qui se passe avec n = 4. En remplaçant dans la formule Euclide, nous avons:

2³ (2⁴ - 1) = 8 x 15 = 120

Il peut être vérifié que ce nombre n'est pas parfait, comme illustré en détail dans l'exemple 3. Cela ne contredit pas les critères d'Euclide, car 15 n'est pas un cousin, une exigence nécessaire pour que le résultat soit un nombre parfait.

Voyons ce qui se passe quand n = 5. Appliquer la formule que nous avons:

2⁴ (2⁵ - 1) = 16 x 31 = 496

Comme 31 est un nombre premier, le numéro 496 doit donc être parfait, selon les critères d'Euclide. Dans l'exemple 4, il est montré en détail qu'il est effectivement.

Les nombres premiers qui ont le formulaire 2^p - 1 Ils sont appelés cousins ​​de Mersenne, en l'honneur du moine Marin Mersenne, qui a étudié les nombres premiers et les nombres parfaits au XVIIe siècle.

Par la suite, au XVIIIe siècle, Leonhard Euler a montré que tout le nombre parfait généré par la formule Euclide est des paires.

À ce jour, un parfait a été trouvé qui est étrange.

Le plus grand nombre parfait connu

À la date actuelle, 51 nombres parfaits sont connus, tous générés par la formule et les critères Euclide. Ce nombre a été obtenu une fois que le cousin de Mersenne a été trouvé, c'est-à-dire: (2^82589933 - 1).

Le numéro parfait n ° 51 est (2^82589933) X (2^82589933 - 1) et a 49724095 digitos.

Un nombre parfait est ami de vous-même

Dans la théorie des nombres, il est dit que deux nombres sont amis lorsque la somme des diviseurs de l'un, sans compter le nombre lui-même, est égale à l'autre nombre et vice versa.

Il peut vous servir: segment de ligne et semi-rovi

Le lecteur peut vérifier que la somme des diviseurs de 220, sans compter le 220 est 284. En revanche, la somme des diviseurs de 284, sans 284, est égale à 220. Par conséquent, les chiffres, les couples 220 et 284, sont amis.

De ce point de vue, un nombre parfait est ami de vous-même.

Exemples de nombres parfaits

Ensuite, les huit premiers numéros parfaits sont répertoriés:

6

28

496

8128

33550336

8589869056

137438691328

2305843008139952128

Exercices

Dans les exercices suivants, il sera nécessaire de calculer les diviseurs d'un nombre, puis de faire leur somme et de vérifier si le nombre est un numéro parfait ou non.

Par conséquent, avant de traiter les exercices, nous examinerons le concept et montrerons comment ils sont calculés.

Pour commencer, vous devez vous rappeler que les nombres peuvent être des cousins ​​(lorsqu'ils ne peuvent être divisés qu'en exact avec eux-mêmes et 1) ou des composés (lorsqu'ils peuvent se décomposer comme produit de nombres premiers).

Pour un numéro de composé, vous avez:

N = aⁿ . b^m. c^p … R^k 

Où a, b, c ... r sont des nombres premiers et n, m, p ... k sont des représentants appartenant à des nombres naturels, qui peuvent valoir à partir de 1.

En termes de ces représentants, il existe une formule pour savoir combien de diviseurs le nombre N a, bien qu'il ne nous dise pas ce que ce sont. Soit C ce montant, alors:

C = (n +1) (m +1) (p +1) ... (k +1)

La décomposition du nombre n comme produit de nombres premiers et la connaissance du nombre de diviseurs, à la fois cousins ​​et non-cousins, nous aideront à déterminer quels sont ces diviseurs.

Une fois tout le monde, sauf le dernier qui n'est pas requis dans la somme, il peut être vérifié s'il s'agit d'un nombre parfait ou non.

- Exercice 1

Vérifiez que le numéro 28 est parfait.

Solution

Le premier sera de décomposer le nombre dans ses facteurs premiers.

28 | 2
14 | 2
07 | 7
01 | 1

Ses diviseurs sont: 1, 2, 4, 7, 14 et 28. Si nous excluons le 28, la somme des diviseurs donne:

Peut vous servir: moitié de 15

1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28

Par conséquent, le 28 est un nombre parfait.

De plus, la somme de tous ses diviseurs est de 28 + 28, donc la règle σ (28) = 2 x 28.

- Exercice 2

Décidez si le numéro 38 est parfait ou non.

Solution

Le nombre est décomposé en ses facteurs premiers:

39 | 3
13 | 13
01 | 1

Les diviseurs de 39 sans inclure le nombre eux-mêmes sont: 1, 3 et 13. Somme 1 + 3 + 13 = 4 + 13 = 17 n'est pas égal à 39, donc 39 est un numéro imparfait ou non perfection. 

- Exercice 3

Découvrez si le numéro 120 est parfait ou imparfait.

Solution

Le nombre est décomposé en ses facteurs premiers:

120 | 2
060 | 2
 30 | 2
 15 | 3
  5 | 5
  1 | 1

D'après les facteurs premiers, les diviseurs se trouvent:

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 et 120

Si 120 étaient parfaits lors de l'ajout de tous ses diviseurs devraient être obtenus 2 x 120 = 240. 

1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360

Ce résultat est clairement différent de 240, il est donc conclu que le nombre 120 n'est pas un nombre parfait.

- Exercice 4

Vérifiez que le nombre 496, obtenu par les critères Euclide, est un nombre parfait.

Solution

Le numéro 496 est décomposé en ses principaux facteurs:

496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1

Ensuite, leurs diviseurs sont:

1, 2, 4, 8, 16, 31, 62, 124, 248, 496

Maintenant, tous sont ajoutés, sauf 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Confirmant que c'est en effet un nombre parfait.

Les références

1. Baldor, un. 1986. Arithmétique. Éditions et distributions Codex.
2. Tout sur les nombres premiers. Nombres d'amis. Récupéré de: infirmière.org.
3. Wolfram Mathworld. La règle d'Euler. Récupéré de: Mathworld.Wolfram.com.
4. Wolfram Mathworld. Nombre parfait. Récupéré de: Mathworld.Wolfram.com.
5. Wikipédia. Nombres parfaits. Récupéré de: dans.Wikipédia.org.
6. Wikipédia. Nombres d'amis. Récupéré de: est.Wikipédia.org.