Angles et triangles

Les angles et les triangles font partie de la géométrie plate. Volet

Quels sont les angles et les triangles?

UN angle C'est la région de l'avion délimité par deux semi-sortants avec un point d'origine en commun. Ce point est connu comme le sommet, tandis que la semi-sort est appelée côtés. D'un autre côté, un Triangle C'est une figure de trois angles et de trois côtés, avec trois sommets.

Nous parlerons d'abord des angles.

Angle

Il existe plusieurs façons de désigner les angles: à travers des lettres grecques telles que α, β, γ, à laquelle un accent circonflexe peut être ajouté; avec des majuscules rembourrés ou minuscules, a, b, c, a, b, c; des nombres, tels que 1, 2, 3 ... ou en utilisant le symbole d'angle ∠.

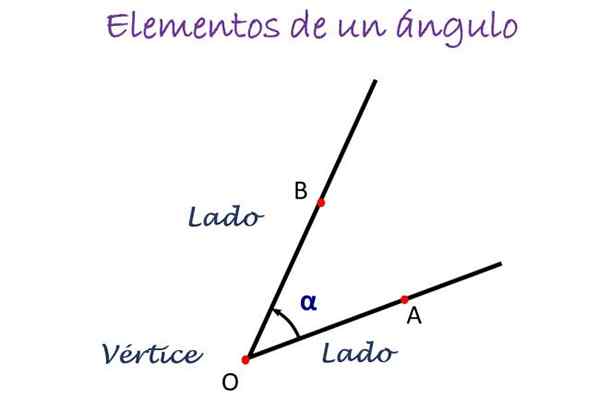Les principaux éléments d'un angle. Source: F. Zapata

Dans la figure ci-dessus, l'angle est mesuré du côté A à B, indiqué par la direction de la flèche, et au centre la lettre qui indique que le sommet est placé, qui est normalement ou. L'angle est ensuite désigné comme ∠ AOB.

Lorsque l'angle est mesuré dans un sens antihorarium, un signe + est arbitrairement attribué, et s'il est mesuré dans un horaire, un signe pour les distinguer.

La mesure des angles est réalisée au moyen d'un transporteur, qui se compose d'une feuille de plastique semi-circulaire comme celle illustrée ci-dessous. Le demi-cercle est divisé en 180 parties égales, chaque appel degré.

Pour mesurer, le sommet de l'angle est coïncidé avec le point central du transporteur, indiqué avec la flèche, et le côté initial avec l'un des bords, interne ou externe. Le dernier côté croise certaines des marques du transporteur, cette mesure étant l'angle.

Peut vous servir: Règle empirique: comment l'appliquer, à quoi sert-il, des exercices résolus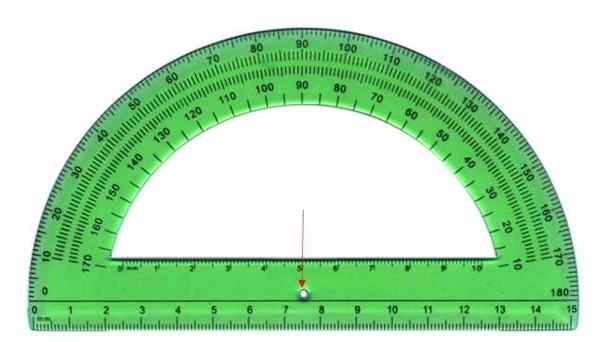Le convoyeur est l'instrument pour mesurer les angles. Source: Wikimedia Commons

Types d'angles

L'un des critères les plus utilisés pour classer les angles, est selon sa mesure. Par conséquent, un angle peut être:

• Nul, Mesures 0º.
• Pointu, dont la mesure se situe entre 0 et 90º.
• Droit, Il mesure exactement 90º.
• Obtus, Il est supérieur à 90 ° et moins de 180º.
• Plat, Sa mesure est égale à 180º.
• Complet, représente un virage complet et mesure 360º.

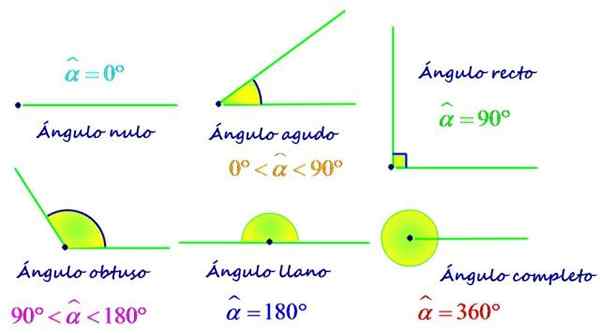Types d'angles selon votre mesure. Source: F. Zapata.

Selon la relation entre sa mesure et celle de l'angle plat, qui est de 180 °, les angles peuvent également être classés comme:

• Concave, S'il mesure moins de 180º. Par conséquent, les angles aigus, droits et obtus sont concaves, car sa mesure est toujours inférieure à 180 ° (voir la figure ci-dessus).
• Convexe, Si votre mesure est supérieure à 180º, comme les angles de 270 ° et 360 °.

Angles selon la somme de leurs mesures et selon la position de leurs côtés

Deux angles ∠ A et ∠ B peuvent être:

• Complémentaire, Si la somme de ses mesures est égale à 90º.
• Supplémentaire, Lors de l'ajout des mesures respectives, 180º est obtenu.
• Conjugué, Si cette somme est égale à 360º.

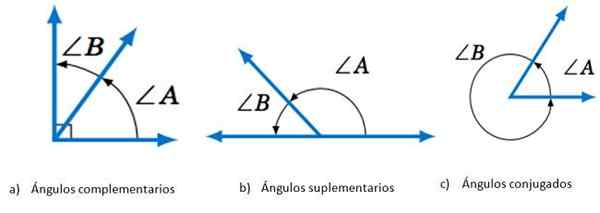Angles selon la somme de ses mesures. Source: Mathematics Libreretsxts.

Quant à la position de leurs côtés, deux angles peuvent être:

• Dans une rangée, Lorsque le sommet et l'un des côtés ont en commun.
• Adjacent, S'ils sont consécutifs, mais les côtés non communs sont opposés, ils sont également supplémentaires.
• Opposé par le sommet, Quand ils ont le sommet commun, et les côtés des angles sont prolongés dans la direction opposée.

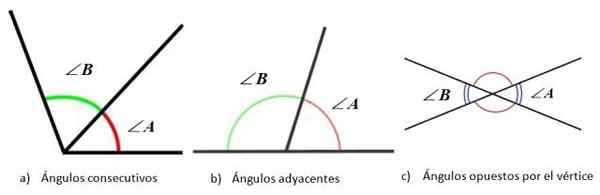Angles selon la position relative entre ses côtés. Source: F. Zapata

Triangles

Le triangle est une figure géométrique plate et fermée, appartenant à la famille des polygones, avec trois côtés composés de lignes qui sont coupées de deux à deux, générant trois angles.

Il peut vous servir: fonction de bijjectif: qu'est-ce que c'est, comment se fait-il, des exemples, des exercices

Ses éléments de base sont:

• Sommets, qui sont les points d'intersection des lignes susmentionnées.
• Côtés, un total de 3 et qui se composent des segments de lignes qui se connectent aux sommets.
• Angles internes, Également en nombre de 3, dont la somme est toujours égale à 180º.

Généralement, les côtés sont désignés avec des lettres latines minuscules, les sommets avec des majuscules et les angles avec des lettres grrielles minuscules, mais d'autres notations sont également possibles.

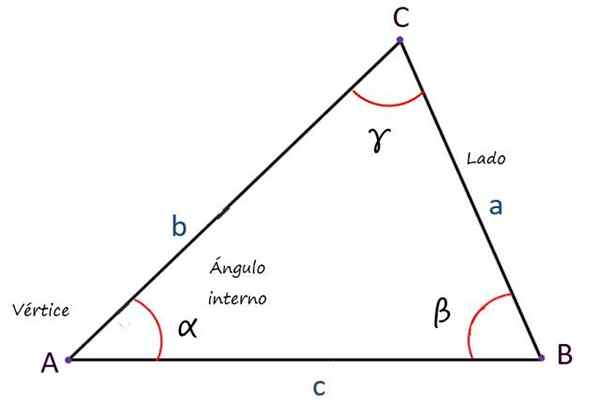Éléments principaux d'un triangle. Source: F. Zapata

Types de triangles

Triangles selon la forme de ses côtés

Selon ce critère, les triangles peuvent être:

• Équilatéraux, Si ses trois côtés ont la même mesure.
• Isocèle, Lorsque seuls deux des côtés ont une mesure égale, tandis que le troisième est différent.
• Scalène, Si les trois côtés ont une taille différente.

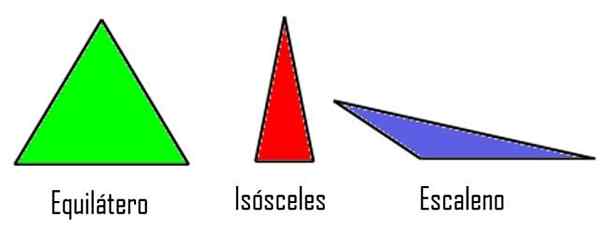Triangles selon leurs côtés. Wikimedia Commons modifiée

Triangles selon ses angles internes

Ce critère est basé sur les types d'angle interne du triangle. Selon cela, un triangle peut être:

• Acutangle, Lorsque les trois angles internes du triangle sont aigus.
• Rectangle, Si le triangle a un angle de mesure interne égal à 90º.
• Obtus, L'un des angles internes du triangle est obtus.

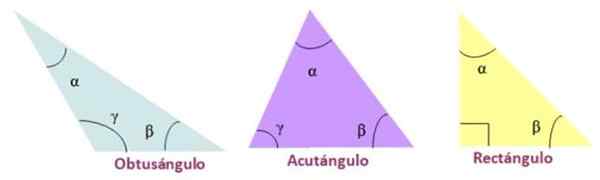Types de triangle selon ses angles internes. Source: F. Zapata

Segments de triangle notables

Parmi les segments notables de tout triangle, ils ont:

• Médian, segment dirigé d'un sommet, directement vers le côté opposé.
• Médiatrice, C'est un segment appartenant à la ligne perpendiculaire au côté, qui se croit au milieu de ce côté.
• Bissecteur, segment qui divise un angle interne en deux parties égales, et qui s'étend au côté opposé à l'angle.
• Hauteur, segment perpendiculaire sur le côté, qui s'étend au sommet opposé.

Peut vous servir: Interpolation de Lagrange

Trois médiums, trois MediaTrices peuvent être tracés et ainsi de suite.

Centres de triangle

Dans tout triangle, les points suivants se distinguent (voir la figure suivante):

• Baricentro G, aussi parfois appelé centroïde du triangle, c'est le point d'intersection des médianes et est toujours intérieur au triangle.
• ORTOCENTER H, point auquel les trois hauteurs se croisent.
• Circoncentro ou, C'est le point d'intersection des médias. Il peut être trouvé à l'extérieur du triangle, si cela est obtus, tandis que, dans le triangle rectangulaire, ou coïncide avec le point médian de l'hypoténuse.
• Au centre, Point d'intersection pour les bissecteurs triangulaires.
• Euler hétéro, droit qui unit le barcentrique, l'orthocentre et le circoncentro, dans tout triangle qui n'est pas équilatéral. Il est toujours accompli que la longueur du segment HG soit le double de celle du segment Go.

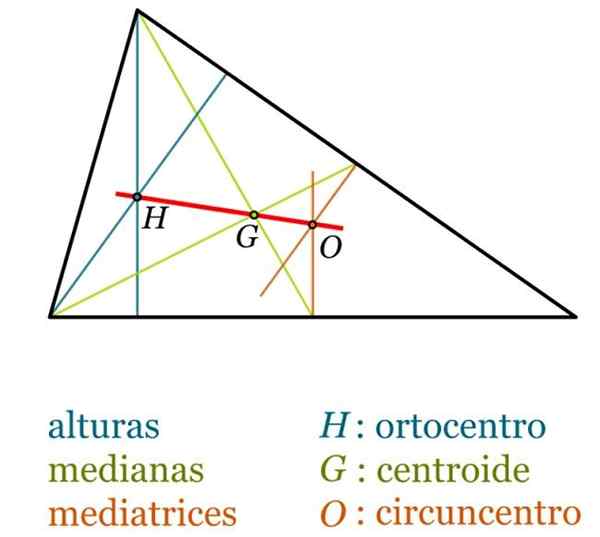Points et segments notables du triangle. Source: Wikimedia Commons

Zone d'un triangle

Pour calculer la zone A du triangle, la formule suivante est utilisée, de nature générale:

A = base × hauteur / 2

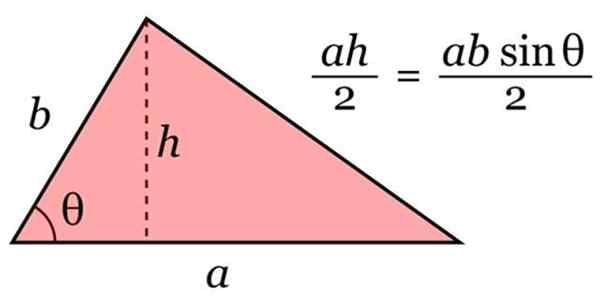Zone du triangle. Source: Wikimedia Commons

Formule Herón

Connaissant la longueur de tous les côtés du triangle, la formule suivante, connue sous le nom Formule Herón, Vous permet de trouver la zone A:

Ici, les côtés du triangle sont a, b et c, tandis que S_p c'est lui semi-périmètre, c'est-à-dire la moitié du périmètre p = a + b + c.

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Angle. Mathematics Libreretsxts. Récupéré de: mathématiques.Bibliothèque.org.
3. Jiménez, René. 2010. Mathématiques II (géométrie et trigonométrie). 2e. Édition. Pearson.
4. Formules d'univers. Triangle. Récupéré de: universoformules.com.
5. Zapata, f. Triangles: histoire, éléments, classification, propriétés. Récupéré de:.com.