Angle enregistré d'une définition de cercle, théorèmes, exemples

Il angle enregistré d'un cercle C'est celui qui a son sommet sur la circonférence et sa semi-sort est sèche ou tangente à la même chose. En conséquence, l'angle enregistré sera toujours convexe ou plat.

Dans la figure 1, plusieurs angles enregistrés dans leurs circonférences respectives sont représentés. L'angle ∠EDF est enregistré en ayant son sommet D sur la circonférence et ses deux semi-recruteurs [de) et [df) sèche la circonférence. 

Figure 1. Plusieurs angles inscrits sur leurs circonférences respectives. Source: F. Zapata avec Geogebra.

De même, l'angle ∠hgi est enregistré, pour avoir son sommet dans la circonférence et ses côtés secs au même.

Les angles ∠kjr et ∠ust sont également enregistrés avec la circonférence. Le premier a un côté sécable et l'autre tangent, tandis que le second a ses deux côtés tangents à la circonférence, formant un angle plan plat (180º).

Certains auteurs appellent un angle semi-inscrit à celui qui a une de ses côtés tangente à la circonférence, mais dans cet article, il est considéré comme enregistré.

Tout angle enregistré définit ou sous-tend un arc associé à. Par exemple, dans la figure 2, l'angle enregistré ∠ABC sous-tend l'arc a⌒c de la longueur d.

La même figure montre l'angle ∠Doe, qui n'est pas enregistré dans la circonférence pour ne pas avoir son sommet sur sa circonférence, mais au centre ou.

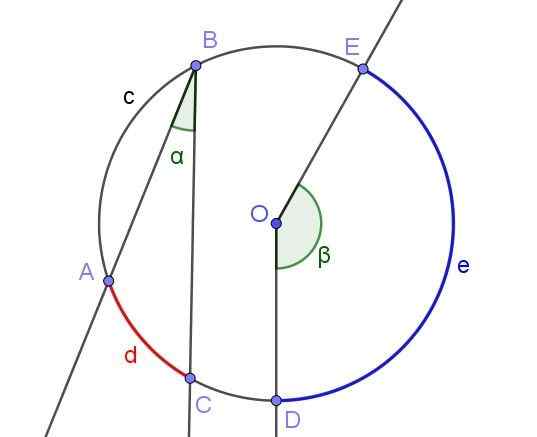Figure 2. Angle enregistré ∠ABC et angle central ∠doe. Source: F. Zapata avec Geogebra.

[TOC]

Angle central

En plus de l'angle enregistré, le angle central, qui est celui dont le sommet est au centre de la circonférence et dont les côtés ont coupé la circonférence.

Peut vous servir: différence entre une fraction commune et un nombre décimal

La mesure des rayons d'un angle central est le quotient entre l'arc qui sous-tend, c'est-à-dire l'arc de circonférence entre les côtés de l'angle et le rayon de la circonférence.

Si la circonférence est unitaire (rayon 1), alors la longueur de l'arc dans les mêmes unités radio est la mesure de l'angle dans les rayons.

Et lorsque la mesure de l'angle est requise en degrés, la mesure est multipliée en radians par le facteur 180º / π.

Les instruments de mesure des angles utilisent toujours un angle central et la longueur de l'arc sous-tendu par ceci directement calibré en degrés. Cela signifie que chaque fois qu'un angle est mesuré, en arrière-plan, ce qui est mesuré est la longueur de l'arc sous-tendu par l'angle central.

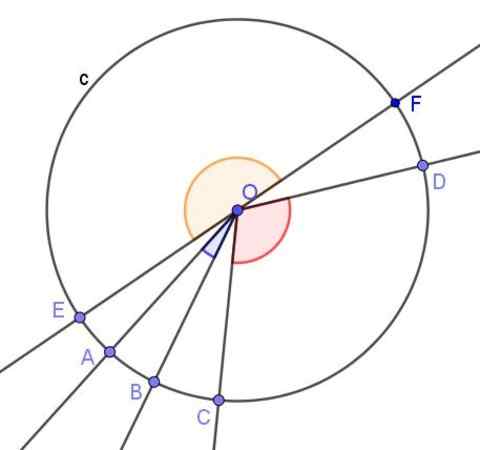figure 3. Plusieurs angles centraux de la circonférence. Source: F. Zapata avec Geogebra.

Théorèmes

- Théorème 1 (angle enregistré et angle central)

La mesure d'un angle enregistré est la moitié de la mesure de l'angle central, si les deux angles sous-disent le même arc.

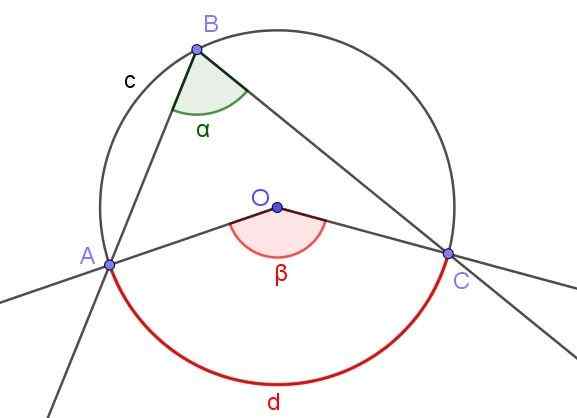Figure 4. Angle enregistré ∠ABC et angle central ∠aoc qui sous-tirite le même arc a⌒c. Source: F. Zapata avec Geogebra.

La figure 4 montre deux angles ∠ABC et ∠AOC, qui coupent le même arc de circonférence a⌒c.

Si la mesure de l'angle enregistré est α, alors la mesure β de l'angle central est le double de la mesure de l'angle enregistré (β = 2 α) car les deux soustraient le même arc mesuré D.

Démonstration 1

Pour démontrer le théorème 1, plusieurs cas particuliers commenceront, jusqu'à atteindre le cas général.

Peut vous servir: Sandwich Loi: Explication et exercices

Supposons un angle enregistré, dans lequel l'un de ses côtés passe à travers le centre de la circonférence, comme le montre la figure 5.

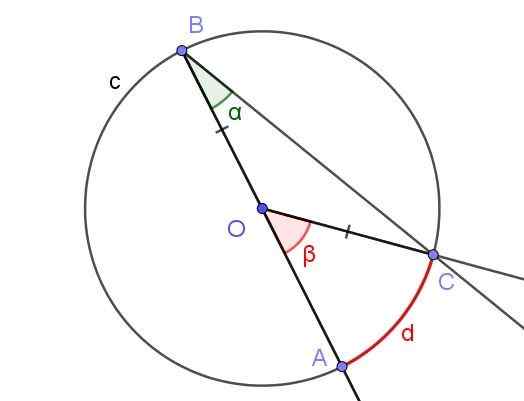Figure 5. Angle enregistré ∠ABC avec le côté [BA) à travers O et Angle central ∠AOC. Source: F. Zapata avec Geogebra.

Dans ce cas, le triangon isocèle COB est formé, puisque [OC] = [OB].

Dans un triangle isocèle, les angles adjacents à la base sont les mêmes, ils doivent donc ∠bco = ∠abc = α. En revanche ∠cob = 180º - β.

Compte tenu de la somme des angles internes du triangle COB que vous avez:

α + α + (180º - β) = 180º

Où il suit que 2 α = β, ou ce qui est équivalent: α = β / 2. Cela coïncide avec ce que le théorème 1 indique: la mesure de l'angle enregistré est la moitié de l'angle central, si les deux angles soumettent la même corde [AC].

Démonstration 1b

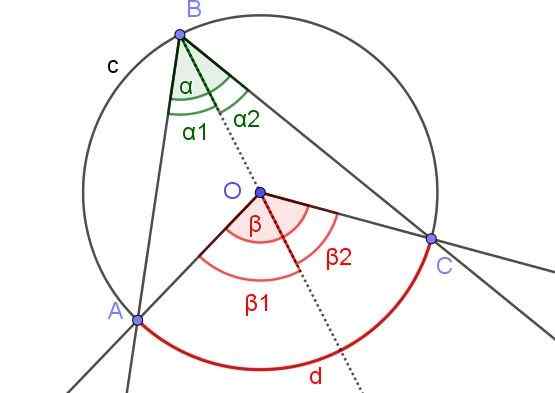Figure 6. Construction auxiliaire pour démontrer que α = β / 2. Source: F. Zapata avec Geogebra.

Dans ce cas, il y a un angle inscrit ∠ABC, dans lequel le centre ou la circonférence est à l'intérieur de l'angle.

Pour démontrer le théorème 1 dans ce cas, l'auxiliaire semi-droit [bo) est dessiné, de sorte qu'il y a deux angles enregistrés ∠abo et ∠OBC adjacent audit semi-recréation.

De même, ils ont les angles centraux β₁ et β₂ adjacent à ladite. De cette façon, vous avez la même situation que dans la démonstration 1, il peut donc être indiqué que α₂ = β₂ / 2 et α₁ = β₁ / 2. Comme α = α₁ + α₂ et β = β₁ + β₂ Il y a donc que α = α₁ + α₂ = β₁ / 2 + β₂ / 2 = (β₁ + β₂) / 2 = β / 2.

Peut vous servir: types d'intégrales

En conclusion α = β / 2, qui rencontre le théorème 1.

- Théorème 2

Si deux angles enregistrés ou plus sous-soient le même arc, alors ils ont la même mesure.

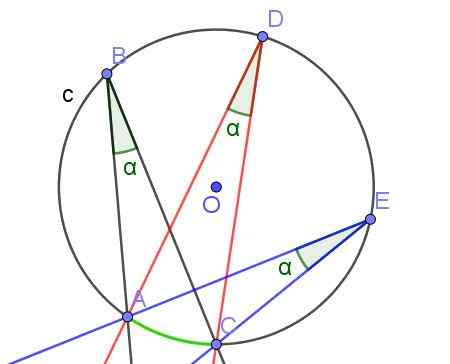Figure 7. Angles enregistrés de mesure égale α, car ils sous -dent le même arc a⌒c. Source: F. Zapata avec Geogebra.

- Théorème 3

Les angles enregistrés sous-tits il y a des chaînes de la même mesure sont les mêmes.

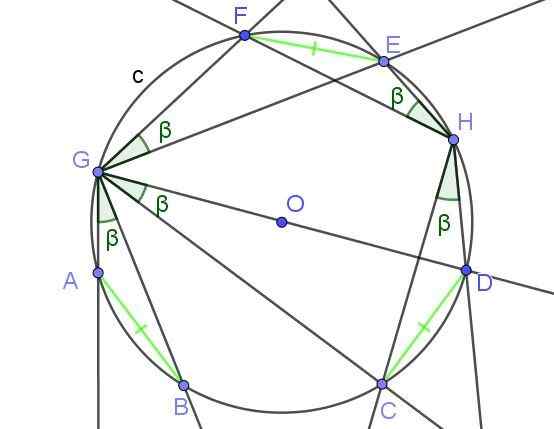Figure 8. Les angles inscrits qui sous-tiennent les cordes de mesure égale, ont une mesure égale β. Source: F. Zapata avec Geogebra.

Exemples

- Exemple 1

Démontrez que l'angle inscrit sous-maîtrise le diamètre est un angle droit.

Solution

L'angle central ∠AOB associé au diamètre est un angle plat, dont la mesure est de 180º.

Selon le théorème 1, tout angle enregistré dans la circonférence qui sous-tend la même corde (dans ce cas le diamètre), a pour mesure la moitié de l'angle central qui sous-tirite la même corde, qui pour notre exemple est 180º / 2 = 90º.

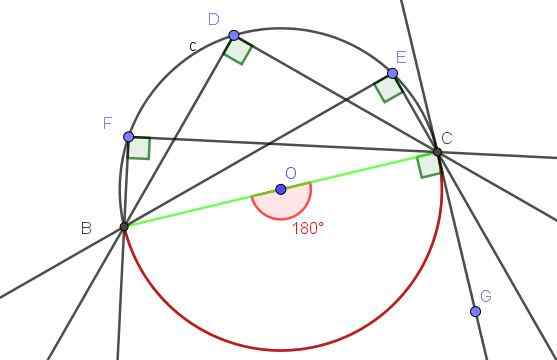Figure 9. Tout angle enregistré qui sous-tend au diamètre est un angle droit. Source: F. Zapata avec Geogebra.

- Exemple 2

La ligne (BC) tangente dans A A A à la circonférence C, détermine l'angle inscrit ∠BAC (voir figure 10).

Vérifiez que le théorème 1 des angles enregistrés est rempli.

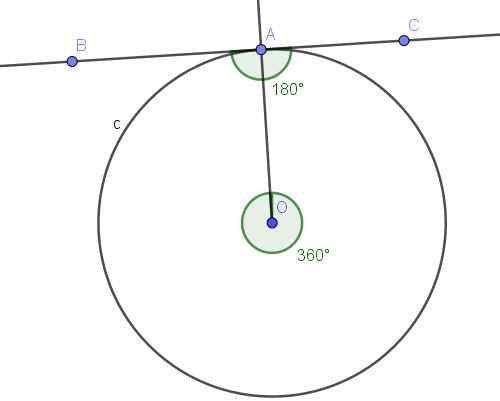Figure 10. Angle enregistré BAC et son angle central convexe AOA. Source: F. Zapata avec Geogebra.

Solution

L'angle ∠bac est enregistré parce que son sommet est sur la circonférence, et ses côtés [AB) et [AC) sont tangents à la circonférence, de sorte que la définition de l'angle inscrit est satisfaite.

D'un autre côté, l'angle inscrit ∠bac sous-tend l'arc A⌒a, qui est la circonférence complète. L'angle central qui sous-tend l'arc A⌒a est un angle convexe dont la mesure est le plein angle (360º).

L'angle enregistré sous-marie, l'arc complet mesure la moitié de l'angle central associé, c'est-à-dire ∠BAC = 360º / 2 = 180º.

Avec tout ce qui précède, il est prouvé que ce cas particulier rencontre le théorème 1.

Les références

1. Baldor. (1973). Géométrie et trigonométrie. Éditorial culturel d'Amérique centrale.
2. ET. POUR. (2003). Éléments de géométrie: avec des exercices et une géométrie de la boussole. Université de Medellin.
3. Géométrie 1ère. Angles dans la circonférence. Récupéré de: edu.Xunta.est/
4. Toute science. Exercices proposés d'angles dans la circonférence. Récupéré de: Francesphysics.Blogspot.com
5. Wikipédia. Angle enregistré. Récupéré de: est.Wikipédia.com