Échantillonnage stratifié ce qui est, types, avantages et inconvénients

Il Échantillonnage stratifié, O Stratification, c'est une méthode d'échantillonnage qui implique la division d'une population en sous-groupes plus petits, appelés strates. À leur tour, ces strates sont formées sur la base des attributs ou des caractéristiques partagées des membres, telles que le revenu ou le niveau éducatif.

Il est utilisé pour mettre en évidence les différences entre les groupes d'une population, contrairement à un échantillonnage simple, qui traite tous les membres d'une population comme des égaux, avec la même probabilité d'être échantillonné.

Source: NeedPix.com

L'objectif est d'améliorer la précision de l'échantillon en réduisant l'erreur d'échantillonnage. Il peut produire une moyenne pondérée avec moins de variabilité que la moyenne arithmétique d'un simple échantillon de la population.

La stratification est le processus de fragmentation avant d'échantillonner les membres d'une population en sous-ensemble homogène. Grâce aux strates, une distribution de population est définie.

C'est-à-dire qu'il doit être collectivement exhaustif et mutuellement exclusif, donc une seule strate doit être affectée à chaque élément de la population. Alors un échantillonnage systématique ou simple est appliqué dans chaque strate.

[TOC]

Considérations importantes

Il est important de noter que les strates ne doivent pas être juxtaposées. Avoir des sous-groupes superposés donnera à certaines personnes plus de possibilité d'être sélectionnées comme sujets. Cela entrave totalement la notion d'échantillonnage stratifié en tant que prototype d'échantillonnage.

Il est tout aussi important que le chercheur utilise un échantillonnage simple dans les différentes strates.

Les couches les plus courantes utilisées dans l'échantillonnage stratifié sont l'âge, le sexe, le niveau socioéconomique, la religion, la nationalité et le niveau d'éducation.

Qu'est-ce que l'échantillonnage stratifié?

Lorsque vous terminez l'analyse dans un groupe d'entités ayant des caractéristiques similaires, un chercheur peut constater que la taille de la population est trop importante pour conclure cette recherche.

Pour économiser du temps et de l'argent, vous pouvez adopter une perspective plus réalisable en sélectionnant un petit groupe de population. Ce petit groupe est appelé la taille de l'échantillon, qui est un sous-ensemble de la population utilisée pour représenter l'ensemble de la population.

Vous pouvez sélectionner un échantillon d'une population de plusieurs manières, dont l'un est avec l'échantillonnage stratifié. Cela implique de diviser la population totale en groupes homogènes appelés strates. Puis des échantillons aléatoires de chaque strate sont sélectionnés.

Processus pour effectuer un échantillonnage stratifié

- Divisez la population en sous-groupes ou strates plus petits, selon les attributs et les caractéristiques partagés par les membres.

- Prenez un échantillon aléatoire de chaque strate dans un nombre proportionnel à la taille de la strate.

- Regrouper le sous-ensemble de strates pour former un échantillon aléatoire.

Peut vous servir: exhort criminel

- Effectuer l'analyse.

Par exemple, considérez un chercheur qui souhaite connaître le nombre d'étudiants en administration qui ont reçu une offre d'emploi dans les trois mois suivant leur diplôme en 2018. Vous découvrirez bientôt qu'il y en avait presque 200.000 diplômés d'administration cette année-là.

Je pourrais décider de prendre simplement un échantillon aléatoire de 5.000 diplômés et réaliser l'enquête. Mieux encore, pourrait diviser la population en strates et prélever un échantillon aléatoire sur ces strates.

Pour ce faire, je créerais des groupes d'âge en fonction de l'âge, de la race, de la nationalité ou de l'histoire professionnelle.

Un échantillon aléatoire de chaque strate serait prélevé, proportionnellement à la taille de la couche par rapport à la population totale. Ces sous-ensembles seraient regroupés pour former un échantillon.

Gars

Échantillonnage stratifié proportionnel

Dans ce type, la taille de l'échantillon pour chaque strate est proportionnelle à la taille de la population de la population par rapport à la population totale. Cela signifie que chaque strate a la même proportion d'échantillonnage.

Lorsqu'une caractéristique des individus est sélectionnée pour définir les strates, les sous-groupes résultants sont souvent de tailles différentes.

Par exemple, nous voulons étudier le pourcentage de la population mexicaine qui fume. Trois couches sont définies:

- Moins de 20 ans.

- Entre 20 et 44.

- Supérieur à 44.

Lorsque la population du Mexique est divisée en ces trois couches, les trois groupes ne devraient pas être de la même taille. En fait, de vraies données le confirment:

- La strate 1: 42.4 millions (41.0%).

- Stratum 2: 37.6 millions (36.3%).

- Stratum 3: 23.5 millions (22.7%).

Si un échantillonnage stratifié proportionnel est utilisé, l'échantillon doit être composé de strates qui maintiennent les mêmes proportions que la population. Si vous souhaitez créer un échantillon de 1.000 personnes, les échantillons doivent avoir les tailles suivantes:

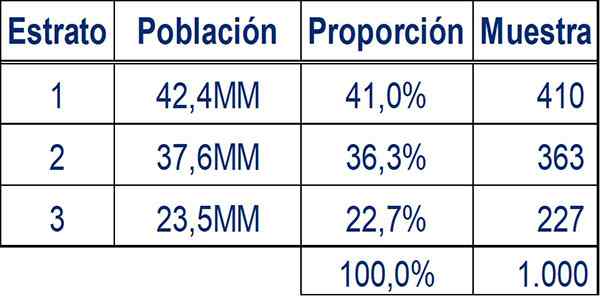
Il est très similaire à la collecte d'une population plus petite, déterminée par les proportions relatives des strates au sein de la population.

Échantillonnage stratifié uniforme

Dans ce type, la même taille d'échantillon est attribuée à toutes les strates définies, quel que soit le poids de ces strates au sein de la population.

Un échantillonnage stratifié uniforme prenant l'exemple précédent produirait l'échantillon suivant pour chaque strate:

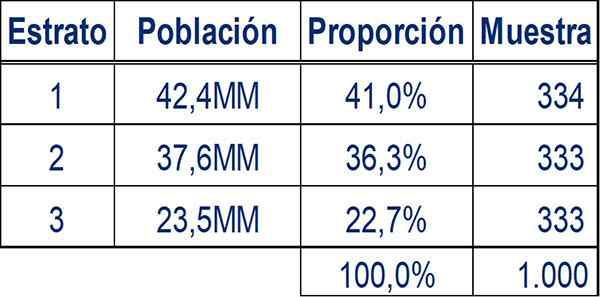
Cette méthode favorise les strates qui ont moins de poids dans la population, en leur accordant le même niveau d'importance que les strates les plus pertinentes.

Il peut vous servir: histoire et évolution de la qualité

Cela réduit l'efficacité globale de l'échantillon, mais permet d'étudier plus de précision les caractéristiques individuelles de chaque strate.

Dans l'exemple, si vous souhaitez faire une déclaration spécifique sur la population de la strate 3 (plus de 44), les erreurs d'échantillonnage pourraient être réduites en utilisant un échantillon de 333 unités, au lieu d'un échantillon de 227 unités, comme obtenu à partir de l'échantillonnage stratifié proportionnel.

Avantages et inconvénients

L'échantillonnage stratifié fonctionne bien pour les populations qui ont une variété d'attributs, mais sinon, il ne sera pas efficace si les sous-groupes ne peuvent pas être formés.

- avantage

Collectez les fonctionnalités clés

Le principal avantage de l'échantillonnage stratifié est que les caractéristiques clés de la population se rassemblent dans l'échantillon.

Semblable à une moyenne pondérée, cette méthode d'échantillonnage produit des caractéristiques de l'échantillon qui sont proportionnelles à la population totale.

Plus grande précision statistique

La stratification donne une erreur plus faible dans l'estimation que la méthode d'échantillonnage simple. Plus la différence entre les strates est grande, plus le profit de précision est grand.

Il y a une plus grande précision statistique lors de la comparaison avec un échantillonnage simple. En effet, au sein des sous-groupes, la variabilité est plus faible, par rapport aux variations présentées avec la population totale.

Taille de l'échantillon plus petit

Comme cette technique a une précision statistique élevée, elle signifie également qu'elle nécessite une taille d'échantillon plus petite, ce qui peut économiser beaucoup d'efforts, de l'argent et du temps des chercheurs.

- Désavantages

Malheureusement, cette méthode de recherche ne peut pas être utilisée dans toutes les études. L'inconvénient de la méthode est que plusieurs conditions doivent être remplies pour être utilisées correctement.

Difficulté à trouver des couches

Le principal inconvénient est qu'il peut être difficile d'identifier les couches appropriées pour une étude. De plus, trouver une liste exhaustive et définitive d'une population entière peut être un défi.

Complexité à organiser

Un deuxième inconvénient est qu'il est plus complexe d'organiser et d'analyser les résultats par rapport à un échantillonnage simple.

Les chercheurs doivent identifier chaque membre d'une population à l'étude et la classer dans une seule sous-population. En conséquence, l'échantillonnage stratifié est désavantageux lorsque les chercheurs ne peuvent pas classer chaque membre de la population en toute confiance dans un sous-groupe.

La juxtaposition peut être un problème s'il y a des sujets divisés en plusieurs sous-groupes. Lorsque l'échantillonnage simple est effectué, ceux qui sont dans plusieurs sous-groupes seront choisis. Le résultat pourrait être une fausse déclaration ou un reflet inexact de la population.

Peut vous servir: Ernest Dale: biographie et contributions à l'administration

Des exemples tels que les étudiants universitaires, les diplômés, les hommes et les femmes, le rendent facile, car ce sont des groupes clairement définis.

Cependant, dans d'autres situations, cela pourrait être beaucoup plus difficile. Vous pouvez imaginer incorporer des caractéristiques telles que la race, l'origine ethnique ou la religion. Le processus de classification deviendrait plus difficile, transformant l'échantillonnage stratifié en une méthode inefficace.

Exemple

Supposons qu'une équipe de recherche souhaite déterminer les notes moyennes des étudiants universitaires aux États-Unis.

L'équipe de recherche a des difficultés évidentes à collecter ces données auprès des 21 millions d'étudiants universitaires. Par conséquent, décide de prélever un échantillon de la population, en utilisant seulement 4.000 étudiants.

L'équipe observe les différents attributs des participants à l'échantillon et se demande en cas de différence entre les notes moyennes et la spécialisation des étudiants.

C'est dans l'échantillon que 560 étudiants sont des étudiants en anglais, 1.135 des sciences, 800 de l'informatique, 1.090 Ingénierie et 415 mathématiques.

L'équipe veut utiliser un échantillonnage stratifié proportionnel, où les strates d'échantillon sont proportionnelles à l'échantillon de population.

Création de strates

Pour ce faire, l'équipe enquête sur les statistiques des étudiants universitaires aux États-Unis.Uu. Et trouvez le pourcentage officiel d'étudiants qui se spécialisent: 12% en anglais, 28% en sciences, 24% en informatique, 21% en ingénierie et 15% en mathématiques.

Par conséquent, cinq strates sont créées à partir du processus d'échantillonnage stratifié. L'équipe doit confirmer que la strate de la population est proportionnelle à la strate d'échantillon. Cependant, il constate que les proportions ne sont pas égales.

Par conséquent, l'équipe doit revenir à un échantillon de la population de 4 personnes.000 étudiants, mais cette fois, sélectionnant au hasard 480 (12%) étudiants en anglais, 1.120 (28%) des sciences, 960 (24%) de l'informatique, 840 (21%) Engineering et 600 (15%) mathématiques.

Avec cela, il existe un échantillon proportionnel stratifié d'étudiants universitaires, qui offre une meilleure représentation des étudiants universitaires aux États-Unis.Uu.

Les chercheurs peuvent mettre en évidence une strate spécifique, observer les différentes études des étudiants de l'Université américaine.Uu. et observer les différentes moyennes des notes.

Les références

1. Adam Hayes (2019). Échantillonnage aléatoire stratifié. Tiré de: Investopedia.com.
2. Wikipedia, The Free Encyclopedia (2019). Échantillonnage stratifié. Pris de: dans.Wikipédia.org.
3. Explorable (2019). Méthode d'échantillon stratifié. Tiré de: explorable.com.
4. Survey Gizmo (2019). Qu'est-ce que l'échantillon stratifié et quand est? Tiré de: Surveygizmo.com.
5. Ashley Crossman (2019). Comprendre les échantillons stratifiés et comment les faire. Pensée co. Tiré de: Thoughtco.com.
6. Carlos Ochoa (2017). Échantillonnage aléatoire: échantillonnage stratifié. Tiré de: NetQuest.com.