Méthodologie d'échantillonnage aléatoire, avantages, inconvénients, exemples

Il échantillonnage aléatoire C'est le moyen de sélectionner un échantillon statistiquement représentatif d'une population donnée. Partie du principe selon lequel chaque élément de l'échantillon doit avoir la même probabilité d'être sélectionné.

Une tombola est un exemple d'échantillonnage aléatoire, dans lequel chaque membre de la population de participants se voit attribuer un nombre. Pour choisir les nombres correspondant aux Raffle Awards (l'échantillon) Une technique aléatoire est utilisée, par exemple extraire d'une boîte aux lettres Les nombres qui ont été notés sur des cartes identiques.

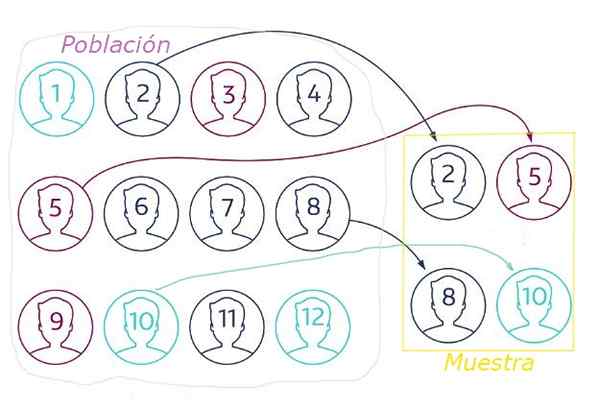Figure 1. Dans l'échantillonnage aléatoire, l'échantillon est extrait de la population aléatoire par une technique qui garantit que tous les éléments ont la même probabilité d'être choisi. Source: NetQuest.com.

Dans l'échantillonnage aléatoire, il est essentiel.

[TOC]

La taille de l'échantillon

Il existe des formules pour déterminer la taille appropriée d'un échantillon. Le facteur le plus important à considérer est de savoir si la taille de la population est connue ou non. Regardons les formules pour déterminer la taille de l'échantillon:

Cas 1: La taille de la population n'est pas connue

Lorsque la taille de la population est inconnue, il est possible de sélectionner un échantillon n adéquat, pour déterminer si une certaine hypothèse est vraie ou fausse.

Pour cela, la formule suivante est utilisée:

n = (z² P q) / (e²)

Où:

-P c'est la probabilité que l'hypothèse est vraie.

-Q est la probabilité qu'il ne soit donc pas, Q = 1 - P.

-E est la marge d'erreur relative, par exemple une erreur de 5% a une marge E = 0,05. 

-Z a à voir avec le niveau de confiance requis par l'étude.

Peut vous servir: distribution normale: formule, caractéristiques, exemple, exercice

Dans une distribution normale caractérisée (ou normalisée), un niveau de confiance à 90% a z = 1 645, car la probabilité que le résultat se situe entre -1 645σ et + 1 645σ est de 90%, où σ est l'écart type.

Niveaux de confiance et leurs valeurs Z correspondantes 

1.- Le niveau de confiance de 50% correspond à z = 0,675.

2.- 68.Le niveau de confiance de 3% correspond à z = 1.

3.- 90% Niveau de confiance équivalent à z = 1 645.

4.- Le niveau de confiance à 95% correspond à z = 1,96

5.- Le niveau de confiance de 95,5% correspond à z = 2.

6.- Le niveau de confiance à 99,7% équivaut à z = 3.

Un exemple dans lequel cette formule peut être appliquée serait dans une étude pour déterminer le poids moyen des cailloux d'une plage.

Il n'est clairement pas possible d'étudier et de peser tous les cailloux de la plage, donc c'est pratique.

Figure 2. Pour étudier les caractéristiques des cailloux d'une plage, il est nécessaire de choisir un échantillon aléatoire avec un nombre représentatif d'entre eux. (Source: Pixabay)

Cas 2: La taille de la population est connue

Lorsque le nombre n des éléments qui composent une certaine population (ou univers) est connu, si vous souhaitez sélectionner par échantillonnage aléatoire simple d'un échantillon d'échantillon statistiquement significatif, c'est la formule: 

n = (z²p q n) / (n e² + Z²P q)

Où:

-Z est le coefficient associé au niveau de confiance.

-P est la probabilité de succès de l'hypothèse.

-Q est la probabilité d'échec dans l'hypothèse, p + q = 1.

-N est la taille de la population totale.

-E est l'erreur relative du résultat de l'étude.

Exemples

La méthodologie pour extraire les échantillons dépend beaucoup du type d'étude nécessaire pour faire. Par conséquent, l'échantillonnage aléatoire a d'innombrables applications:

Peut vous servir: signes de regroupement

Enquêtes et questionnaires

Par exemple dans les enquêtes téléphoniques, les gens sont choisis pour être consultés par un générateur de nombres aléatoires, applicable à la région à l'étude.

Si vous souhaitez appliquer un questionnaire aux employés d'une grande entreprise, la sélection des répondants peut être utilisée par le biais de leur numéro d'employé ou numéro d'identité.

Ce numéro doit également être choisi au hasard, en utilisant un générateur de nombres aléatoires par exemple.

figure 3. Un questionnaire peut être appliqué au hasard en sélectionnant les participants. Source: Pixabay.

Contrôle de qualité

Dans le cas où l'étude est sur les pièces fabriquées par une machine, les pièces doivent être choisies au hasard, mais des lots fabriqués à différents moments de la journée, ou dans différents jours ou semaines.

avantage

Échantillonnage aléatoire simple:

- Il permet de réduire les coûts d'une étude statistique, car il n'est pas nécessaire d'étudier la population totale pour obtenir des résultats statistiquement fiables, avec les niveaux de confiance souhaités et le niveau d'erreur requis dans l'étude.

- Éviter les biais: comme le choix des éléments à étudier est complètement au hasard, l'étude reflète fidèlement les caractéristiques de la population, bien qu'une seule partie de la même chose ait été étudiée.

Désavantages

- La méthode n'est pas adéquate dans les cas que vous souhaitez connaître les préférences dans différents groupes ou strates de population.

Dans ce cas, il est préférable de déterminer précédemment les groupes ou segments sur lesquels l'étude est réalisée. Une fois que les strates ou les groupes ont été définis, alors s'il est pratique pour chacun d'eux d'appliquer un échantillonnage aléatoire.

- Il est très peu probable que des informations sur les secteurs minoritaires soient obtenues, dont il est parfois nécessaire de connaître leurs caractéristiques.

Peut vous servir: règle Simpson: formule, démonstration, exemples, exercices

Par exemple, s'il s'agit d'une campagne sur un produit coûteux, il est nécessaire de connaître les préférences des secteurs minoritaires les plus riches.

Exercice résolu

Nous voulons étudier la préférence de la population par la façon dont Cola de Cola, mais il n'y a pas d'étude antérieure dans cette population, dont sa taille est inconnue.

D'un autre côté, l'échantillon doit être représentatif avec un niveau de confiance minimum de 90% et les conclusions doivent avoir une erreur en pourcentage de 2%.

-Comment déterminer la taille S de l'échantillon?

-Quelle serait la taille de l'échantillon si la marge d'erreur est faite jusqu'à 5%?

Solution

Étant donné que la taille de la population est inconnue, pour déterminer la taille de l'échantillon, la formule donnée ci-dessus est utilisée:

n = (z²P q) / (e²)

Nous supposons qu'il existe la même probabilité de préférence (P) par notre rafraîchissement de celle de la non-préférence (Q), alors p = q = 0,5.

D'un autre côté, comme le résultat de l'étude doit avoir une erreur en pourcentage inférieure à 2%, alors l'erreur relative sera de 0,02.

Enfin, une valeur z = 1 645 produit un niveau de confiance de 90%.

En bref, vous avez les valeurs suivantes:

Z = 1 645

P = 0,5

Q = 0,5

E = 0,02

Avec ces données, la taille minimale de l'échantillon est calculée:

N = (1 645² 0,5 0,5) / (0,02²) = 1691.3

Cela signifie que l'étude avec la marge d'erreur requise et avec le niveau de confiance choisi, doit avoir un échantillon de répondants d'au moins 1692 individus, choisis par un simple échantillon aléatoire.

Si vous passez d'une marge d'erreur de 2% à 5%, la nouvelle taille de l'échantillon est:

N = (1 645² 0,5 0,5) / (0,05²) = 271

Qui est un nombre significativement inférieur d'individus. En conclusion, la taille de l'échantillon est très sensible à la marge souhaitée dans l'étude.

Les références

1. Berenson, M. 1985.Statistiques pour l'administration et l'économie, les concepts et les applications. Éditorial inter-américain.
2. Statistiques. Échantillonnage aléatoire. Tiré de: EncyclopediaEconoma.com.
3. Statistiques. Échantillonnage. Récupéré de: statistiques.Tapis.Uson.mx.
4. Explorable. Échantillonnage aléatoire. Récupéré de: explorable.com.
5. Moore, D. 2005. Statistiques de base appliquées. 2e. Édition.
6. Netquest. Échantillonnage aléatoire. Récupéré de: NetQuest.com.
7. Wikipédia. Échantillon statistique. Récupéré de: dans.Wikipédia.org