Caractéristiques, types et exemples de mouvement rectiligne

Il mouvement rectilinéaire C'est celui dans lequel le mobile se déplace le long d'une ligne droite et passe donc dans une dimension, reçoit donc également le nom de Mouvement unidimensionnel. Cette ligne droite est le trajectoire ou chemin suivi de l'objet qui se déplace. Les voitures voyageant le long de l'avenue de la figure 1 suivent ce type de mouvement.

C'est le modèle de mouvement le plus simple qui peut être imaginé. Les mouvements quotidiens des personnes, des animaux et des choses combinent souvent les transferts en ligne droite avec des mouvements le long des courbes, mais certains observent souvent certains qui sont exclusivement rectilinéaires.

Figure 1. Voitures se déplaçant le long d'une avenue rectiligne. Source: Pixabay.

Voici quelques bons exemples:

- Lorsque vous exécutez une piste rectiligne de 200 mètres.

- Conduire une voiture sur une route droite.

- Laisser tomber un objet librement d'une certaine hauteur.

- Quand une balle est lancée verticalement.

https: // giphy.com / gifs / j5xx3bynaqv06wtoxq

Maintenant, l'objectif de décrire un mouvement est atteint en spécifiant des caractéristiques telles que:

- Position

- Déplacement

- Vitesse

- Accélération

- Temps.

Pour qu'un observateur détecte le mouvement d'un objet, il est nécessaire d'avoir un point de référence (Origin O) et a établi une adresse spécifique dans laquelle se déplacer, qui peut être l'axe X, L'axe et ou tout autre.

Quant à l'objet qui se déplace, cela peut avoir d'innombrables façons. Il n'y a pas de limites à cet égard, mais dans tout ce qui suit, il sera supposé que le mobile est une particule; un objet si petit que ses dimensions ne sont pas pertinentes.

Il est connu que ce n'est pas le cas pour les objets macroscopiques; Cependant, c'est un modèle avec de bons résultats dans la description du mouvement global d'un objet. De cette façon, une particule peut être une voiture, une planète, une personne ou tout autre objet qui se déplace.

Nous allons commencer notre étude sur la cinématique rectiligne avec une approche générale du mouvement, puis des cas particuliers seront étudiés comme ceux déjà nommés.

[TOC]

Caractéristiques générales du mouvement rectiligne

La description suivante est générale et applicable à tout type de mouvement d'une seule dimension. La première chose est de choisir un système de référence. La ligne le long duquel le mouvement se déroule sera l'axe X. Les paramètres du mouvement:

Position

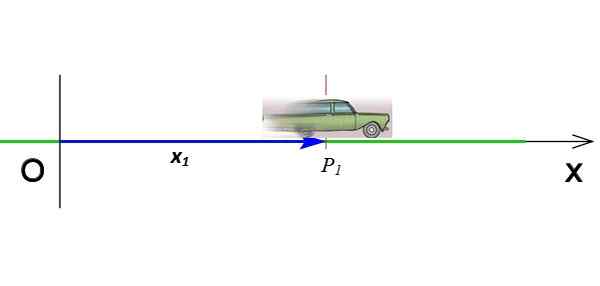Figure 2. Position d'un mobile qui se déplace sur l'axe x. Source: Wikimedia Commons (modifié par F. Zapata).

C'est le vecteur qui passe de l'origine au point où l'objet est en instant donné. Dans la figure 2, le vecteur X₁ Indique la position du mobile lorsqu'elle est dans la coordonnée P₁ Et dans le temps t₁. Les unités vectorielles de position dans le système international sont mètres.

Déplacement

Le déplacement est le vecteur qui indique le changement de position. Dans la figure 3, la voiture est passée de la position P₁ à la position P₂, Par conséquent, son déplacement est δX = X₂ - X₁. Le déplacement est la soustraction de deux vecteurs, il est symbolisé par la lettre grecque Δ ("delta") et est à son tour un vecteur. Ses unités dans le système international sont mètres.

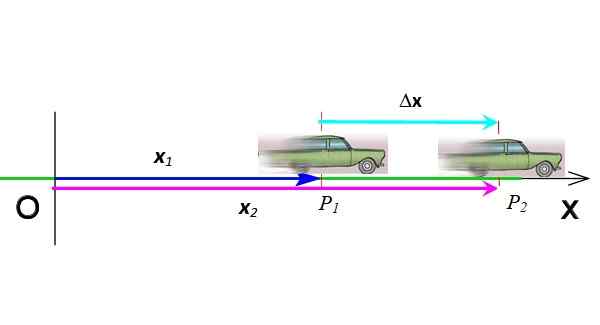figure 3. Déplacement vectoriel. Source: Préparé par F. Zapata.

Les vecteurs sont désignés avec du texte imprimé audacieux. Mais étant sur la même dimension, si vous le souhaitez, vous pouvez vous passer de la notation vectorielle.

Peut vous servir: branches de la physique classique et moderne

Distance parcourue

La distance d Visié par l'objet en mouvement est la valeur absolue du vecteur de déplacement:

D = ΙXΙ = ΔX

Étant une valeur absolue, la distance parcourue est toujours supérieure ou égale à 0 et ses unités sont les mêmes que celles de la position et du déplacement. La notation de valeur absolue peut être effectuée avec des barres de module ou simplement en supprimant la lettre audacieuse dans le texte imprimé.

Vitesse moyenne

À quelle vitesse la position change-t-elle? Il y a des téléphones mobiles lents et rapides. La clé a toujours été la vitesse. Pour analyser ce facteur, la position est analysée X fonction du temps t.

La vitesse moyenne V_m (Voir figure 4) C'est la pente de la ligne de séchage (fuchsia) à la courbe X contre t et fournit des informations mondiales sur le déplacement mobile dans l'intervalle de temps considéré.

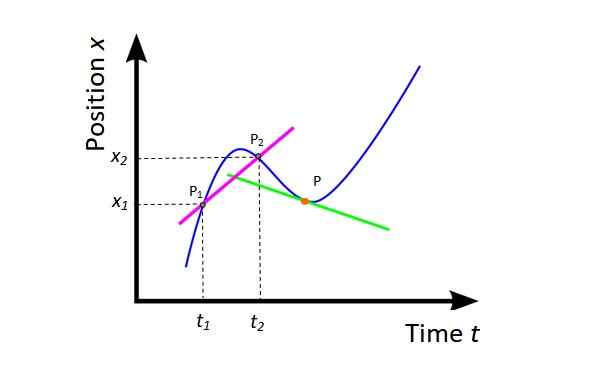Figure 4. Vitesse moyenne et vitesse instantanée. Source: Wikimedia Commons, modifiée par F. Zapata.

V_m = (X₂ - X₁) / (t₂ -t₁) = ΔX / Δt

La vitesse moyenne est un vecteur dont les unités dans le système international sont mètres / seconde (SP).

Vitesse instantanée

La vitesse moyenne est calculée en prenant un intervalle de temps mesurable, mais n'informe pas ce qui se passe dans ledit intervalle. Pour connaître la vitesse à tout moment, vous devez rendre l'intervalle de temps très petit, mathématiquement, il est équivalent à faire:

Δt → 0

L'équation est précédemment donnée pour la vitesse moyenne. De cette façon, la vitesse ou la vitesse instantanée est obtenue:

Géométriquement, la dérivée de la position par rapport au temps est la pente de la ligne tangente à la courbe X contre t à un moment donné. Dans la figure 4, le point est orange et la ligne tangente est verte. La vitesse instantanée à ce stade est la pente de cette ligne.

Vitesse

La vitesse est définie comme la valeur absolue ou le module de vitesse et est toujours positive (la signalisation, les routes et les autoroutes sont toujours positives, jamais négatives). Les termes «vitesse» et «vitesse» peuvent être utilisés quotidiennement, mais en physique, la distinction entre le vecteur et l'escalade est nécessaire.

V = ΙVΙ = V

Accélération moyenne et accélération instantanée

La vitesse peut changer au cours du mouvement et la réalité est qu'il devrait le faire. Il y a une amplitude qui quantifie ce changement: l'accélération. Si nous remarquons que la vitesse est le changement de position par rapport au temps, l'accélération est le changement de vitesse par rapport au temps.

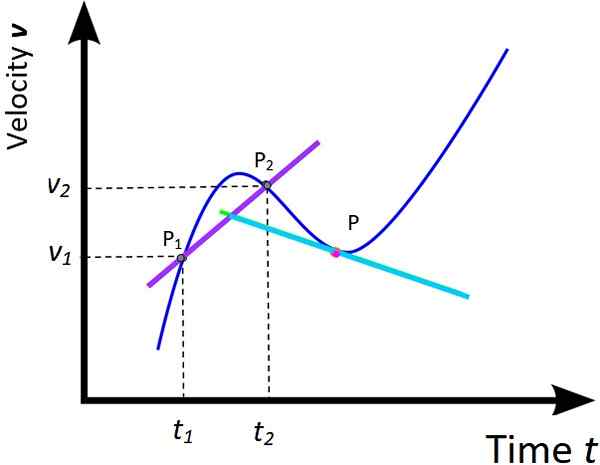Figure 5. Accélération moyenne et accélération instantanée. Source: Wikimedia Commons, modifiée par F. Zapata.

Le traitement donné au graphique de X contre t des deux sections précédentes peuvent être étendues au graphique correspondant de V contre t. Par conséquent, une accélération moyenne et une accélération instantanée sont définies comme suit:

pour_m = (V₂ - V₁) / (t₂ -t₁) = ΔV / Δt  (En attente de la demeure)

Accélération et décélération

Dans le mouvement d'une dimension, les vecteurs par convention ont des signes positifs ou négatifs au fur et à mesure qu'ils vont d'une manière ou d'une autre. Lorsque l'accélération a la même signification que la vitesse, elle augmente son ampleur, mais lorsqu'elle a le sens inverse et que la vitesse diminue son ampleur. On dit alors que le mouvement est retardé.

Peut vous servir: Bouteille Leyden: pièces, opération, expériences

Gars

La classification des mouvements rectilignes est généralement effectuée sur la base de:

- Que l'accélération soit constante ou non.

- Le mouvement passe le long d'une ligne horizontale ou verticale.

Mouvement avec une accélération constante

https: // giphy.com / gifs / ylzfnbidhm7rp391fi

Lorsque l'accélération est constante, l'accélération moyenne pour_m C'est égal à l'accélération instantanée pour Et il y a deux options:

- Que l'accélération vaut 0, auquel cas la vitesse est constante et a un mouvement rectiligne uniforme ou MRU.

- Accélération constante différente de 0, dans laquelle la vitesse augmente ou diminue linéairement dans le temps (le mouvement rectiligne variait uniformément ou MRUV):

Où V_F  et t_F Ils sont respectivement la vitesse finale et le temps, et V_soit et t_soit Ils sont la vitesse et le temps initiaux. Ouais t_soit = 0, Lors de la compensation de la vitesse finale, vous avez l'équation déjà familière pour la vitesse finale:

V_F = V_soit + À

Pour ce mouvement, les équations suivantes sont également valables:

- Position en fonction du temps: x = x_soit + V_{soit .}T + ½ à²

- Vitesse en fonction de la position: V_F² = V_soit² + 2e.ΔX  (Avec Δx = x - x_soit)

Mouvements horizontaux et mouvements verticaux

Les mouvements horizontaux sont ceux qui passent le long de l'axe horizontal ou de l'axe x, tandis que les verticaux le font le long de l'axe et de l'axe. Les mouvements verticaux sous l'action de la gravité sont les plus fréquents et les plus intéressants.

Dans les équations précédentes, il est pris A = g = 9.8 m / s² dirigé verticalement en bas, direction qui est presque toujours choisie avec un signe négatif.

De cette manière, V_F = V_soit + À Il se transforme en V_F = V_soit - GT Et si la vitesse initiale est 0 parce que l'objet a été abandonné librement, il est encore simplifié de V_F = - GT. Tant que la résistance à l'air n'est pas prise en compte, bien sûr.

Exemples résolus

Exemple 1

Au point A, un petit paquet est libéré de sorte qu'il se déplace le long du transporteur avec des roues coulissantes ABCD illustrée sur la figure. Tout en descendant à travers les sections inclinées AB et CD, le package comporte une accélération de 4,8 m / s², tandis que dans la section horizontale, BC maintient une vitesse constante.

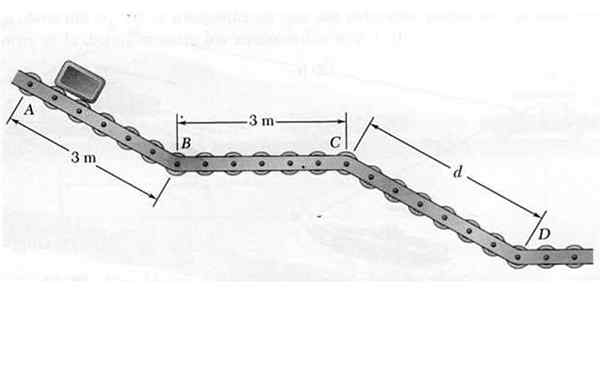Figure 6. L'ensemble qui se déplace sur le chemin coulissant de l'exemple résolu 1. Source: auto-faite.

Sachant que la vitesse à laquelle l'emballage en D est atteint est de 7,2 m / s, déterminez:

a) La distance entre C et D.

b) Le temps requis pour que le package atteigne la fin.

Solution

Le mouvement de l'emballage est effectué dans les trois sections rectilignes indiquées et pour calculer la demande demandée, la vitesse est requise aux points B, C et D. Analysons chaque section séparément:

Section AB

Étant donné que le temps n'est pas disponible dans cette section, il sera utilisé V_F² = V_soit² + 2e.ΔX  Avec vo = 0:

V_F² = 2A.Δx → V_F²= 2. 4,8 m / s² . 3 m = 28.8 m²/² → V_F  = 5.37 m / s = V_B

Le temps que le forfait prend pour parcourir la section AB est:

t_{UN B} = (V_F - V_soit) / A = 5.37 m / s / 4,8 m / s² = 1.19 s

Section BC

La vitesse dans la section BC est constante, donc V_B = V_C = 5.37 m / s. Le temps nécessaire au package pour parcourir cette section est:

Peut vous servir: Réfraction légère: éléments, lois et expérience

t_{avant JC} = distance _{avant JC}  / V_B = 3 m / 5.37 m / s = 0.56 s

Section CD

La vitesse initiale de cette section est V_C = 5.37 m / s, La vitesse finale est V_D = 7,2 m / s, via V_D²  = V_C² + 2. pour. d La valeur de d:

D = (V_D²  - V_C²) / 2.a = (7.2²  - 5.37²) / 2 X 4.8 m = 2.4 m

Le temps est calculé comme:

t_{CD =} (V_D  - V_C) / A = (7.2- 5.37) / 4.8 s = 0.38 s.

Les réponses aux questions soulevées sont:

a) d = 2.4 m

b) le temps de trajet est t_{UN B} + t_{avant JC} + t_CD = 1.19 S +0.56 S +0.38 S = 2.13 s.

Exemple 2

Une personne est sous une porte horizontale qui est initialement ouverte et de 12 m de haut. La personne lance verticalement un objet vers la porte avec une vitesse de 15 m / s.

On sait que la porte se ferme 1,5 seconde après que la personne a lancé l'objet à partir d'une hauteur de 2 mètres. La résistance à l'air ne sera pas prise en compte. Répondez aux questions suivantes, justifiant:

a) parvenez-vous à passer l'objet à travers la porte avant sa fermeture?

b) l'objet entrera-t-il jamais contre la porte fermée? Si affirmatif, quand cela se produit?

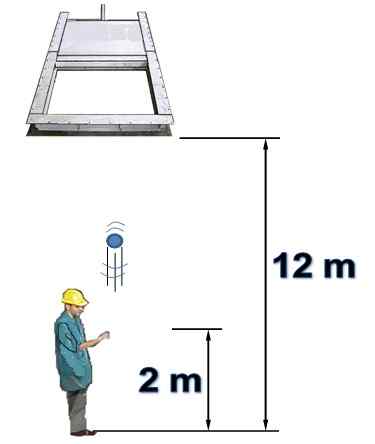Figure 7. Un objet est lancé verticalement (exemple résolu 2). Source: auto-faite.

Réponds à)

Il y a 10 mètres entre la position initiale de la balle et la porte. C'est un lancement vertical, dans lequel cette adresse est considérée comme positive.

Vous pouvez découvrir la vitesse qu'il transporte à votre arrivée à ce stade, avec ce résultat le temps qu'il faudrait pour le faire et le comparer à l'heure de clôture de la porte, qui est 1.5 secondes:

V_F ²= V_soit ²- 2.g. Δet → V_F = (15² - 2 X 9.8 Xdix)^1/2 m = 5.39 m / s

T = (v_F - V_soit) / g = (5.39 - 15) / (-9.8) S = 0.98 s

Comme cette fois est inférieur à 1.5 secondes, puis il est conclu que l'objet peut passer par la porte au moins une fois.

Réponse b)

Nous savons déjà que l'objet gère. La vitesse, quand elle atteint la hauteur de la porte, a la même ampleur que lorsqu'elle monte, mais dans la direction opposée. Travaillez donc avec -5.39 m / s et le temps nécessaire pour atteindre cette situation est:

T = (v_F - V_soit) / G = (-5.39 - 15) / (-9.8) S = 2.08 s

Comme la porte reste ouverte uniquement pour 1.5 s, il est évident qu'il n'a pas le temps de passer avant sa fermeture, car il le trouve fermé. La réponse est: l'objet s'il collite avec la porte fermée après 2.08 secondes après avoir été libérée, quand il est venu en descente.

Les références

1. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Édité par Douglas Figueroa (USB).69-116.
2. Giancoli, D. La physique. (2006). Principes avec les applications. 6^e Édition. Prentice Hall. 22-25.
3. Kirkpatrick, L. 2007. Physique: un regard sur le monde. 6^faire Édition abrégée. Cengage Learning. 23 - 27.
4. Resnick, r. (1999). Physique. Volume 1. Troisième édition en espagnol. Mexique. Société de rédaction continentale S.POUR. de c.V. 21-22.
5. Rex, un. (2011). Fondamentaux de la physique. Pearson. 33 - 36
6. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14^e. Élégant. Volume 1. 50 - 53.
7. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7^mame. Édition. Mexique. Cengage Learning Editors. 23-25.
8. SERAY, R., Vulle, c. (2011). Fondamentaux de la physique. 9^{n / A} Élégant. Cengage Learning. 43 - 55.
9. Wilson, J. (2011). Physique 10. Pearson Education. 133 - 149.