Moment d'inertie formules, équations et exemples de calcul

Il moment d'inertie À partir d'un corps rigide par rapport à un certain axe de rotation, il représente sa résistance à la modification de sa vitesse angulaire autour de cet axe. Il est proportionnel à la masse et aussi à l'emplacement de l'axe de rotation, car le corps, selon sa géométrie, peut plus facilement tourner autour de certains axes que dans d'autres.

Supposons un objet étendu (composé de nombreuses particules) qui peuvent tourner autour d'un axe. Supposons qu'une force agit F, appliqué tangentiellement à l'élément de masse Δm_Toi, qui produit un couple ou un moment, donné par τ_filet = ∑r_Toi X F_Toi. Le vecteur r_Toi C'est la position de Δm_Toi (Voir figure 2).

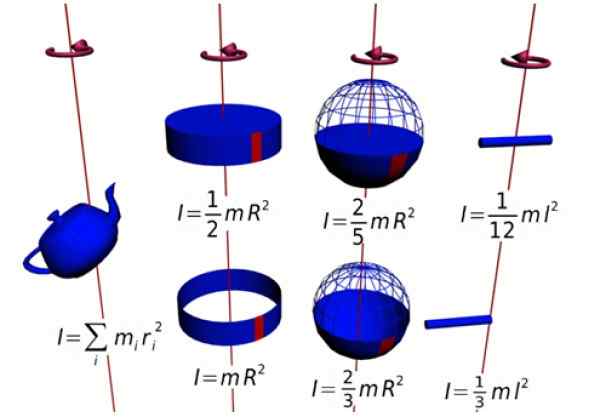
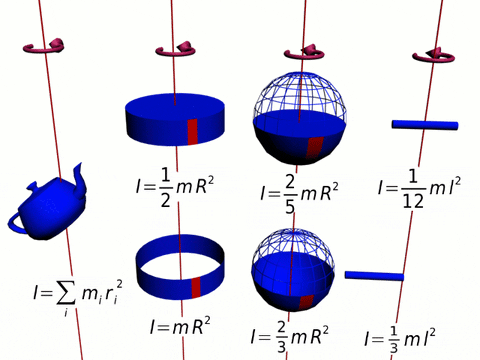Figure 1. Moments d'inertie de plusieurs chiffres. Source: Wikimedia Commons.

Ce moment est perpendiculaire au plan de rotation (adresse +K = Papier en quittant). Étant donné que la résistance et la position radiale sont toujours perpendiculaires, le produit croisé reste:

τ_filet = ∑ f_Toi r_Toi k = ∑ (Δm_Toi pour_Toi) r_Toi  k = ∑ Δm_Toi (pour_Toi r_Toi ) k

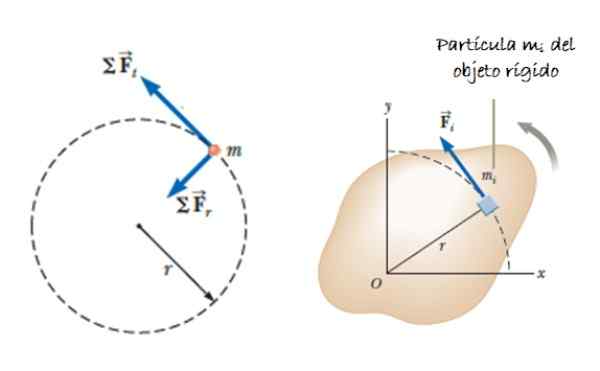Figure 2. Une particule appartenant à un solide rigide en rotation. Source: Serow, R. 2018. Physique pour la science et l'ingénierie. Volume 1. Cengage Learning.

Accélération a_Toi représente la composante tangentielle de l'accélération, car l'accélération radiale ne contribue pas au couple. Selon l'accélération angulaire α, nous pouvons indiquer que:

pour_Toi = α r_Toi

Par conséquent, le couple net est comme ceci:

τ_filet = ∑ Δm_Toi (α r_Toi²) K = (∑ r_Toi² Δm_Toi) α k

Accélération angulaire α est la même pour l'ensemble de l'objet, donc elle n'est pas affectée par l'indice "i" et peut quitter la somme, qui est précisément le moment d'inertie de l'objet symbolisé avec la lettre I:

I = ∑ r_Toi² Δm_Toi

C'est le moment de l'inertie d'une distribution de masse discrète. Lorsque la distribution est continue, la somme est remplacée par une intégrale et Δm devient un différentiel de masse DM. L'intégrale est faite par-dessus tout l'objet:

I = ∫_M(r²) DM

Les unités du moment de l'inertie dans le système international s'ils sont kg x m². C'est un scalaire et une quantité positive, car c'est le produit d'une pâte par le carré d'une distance.

[TOC]

Exemples de calcul

Un objet étendu, comme une barre, un disque, une sphère ou une autre, dont la densité ρ Il est constant et sachant que la densité est le quotient de volume de masse, le différentiel de masse DM Il est écrit comme:

ρ = dm / dv → dm = ρDv

Remplacement dans l'intégrale pour le moment de l'inertie, nous avons:

I = ∫r² ρdv = ρ ∫r²Dv

Il s'agit d'une expression générale, valide pour un objet à trois dimensions, dont le volume V et positionner r Ce sont des fonctions de coordonnées spatiales X, et et z. Notez qu'étant constant, la densité est hors de l'intégrale.

La densité ρ Il est également connu sous le nom de densité volumétrique, mais si l'objet est très plat, comme une feuille ou très mince et étroite comme une tige, d'autres formes de densité peuvent être utilisées, voyons: voyons:

Peut vous servir: mouvement de rotation de la Terre

- Pour une feuille très fine, la densité à utiliser est σ, la densité de surface (masse par unité de zone) et donner est le différentiel de zone.

- Et s'il s'agit d'une barre mince, où seule la longueur est pertinente, la densité de masse linéaire est utilisée λ et un différentiel de longueur, selon l'axe utilisé comme référence.

Dans les exemples suivants, tous les objets sont considérés comme rigides (non reformables) et ont une densité uniforme.

Moment d'inertie d'une barre mince par rapport à un axe qui passe par son centre

Ici, nous allons calculer le moment d'inertie d'une barre mince, rigide et homogène, de longueur L et de masse M, par rapport à un axe qui passe par les moyens.

En premier lieu, il est nécessaire d'établir un système de coordonnées et de construire une figure avec une géométrie adéquate, comme celle-ci:

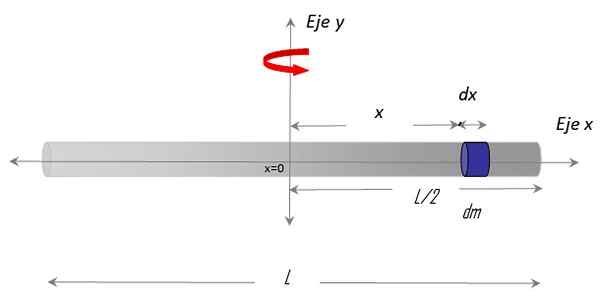figure 3. Géométrie pour calculer le moment d'inertie d'une tige mince par rapport à un axe vertical qui passe par son centre. Source: F. Zapata.

Il a été choisi Axe x le long du bar et le Axe y comme axe de rotation. La procédure pour établir une intégrale nécessite également de choisir un différentiel massique sur la barre, appelé DM, qui a une longueur différentielle Dx et est situé dans la position X arbitraire, en ce qui concerne le centre x = 0.

Selon la définition de la densité de masse linéaire λ:

λ = m / l

Lorsque la densité est uniforme, qui est valable pour M et L, elle est également pour DM et DX:

λ = dm / dx → dm = λdx.

D'un autre côté, l'élément de masse est en position X, Ensuite, en remplaçant cette géométrie dans la définition, nous avons une intégrale définie, dont les limites sont les extrêmes de la barre selon le système de coordonnées:

Remplacement de la densité linéaire λ = m / l:

Pour trouver le moment d'inertie de la barre par rapport à un autre axe de rotation, par exemple celui qui passe par l'un de ses extrémités, vous pouvez utiliser le théorème de Steiner (voir l'exercice résolu à la fin) ou effectuer un calcul direct similaire à celui montré ici, mais modifiant correctement la géométrie.

Moment d'inertie d'un album par rapport à un axe qui passe par son centre

Un album très mince, d'épaisseur méprisable est une figure plate. Si la pâte est uniformément distribuée dans la zone A, la densité de masse σ est:

σ = M / a

Tellement DM comme donner correspondent à la masse et à la zone de l'anneau différentiel indiqué sur la figure. Nous supposerons que l'ensemble entier tourne autour de l'axe et.

Vous pouvez imaginer que l'album est composé que de nombreux anneaux radio concentriques r, chacun avec son moment respectif d'inertie. Ajout des contributions de tous les anneaux jusqu'à ce que vous atteigniez la radio R, Vous aurez l'inertie totale de l'album.

σ = dm / da → dm = σdonner

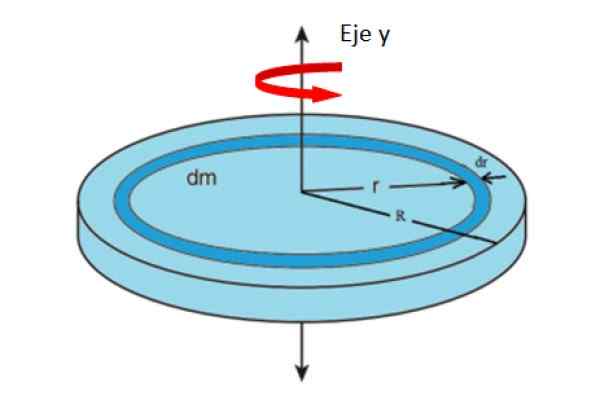Figure 4. Géométrie pour calculer le moment d'inertie d'un album, par rapport à l'axe axial. Source: F. Zapata.

Où m représente toute la pâte de l'album. La zone d'un album dépend de son rayon r comme:

Peut vous servir: vitesse de propagation d'une vague

A = π.r²

Dériver environ r:

Da / dr = 2 = 2π.R → da = 2π.RDR

Remplacement ce qui précède dans la définition de i:

Après avoir évalué les résultats intégraux:

Remplacement σ = m / (π.R² ) est laissé:

Moment d'inertie d'une sphère solide par rapport à un diamètre

Une sphère Radius R peut être considérée comme une série de disques empilés les uns sur les autres, où chaque album de masse infinitésimal DM, radio r et épaisseur Dz, Il a un moment d'inertie donné par:

a donné_disque = (½) R²DM

Pour trouver ce différentiel, la formule de la section précédente a été simplement prise et remplacée M et R pour DM et r, respectivement. Un album comme celui-ci peut être vu dans la géométrie de la figure 5.

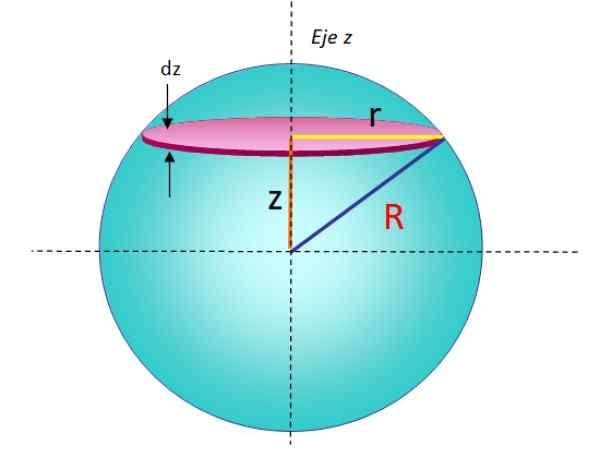Figure 5. Géométrie pour calculer le moment d'inertie d'une sphère de rayon solide par rapport à un axe qui passe à travers un diamètre. Source: F. Zapata.

En ajoutant tous les moments d'inertie infinitésimale des disques empilés, le moment d'inertie totale de la sphère est obtenu:

Toi_sphère = ∫di_disque

Ce qui équivaut à:

I = ∫_sphère (½) R²DM

Pour résoudre l'intégrale, vous devez exprimer DM correctement. Comme toujours, il est réalisé à partir de la densité:

ρ = m / v = dm / dv → dm = ρ.Dv

Le volume d'un disque différentiel est:

Dv = zone de base x hauteur

La hauteur de l'album est l'épaisseur Dz, Alors que la zone de base est πr², donc:

Dv = πr²Dz

Et le remplacement de celui intégré serait comme ceci:

I = ∫_sphère(½) R²Dm = ∫ (½) R²(ρπr²Dz)

Mais avant de l'intégrer, il doit. À travers le théorème de Pythagore:

R² = r² + z² → R² = R² - z²

 Cela nous amène à:

I = ∫_sphère(½) ρ r²(πr²dz) = ∫_sphère(½) ρ π r⁴Dz= ∫_sphère(½) ρ π (r² - z²)² Dz

Pour intégrer toute la sphère, nous remarquons que Z varie entre -R et R, par conséquent:

Sachant que ρ = m / v = m / [(4/3) πr³]] Enfin, il est obtenu, après avoir simplifié:

Moment d'inertie d'un cylindre solide par rapport à l'axe axial

Pour cet objet, une méthode similaire à celle utilisée pour la sphère est utilisée, mais cette fois, il est plus facile si le cylindre est imaginé pour les coquilles radio-cylindriques r, épaisseur Docteur et la hauteur H, Comme s'ils étaient les couches d'un oignon.

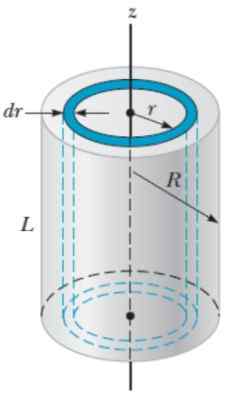Figure 6. Géométrie pour calculer le moment d'inertie d'un cylindre de rayon solide R Respect de l'axe axial. Source: Serow, R. 2018. Physique pour la science et l'ingénierie. Volume 1. Cengage.

Le volume Dv d'une couche cylindrique est:

Dv = 2π.Rl.Docteur

Par conséquent, la masse en cascaron est:

Peut vous servir: échelle microscopique: propriétés, comptes de particules, exemples

Dm = ρ.Dv = ρ. 2π.r.L.Docteur

Cette expression est remplacée dans la définition du moment d'inertie:

 Car ρ = m / (π.R²L) est laissé:

L'équation précédente indique que le moment d'inertie du cylindre ne dépend pas de sa longueur, mais de sa masse et de son rayon uniquement. Ouais L changé, le moment d'inertie par rapport à l'axe axial continuerait d'être le même. Pour cette raison, Toi du cylindre coïncide avec celui de l'album mince précédemment calculé.

Moment d'inertie d'une feuille rectangulaire par rapport à un axe qui passe par son centre

Le Axe y Horizontal comme un axe de rotation. La figure ci-dessous montre la géométrie nécessaire pour effectuer l'intégration:

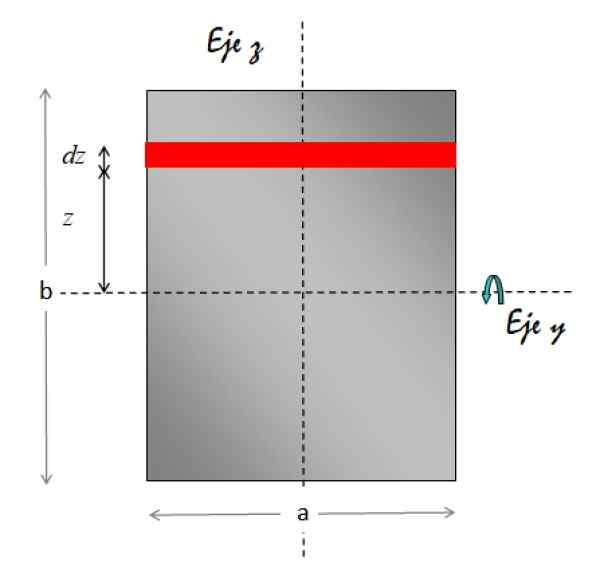Figure 7. Géométrie pour le calcul du moment d'inertie d'une plaque rectangulaire par rapport à un axe parallèle à la feuille et qui passe par son centre. Source: F. Zapata.

L'élément de zone indiqué en rouge est rectangulaire. Sa zone est donc de base x de hauteur:

da = a.Dz

Par conséquent, le différentiel de masse est:

Dm = σ.da = σ.(pour.Dz)

Quant à la distance de l'élément de zone à l'axe de rotation, c'est toujours z. Nous remplaçons tout cela dans l'intégrale du moment de l'inertie:

Maintenant, la densité de masse de surface σ est remplacée par:

σ = m / ab

Et c'est vraiment comme ça:

Notez que c'est comme celui de la barre mince.

Moment d'inertie d'une feuille carrée par rapport à un axe qui passe par son centre

Pour un carré sur le côté L, Dans l'expression précédente valide pour un rectangle, la valeur de b par l'un L:

Théorèmes du moment de l'inertie

Il existe deux théorèmes particulièrement utiles pour simplifier le calcul des moments d'inertie par rapport à d'autres axes, qui pourraient autrement être compliqués à trouver pour le manque de symétrie. Ces théorèmes sont:

Théorème de Steiner

Aussi appelé Théorème de l'axe parallèle, Relate le moment d'inertie concernant un axe avec un autre qui passe par le centre de masse de l'objet, tant que les axes sont parallèles. Pour l'appliquer, la distance d doit être connue entre les deux axes et bien sûr la masse m de l'objet.

Être Toi_z le moment d'inertie d'un objet étendu par rapport à Z, i axe_Cm Le moment de l'inertie par rapport à un axe qui passe par le centre de masse (CM) de cet objet, puis il est accompli que:

Toi_z = I_Cm + MARYLAND²

Ou dans la notation de la figure suivante: Toi_{z '} = I_z + MARYLAND²

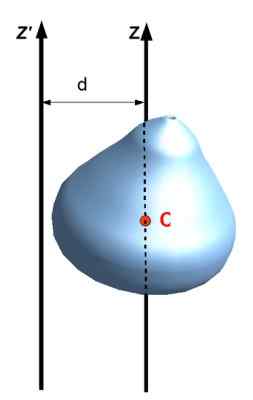Figure 8. Théorème de Steiner ou axes parallèles. Source: Wikimedia Commons. Jack See [CC BY-SA (https: // CreativeCommons.Org / licences / by-sa / 3.0)]

Théorème de l'axe perpendiculaire

Ce théorème s'applique aux surfaces plates et dit: Le moment d'inertie d'un objet plat autour d'un axe perpendiculaire est la somme des moments d'inertie autour de deux axes perpendiculaires au premier axe:

Toi_z = I_X + Toi_et

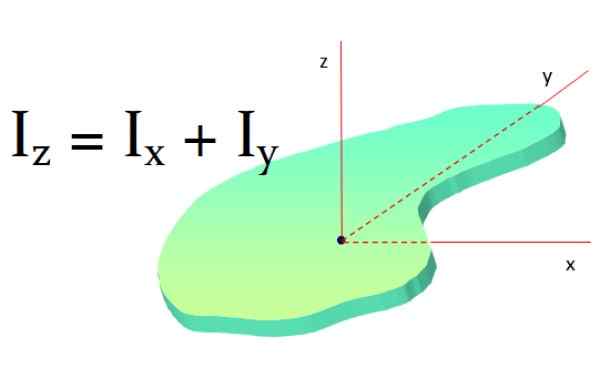Figure 9. Théorème de l'axe perpendiculaire. Source: F. Zapata.

Si l'objet a une symétrie telle que Toi_X et Toi_et Ils sont les mêmes, alors il est accompli que:

Toi_z = 2i_X

Exercice résolu

Trouvez le moment d'inertie de la barre par rapport à un axe qui passe par l'une de ses extrémités, comme celle illustrée à la figure 1 (ci-dessous et à droite) et la figure 10.

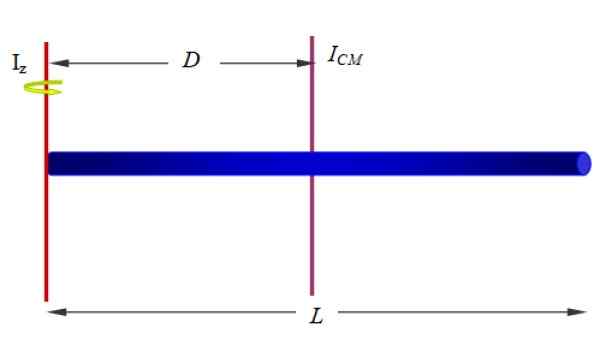Figure 10. Moment d'inertie d'une barre homogène autour d'un axe qui passe à une extrémité. Source: F. Zapata.

Solution:

Nous avons déjà le moment d'inertie de la barre autour d'un axe qui traverse son centre géométrique. Puisque le bar est homogène, son centre de masse est à ce moment-là, donc ce sera le nôtre Toi_Cm Pour appliquer le théorème de Steiner.

Si la longueur de la barre est L, L'axe z est à une distance d = l / 2, donc:

Toi_z = I_Cm + MARYLAND²= (1/12) ml²+M (l / 2)²= (1/3) ml²

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill. 313-340
2. Rex, un. 2011. Fondamentaux de la physique. Pearson. 190-200.
3. Théorème de l'axe parallèle. Récupéré de: hyperphysique.Phy-asch.GSU.Édu.
4. SERAY, R. 2018. Physique pour la science et l'ingénierie. Volume 1. Cengage.
5. Université de Séville. Moment d'inertie des solides sphériques. Récupéré de: Laplace.nous.est.
6. Université de Séville. Moment d'inertie d'un système de particules. Récupéré de: Laplace.nous.est.
7. Wikipédia. Théorème de l'axe parallèle. Récupéré de: dans.Wikipédia.org