Calcul de la matrice inverse et exercice résolu
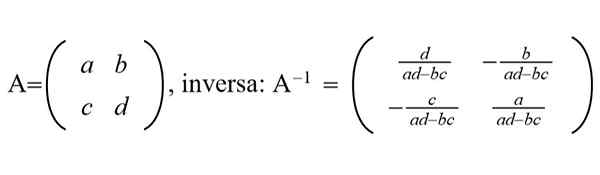
- 1303
- 132
- Raphaël Charles
La Matrice inverse d'une matrice donnée, c'est la matrice qui s'est multipliée par les résultats originaux dans la matrice d'identité. La matrice inverse est utile pour résoudre des systèmes d'équations linéaires, d'où l'importance de savoir comment le calculer.
Les matrices sont très utiles en physique, en ingénierie et en mathématiques, car ils sont un outil compact pour résoudre des problèmes complexes. L'utilité des matrices est améliorée lorsqu'elles sont inversibles et que leur inverse est connu.
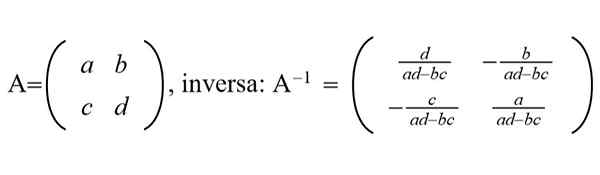 Figure 1. Une matrice générique 2 × 2 et sa matrice inverse sont affichées. (Préparé par Ricardo Pérez)
Figure 1. Une matrice générique 2 × 2 et sa matrice inverse sont affichées. (Préparé par Ricardo Pérez) Dans les champs de traitement graphique, les mégadonnées, l'exploration de données, l'apprentissage automatique et d'autres sont utilisés des algorithmes efficaces et rapides pour évaluer la matrice inverse des matrices NXN avec n très grand, dans l'ordre des milliers ou des millions.
Pour illustrer l'utilisation de la matrice inverse dans la gestion du système d'équations linéaires, nous commencerons par le cas le plus simple de toutes: les matrices 1 × 1.
Le cas le plus simple: une équation linéaire d'une seule variable est considérée: 2 x = 10.
L'idée est de trouver la valeur de x, mais ce sera "matriciel" ".
La matrice M = (2) qui multiplie le vecteur (x) est une matrice 1 × 1 qui entraîne le vecteur (10):
M (x) = (10)
L'inverse de la matrice m est indiqué par m-1.
La façon générale d'écrire ce "système linéaire" est:
M x = b, où x est le vecteur (x) et b est le vecteur (10).
Par définition, la matrice inverse est celle qui s'est multipliée par la matrice d'origine des résultats dans la matrice d'identité I:
M-1 M = I
Dans le cas considéré, la matrice M-1 C'est la matrice (½), c'est-à-dire m-1 = (½) depuis m-1 M = (½) (2) = (1) = i
Peut vous servir: 90 diviseurs: quelles sont et explicationsPour trouver le vecteur inconnu x = (x), dans l'équation surélevée, les deux membres sont multipliés par la matrice inverse:
M-1 M (x) = m-1 (dix)
(½) (2) (x) = (½) (10)
(½ 2) (x) = (½ 10)
(1) (x) = (5)
(x) = (5)
L'égalité de deux vecteurs a été atteinte, qui ne sont les mêmes que lorsque leurs éléments correspondants sont égaux, c'est-à-dire x = 5.
Calcul de l'inverse d'une matrice
Ce qui motive le calcul de la matrice inverse, c'est de trouver une méthode universelle pour la solution de systèmes linéaires tels que le système 2 × 2 suivant:
x - 2 y = 3
-x + y = -2
Après les étapes du cas 1 × 1, étudiées dans la section précédente, nous écrivons le système d'équations de manière matricielle:
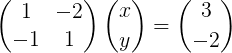 Figure 2. Système linéaire sous forme de matrice.
Figure 2. Système linéaire sous forme de matrice. Notez que ce système est écrit en notation vectorielle compacte comme suit:
M x = b
où
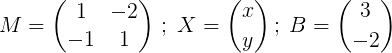
L'étape suivante consiste à trouver m.
Méthode 1: grâce à l'élimination gaussienne
La méthode d'élimination de Gauss sera appliquée. Qui consiste à faire des opérations élémentaires dans les rangs de la matrice, ces opérations sont:
- Multiplier une ligne par un numéro non nul.
- Ajouter ou soustraire une autre ligne, ou le multiple d'une autre ligne.
- Échange de lignes.
L'objectif est, à travers ces opérations, de convertir la matrice d'origine en matrice d'identité.
Comme cela est fait, dans la matrice M exactement les mêmes opérations à la matrice d'identité sont appliquées. Quand après plusieurs opérations dans les lignes R, elle est transformée en matrice unitaire, alors celui qui était à l'origine l'unitaire sera transformé en matrice inverse de m, c'est-à-dire M-1.
Peut vous servir: corollaire (géométrie)1- Nous commençons le processus en écrivant la matrice M et à côté de lui la matrice de l'unité:
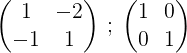
2- Nous ajoutons les deux lignes et le résultat est mis dans la deuxième ligne, de cette façon, nous obtenons un zéro dans le premier élément de la deuxième ligne:
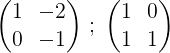
3- Nous multiplions la deuxième ligne par -1 pour obtenir 0 et 1 dans la deuxième ligne:
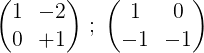
4- La première ligne est multipliée par ½:

5- Le deuxième et le premier ajoute et le résultat est placé à la première rangée:
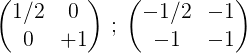
6- Pour terminer le processus, la première ligne par 2 est multipliée pour obtenir dans la première la matrice d'identité et dans la seconde la matrice inverse de la matrice d'origine M:
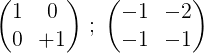
C'est-à-dire:
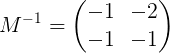
Solution système
Une fois la matrice inverse obtenue, le système d'équations est résolu en appliquant la matrice inverse dans les deux membres de l'équation du vecteur compact:
M-1M x = m-1B
X = m-1B
Qui reste explicitement comme ceci:
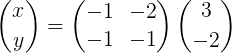
Ensuite, la multiplication matricielle est faite pour obtenir le vecteur x:
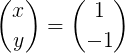
Méthode 2: par matrice attachée
Dans cette deuxième méthode, la matrice inverse est calculée sur la base de la matrice attachée de la matrice d'origine POUR.
Supposons une matrice donnée par:

oùI, J C'est l'élément de la ligne Toi et la colonne J de la matrice POUR.
L'attachement de la matrice POUR Il sera appelé Adj (a) Et ses éléments sont:
PUBLICITÉI, J = (-1)(i + j) ¦ai, j¦
où Ai, J Il s'agit de la matrice mineure complémentaire qui est obtenue en éliminant la ligne I et la colonne J de la matrice d'origine POUR. Barres ¦ ¦ Indiquez que le déterminant est calculé, c'est-à-dire ¦ai, j¦ C'est le déterminant de la matrice mineure complémentaire.
Peut vous servir: côtés homologuesFormule de matrice inverse
La formule pour trouver la matrice inverse basée sur la matrice attachée de la matrice d'origine est la suivante:
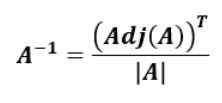
C'est-à-dire la matrice inverse de POUR, POUR-1, est la transposition de l'attachement de POUR divisé par le déterminant de POUR.
Le transposé POURTd'une matrice POUR C'est celui obtenu en échangeant des rangs contre des colonnes, c'est-à-dire que la première ligne devient la première colonne et la deuxième ligne de la deuxième colonne et ainsi de suite jusqu'à les lignes N de la matrice d'origine.
Exercice résolu
Être la matrice à la suivante:
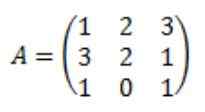
Chacun des éléments de la matrice attachée de a: adj (a) sont calculées
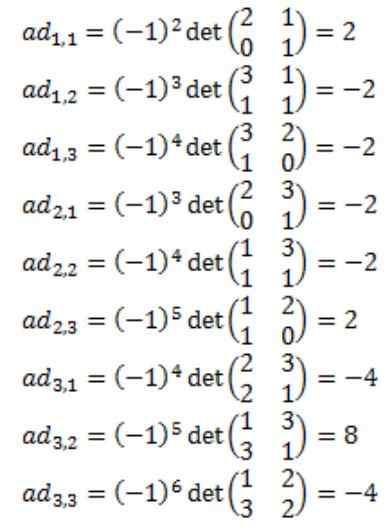
Résultant que la matrice attachée de A, adj (a) est la suivante:
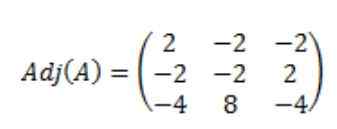
Ensuite, le déterminant de la matrice A, DET (A) est calculé:
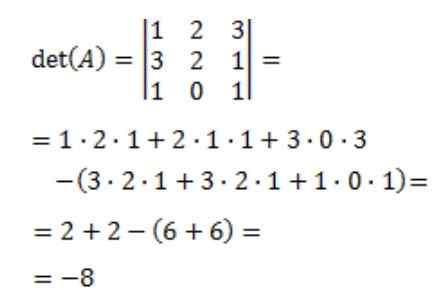
Enfin, la matrice inverse de A est obtenue:
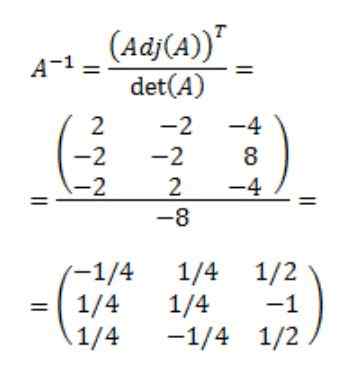
Les références
- Anthony Nicolaides (1994) Déterminants et matrices. Publication de passage.
- Awol Assen (2013) Une étude sur le calcul des déterminants de 3 × 3
- Casteleiro Villalba M. (2004) Introduction à l'algèbre linéaire. Éditorial ESIC.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Maths: A Student's Survival Guide. la presse de l'Universite de Cambridge.
- Richard J. Brown (2012) Maths de 30 secondes: les 50 théories les plus exprimées en mathématiques. Ivy Press Limited.
- Matrice. Lap Lambert Academic Publishing.
- « Caractéristiques de demi-culture moyennes, types, utilisations
- Description du calendrier mayan, comment fonctionne, les systèmes »

