Loi de la formule Lenz, équations, applications, exemples

La Loi de Lenz Il établit que la polarité de la force électromotrice induite dans un circuit fermé, en raison de la variation de l'écoulement du champ magnétique, est telle qu'elle s'oppose à la variation dudit flux.

Le signe négatif qui est mis à la loi de Faraday, prend en considération la loi de Lenz, étant la raison pour laquelle elle est appelée la loi de Faraday-Lenz et qui est exprimée comme suit:

Figure 1. Une bobine toroïdale est capable d'induire des courants dans d'autres conducteurs. Source: Pixabay.

[TOC]

Formules et équations

ε représente la force électromotrice induite, abrégée comme Femelle, Φ C'est le flux de champ magnétique et t C'est le moment. Unités dans le système international (SI) pour Femelle Ce sont les volts (v).

Pour sa part, le flux de champ magnétique Φ Il est défini par le produit scalaire suivant:

Tellement B comme n Ce sont des amplitudes vectorielles et peuvent être indiquées avec audacieuse ou avec une flèche sur la lettre. B C'est le vecteur de champ magnétique et n C'est le vecteur unitaire (magnitude égale à 1) perpendiculaire à la surface croisée par B.

Dans l'équation montrée B Il est constant et l'unité pour Φ Dans le SI pour le champ magnétique, le flux est le Weber (W):

1 Weber = 1 Tesla. mètre²

Une autre façon d'exprimer Φ C'est celui obtenu en utilisant la définition du produit scalaire:

Φ = b.POUR.cos θ

Dans cette équation, B C'est l'ampleur du champ magnétique (sans gras ni flèche, pour distinguer le vecteur de son ampleur), a est la zone de la surface traversée par le champ et θ est l'angle entre les vecteurs B et n.

Le flux de champ magnétique peut être varié de différentes manières dans le temps, pour créer un Femelle induit dans une boucle - un circuit fermé - de la surface à. Par exemple:

-Faire la variable du champ magnétique dans le temps: B = B (T), Garder la zone et l'angle constant, puis:

-La zone spase peut varier, laissant les autres amplitudes constantes:

 -L'angle entre B Et la surface est variée par la rotation de la spase, de cette manière un générateur sinusoïdal est obtenu:

Mieux encore, au lieu d'une seule boucle, les Nougas sont utilisés, dans ce cas le Femelle Multipliez n fois:

 Bien sûr, le flux de champ magnétique peut varier avec n'importe quelle combinaison de ces formes, bien qu'il soit un peu plus compliqué de décrire.

Applications

L'application immédiate de la loi de Lenz est de déterminer la signification du Femelle ou le courant induit sans avoir besoin d'effectuer un calcul. Considérez ce qui suit: vous avez une boucle au milieu d'un champ magnétique, comme celui qui produit un aimant de barre.

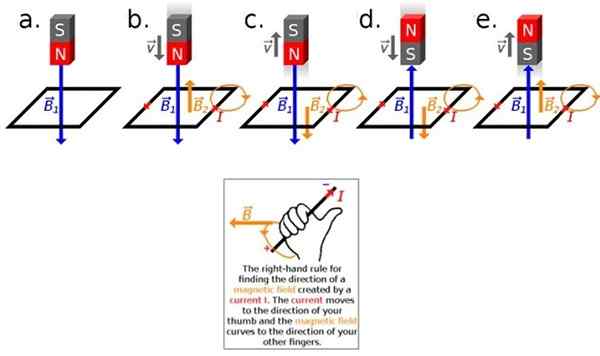Figure 2. Application de la loi de Lenz. Source: Wikimedia Commons.

Si l'aimant et la boucle sont au repos un par rapport à l'autre rien ne se passe, c'est-à-dire qu'il n'y aura pas de courant induit, car l'écoulement du champ magnétique reste constant dans ce cas (voir figure 2A). Pour induire le courant, il est nécessaire que le flux varie.

Maintenant, s'il y a un mouvement relatif entre l'aimant et la spase, déplaçant l'aimant vers la spase, soit vers l'aimant, il y aura un courant induit pour mesurer (figure 2B).

Ce courant induit génère à son tour un champ magnétique, donc nous aurons deux champs: celui de l'aimant B₁ en bleu et celui associé au courant créé par induction B₂, en orange.

La règle du pouce droit vous permet de connaître la direction de B₂, Pour ce faire, le pouce de la main droite est placé dans la direction et la direction que le courant a. Les quatre autres doigts indiquent la direction dans laquelle le champ magnétique est incurvé, selon la figure 2 (ci-dessous).

Peut vous servir: miroir convexe

Mouvement de l'aimant à travers la spase

Disons que l'aimant est tombé vers la boucle avec son pôle nord dirigé vers lui (figure 3). Les lignes de champ de l'aimant quittent le pôle Nord et entrent dans le poteau sud. Il y aura donc des changements dans φ, le flux créé par B₁ qui traverse la boucle:Φ augmentation!  Par conséquent, dans la boucle, un champ magnétique est créé B₂ Avec une intention opposée.

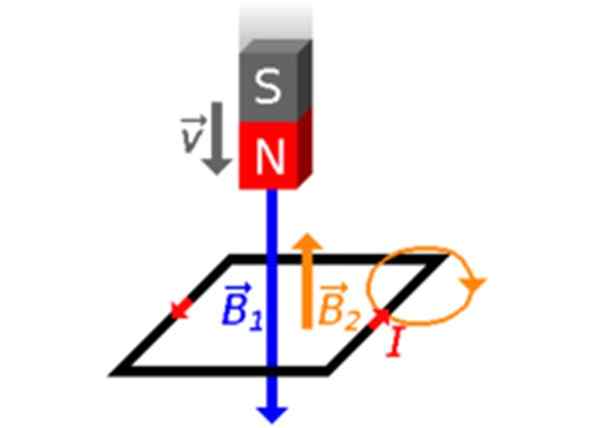figure 3. L'aimant se déplace vers la boucle avec son pôle nord. Source: Wikimedia Commons.

Le courant induit a un sens contraire aux aiguilles d'horloge, -fléchas rouges sur les figures 2 et 3-, selon la règle du pouce droit.

Éloignons de l'aimant de Spira et de son Φ diminue (figures 2c et 4), donc la boucle est rapide pour créer un champ magnétique à l'intérieur B₂ De la même manière, pour compenser. Par conséquent, le courant induit est le temps, comme le montre la figure 4.

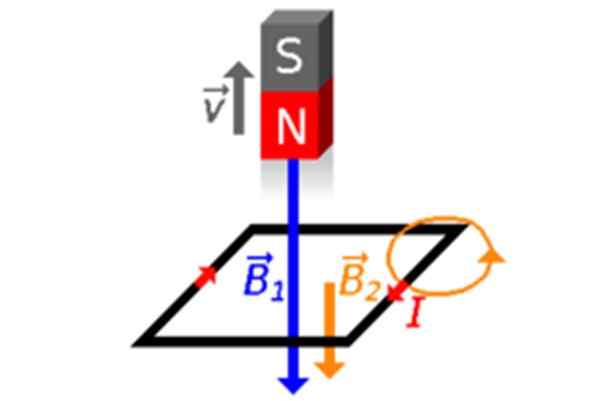Figure 4. L'aimant s'éloigne de la boucle, toujours avec son pôle nord le pointant vers elle. Source: Wikimedia Commons.

Investir la position de l'aimant

Que se passe-t-il si la position de l'aimant est investie? Si le pôle Sud pointe vers la boucle, le champ pointe vers le haut, puisque les lignes de B Dans un aimant, ils quittent le pôle Nord et entrent dans le pôle Sud (voir figure 2d).

Immédiatement, la loi de Lenz informe que ce champ vertical vers le haut, se précipitant vers la boucle, induira un champ opposé à ce sujet, c'est-à-dire, B₂ en bas et le courant induit sera également le temps.

Enfin, il s'éloigne de l'aimant de La Espira, toujours avec son pôle Sud pointant vers l'intérieur de ce. Puis à l'intérieur de la boucle, il y a un champ B₂ Pour contribuer à la suppression de l'aimant ne pas modifier le flux de champ dedans. Tellement B₁ comme B₂ Ils auront la même signification (voir figure 2D).

Le lecteur se rendra compte que, comme nous l'avons promis, aucun calcul n'a été fait pour connaître la direction du courant induit.

Expériences

Heinrich Lenz (1804-1865) a effectué de nombreuses œuvres expérimentales tout au long de sa carrière scientifique. Les plus connus sont ce que nous venons de décrire, se consacrant à mesurer les forces et les effets magnétiques créés en laissant brusquement un aimant au milieu d'une boucle. Avec ses résultats, il a affiné le travail réalisé par Michael Faraday.

Ce signe négatif dans la loi de Faraday s'avère être l'expérience pour laquelle il est le plus reconnu aujourd'hui. Cependant, Lenz a fait de nombreux emplois en géophysique pendant sa jeunesse et, en attendant, il s'est consacré à abandonner les aimants à l'intérieur des virages et des tubes. Il a également étudié la résistance électrique et la conductivité des métaux.

En particulier, sur les effets de l'augmentation de la température de la valeur de résistance. Il a continué à observer que lors du chauffage d'un fil, la résistance diminue et dissipe la chaleur, quelque chose que James Joule a également observé indépendamment.

Pour se souvenir toujours de leurs contributions à l'électromagnétisme, en plus de la loi qui porte son nom, aux inductances (bobines), elles sont indiquées avec la lettre L.

Peut vous servir: Théorème de Thévenin: ce qui consiste, les applications et les exemples

Tube de Lenz

C'est une expérience dans laquelle il est démontré comme un aimant s'arrête lorsqu'il est libéré à l'intérieur d'un tube en cuivre. L'aimant à la chute, génère des variations dans l'écoulement du champ magnétique à l'intérieur du tube, comme c'est le cas avec la spirale de puissance.

Alors un courant induit est créé qui s'oppose au changement de flux. Le tube crée son propre champ magnétique pour cela, qui comme nous le savons déjà, est associé au courant induit. Supposons que l'aimant est libéré avec le pôle Sud en bas (2d et 5).

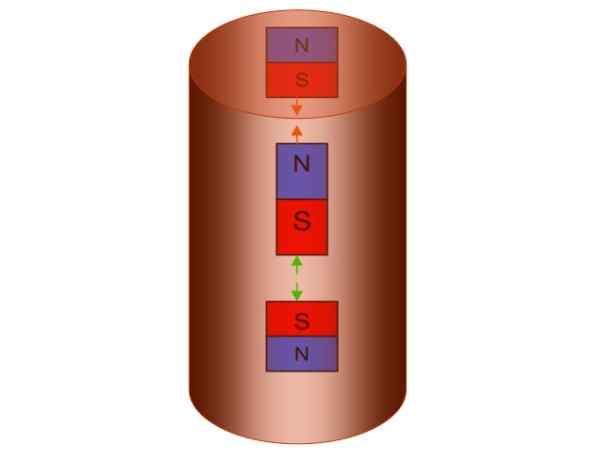Figure 5. Tube de Lenz. Source: F. Zapata.

En conséquence, le tube crée son propre champ magnétique avec un pôle Nord vers le bas et un pôle Sud en haut, ce qui équivaut à créer quelques aimants fictifs, un au-dessus et un autre sous celui qui tombe.

Le concept est incarné dans la figure suivante, mais il faut se rappeler que les poteaux magnétiques sont inséparables. Si l'aimant fictif inférieur a un pôle nord en bas, il accompagnera nécessairement un sud vers le sud.

Alors que les pôles opposés s'attirent et que les opposés se repoussent, l'aimant qui tombe sera repoussé, et en même temps attiré par l'aimant fictif supérieur.

L'effet net sera toujours freiné même si l'aimant est libéré avec le pôle Nord en bas.

Loi Joule-Lenz

La loi Joule-Lenz décrit comme faisant partie de l'énergie associée au courant électrique qui circule par un conducteur est perdue sous forme de chaleur, un effet utilisé dans les radiateurs électriques, les assiettes, les sèche-cheveux et la cuisinière électrique, entre autres appareils électroménagers.

Tous ont une résistance, un filament ou un élément de chauffage qui se réchauffe jusqu'au passage du courant.

Sous forme mathématique, que ce soit R La résistance de l'élément chauffant, Toi l'intensité de courant qui circule à travers elle et t Le temps, la quantité de chaleur produite par Joule Effect est:

Q = I². R. t

Où Q Il est mesuré en joules (unités SI). James Joule et Heinrich Lenz ont découvert cet effet simultanément vers 1842.

Exemples

Ci-dessous, nous montrons trois exemples importants dans lesquels la loi de Faraday-Lenz est appliquée:

Générateur de courant alternatif

Un générateur de courant alternatif transforme l'énergie mécanique en énergie électrique. La fondation a été décrite au début: une boucle est tournée au milieu d'un champ magnétique uniforme, comme celui qui est créé entre les deux pôles d'un grand électroaim. Lorsqu'elle est utilisée N spirales, le Femelle augmente proportionnellement à N.

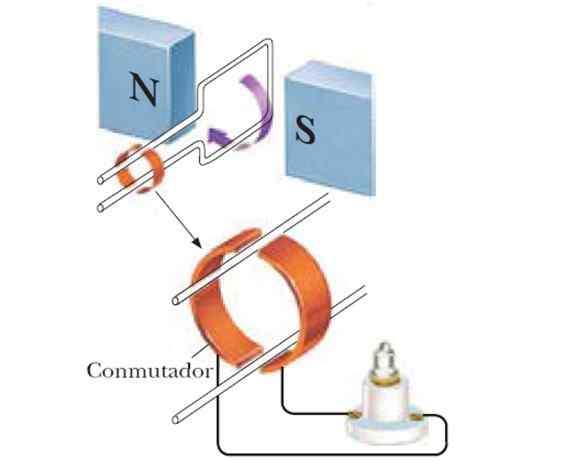Figure 6. Le générateur de courant alternatif.

Au fur et à mesure que la boucle est tournée, le vecteur normal à sa surface modifie son orientation par rapport au champ, produisant un Femelle qui varie de manière sinusoïdale au fil du temps. Supposons que la fréquence angulaire de rotation soit Ω, Ensuite, lors du remplacement de l'équation qui s'est produite au début, ce sera:

Le transformateur

C'est un appareil qui vous permet d'obtenir une tension directe à partir d'une tension alternative. Le transformateur fait partie d'innombrables appareils, comme un chargeur de téléphone portable, par exemple.Cela fonctionne de la manière suivante:

Il y a deux bobines roulées autour d'un noyau de fer, un est appelé primaire et l'autre secondaire.  Le nombre respectif de tours est n₁ et n₂.

La bobine ou l'enroulement primaire est connecté à une tension alternative (comme l'électricité maison, par exemple) du formulaire V_P = V₁.cos ωt, provoquant la circulation d'un courant de fréquence alternatif Ω.

Ce courant provient d'un champ magnétique qui à son tour provoque un flux magnétique oscillant dans la deuxième bobine ou l'enroulement, avec une tension secondaire de la forme V_S = V₂.cos ωt.

Cependant, il s'avère que le champ magnétique à l'intérieur du noyau de fer est proportionnel à l'inverse du nombre de tours de l'enroulement primaire:

Il peut vous servir: 13 exemples de la deuxième loi de Newton dans la vie quotidienne

B ∝ 1 / n₁

Et donc ce sera V_P, la tension dans l'enroulement primaire, tandis que le Femelle induit V_S Dans le deuxième enroulement, il est proportionnel, comme nous le savons, au nombre de tours n₂ et aussi à V_P.

Ainsi, en combinant ces proportionnalités, il existe une relation entre V_S et V_P qui dépend du quotient entre le nombre de virages de chacun, comme suit:

V_S = (N₂ / N₁) V_P

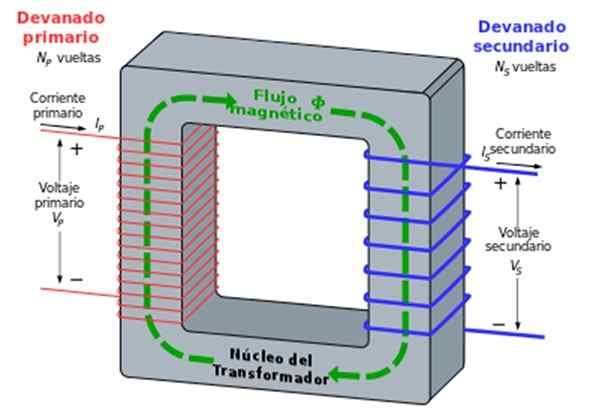Figure 7. Le transformateur. Source: Wikimedia Commons. Kundalizizero [cc by-sa 3.0 (http: // CreativeCommons.Org / licences / by-sa / 3.0 /]]

Le détecteur de métaux

Ce sont des appareils utilisés dans les banques et les aéroports de sécurité. Ils détectent la présence de tout métal, pas seulement du fer ou du nickel. Ils fonctionnent grâce aux courants induits, grâce à l'utilisation de deux bobines: un émetteur et un autre récepteur.

Un courant à haute fréquence alternatif est passé dans la bobine de transmission, de sorte qu'il génère un champ magnétique alternatif le long de l'axe (voir figure), qui induit un courant dans la bobine de réception, quelque chose de plus ou moins similaire à ce qui se passe avec le transformateur.

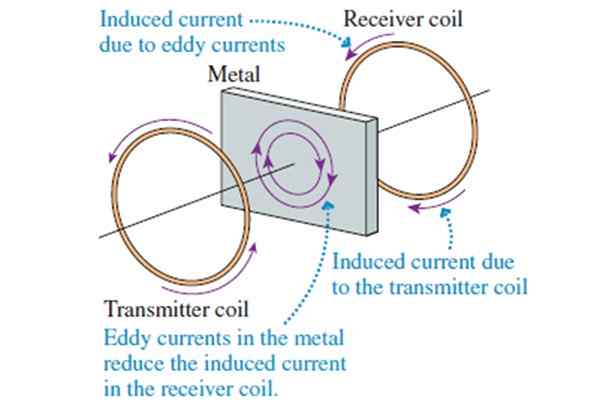Figure 8. Principe d'opération de détecteur de métaux.

Si un morceau de métal est placé entre les deux bobines, les petits courants induits y apparaissent, appelés courants Foucault (qui ne peuvent pas circuler dans un isolant). La bobine de réception répond aux champs magnétiques de la bobine d'émission et à ceux créés par les courants de Foucault.

Les courants Foucault essaient de minimiser le flux de champ magnétique dans la pièce métallique. Par conséquent, le champ qui perçoit la bobine de réception diminue lors de l'interposition à une pièce métallique entre les deux bobines. Lorsque cela se produit une alarme qui avertit la présence d'un métal.

Exercices

Exercice 1

Il y a une bobine circulaire avec 250 entreprises de rayon de 5 cm, situées perpendiculaires à un champ magnétique de 0.2 T. Détermine le Femelle induit si dans un intervalle de temps de 0.1 s, le champ magnétique magnétique double et indiquant la signification du courant, selon la figure suivante:

Figure 9. Spira circulaire au milieu d'un champ magnétique uniforme perpendiculaire au plan spase. Source: F. Zapata.

Solution

Nous allons d'abord calculer l'ampleur de la FEM induite, puis la signification du courant associé sera indiquée en fonction du dessin.

N = 250 tours

A = π. R² = P . (5 x 10^-2 m)² = 0.0079 m².

cos θ = cos 0 = 1 (Le vecteur n Il faut parallèle à B)

Alors que le champ magnétique double son ampleur, vous avez:

Remplacer ces valeurs dans l'équation pour l'ampleur du Femelle Induit:

ε = 250. 0.0079 m² . 2 t / s = 3.95 V

Depuis que le champ a doublé, le flux de champ magnétique a fait de même, donc dans la boucle, un courant induit est créé qui s'oppose à ladite augmentation.

Le champ de la figure pointe vers l'écran. Le champ créé par le courant induit doit quitter l'écran, en appliquant la règle du pouce droit, il s'ensuit que le courant induit est anti-horaire.

Exercice 2

Un enroulement carré est composé de 40 tours de 5 cm côté, qui tourne fréquemment 50 Hz au milieu d'un champ de grandeur uniforme 0.1 T. Initialement, la bobine est perpendiculaire au champ. Quelle sera l'expression pour le Femelle induit?

Solution

À partir des sections précédentes, cette expression a été déduite:

ε = n.B.POUR. Ω. péché Ωt

A = (5 x 10^-2 m)² = 0.0025 m²

N = 40 spirales

Ω = 2π.F = 2π.50 Hz = 100p s^-1

B = 0.1 T

ε = 40 x 0.1 x 0.0025 x 100π  x Sen 50.t =p . Sen 100π.la télé

Les références

1. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 6. Électromagnétisme. Édité par Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Sciences physiques conceptuelles. 5e. Élégant. Pearson.
3. Chevalier, r.  2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique. Pearson.
4. Collège openx. Loi de Faraday sur l'induction: la loi de Lenz. Récupéré de: OpenTextBC.CA.
5. Bibliothèque de physique. Loi de Lenz. Récupéré de: Phys.Bibliothèque.org.
6. Sears, f. (2009). University Physics Vol. 2.