Loi de Gauss

Nous expliquons ce qu'est la loi de Gauss, ses applications et avons mis des exercices résolus

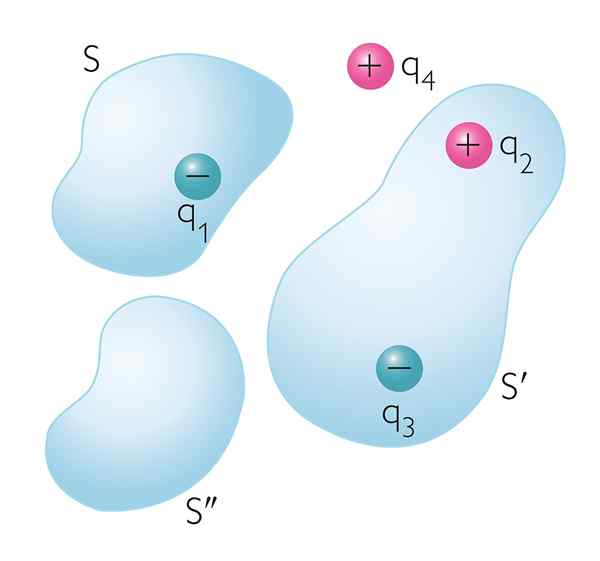
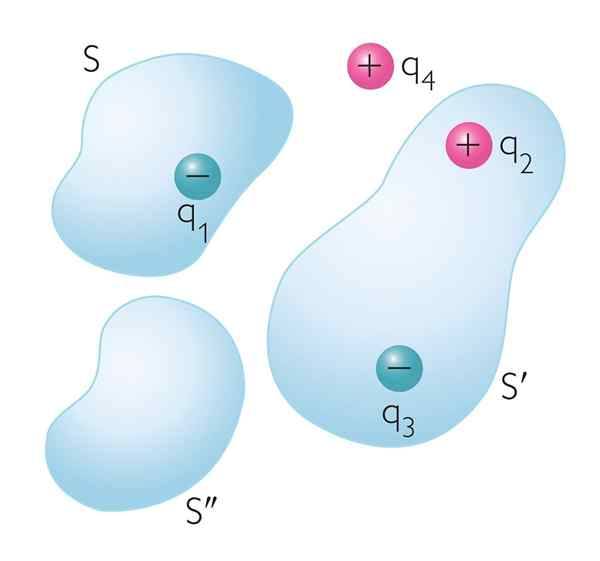Figure 1. Les charges électriques à l'intérieur et à l'extérieur des surfaces gaussiennes arbitrairement. Seules les charges verrouillées à l'intérieur de chaque surface contribuent à l'écoulement électrique net à travers eux

Quelle est la loi de Gauss?

La Loi de Gauss indique que l'écoulement du champ électrique, à travers une surface fermée imaginaire, est proportionnelle à la valeur de charge nette des particules trouvées à l'intérieur de cette surface.

Dénotant l'écoulement électrique à travers une surface fermée comme Φ_ET et à la charge nette verrouillée par la surface par Q_enf, Ensuite, la relation mathématique suivante est établie:

Φ_ET = C ∙ Q_enf

Où c C'est la constante de proportionnalité.

Explication de la loi de Gauss

Pour comprendre le sens de la loi de Gauss, il est nécessaire d'expliquer les concepts impliqués dans sa déclaration: charge électrique, champ électrique et flux de champ électrique à travers une surface.

Charge électrique

La charge électrique est l'une des propriétés fondamentales de la matière. Un objet chargé peut avoir l'un des deux types de charge: positif ou négatif, bien que normalement les objets soient neutres, c'est-à-dire qu'ils ont la même quantité de charge négative que positive.

Deux objets chargés de chargement du même type sont repoussés même lorsqu'il n'y a pas de contact les uns avec les autres et est dans le vide. Au contraire, lorsque chacun des corps a de nombreuses signes différents, alors ils attirent. Ce type d'interaction de distance est connu sous le nom d'interaction électrique.

Dans le système international d'unités si la charge électrique est mesurée Culombios (C). Le porteur de cargaison élémentaire négatif est le électron Avec chargement de -1,6 x 10^-19C Et le porte-charge élémentaire positif est le proton avec une valeur de charge +1,6 x 10^-19C. Les corps généralement chargés ont entre dix^-9C et dix^-3C.

Champ électrique

Un corps chargé électrique modifie l'espace dans son environnement, le remplissant de quelque chose d'invisible appelé champ électrique. Pour savoir que ce champ est présent, une charge de test spécifique est requise.

Peut vous servir: mouvement harmonique simple

Si la charge d'essai est placée dans un endroit où il y a un champ électrique, une force apparaît sur une certaine direction, qui est la même que celle du champ électrique. L'intensité du champ est la force sur la charge d'essai divisée par la quantité de charge. Ensuite, les unités de champ électrique ET Dans le système international d'unités Newton entre Coulomb: [E] = n / c.

Les charges spécifiques positives produisent un champ radial à l'extérieur, tandis que les charges négatives produisent un champ dirigée radialement vers l'intérieur. De plus, le champ produit par une charge ponctuelle se désintègre avec l'inverse du carré de la distance à ladite charge.

Lignes de champ électrique

Michael Faraday (1791 - 1867) a été le premier à avoir une image mentale du champ électrique, l'imaginant comme des lignes qui suivent la direction du champ. Dans le cas d'une charge ponctuelle positive, ces lignes sont radiales à partir du centre. Où les lignes sont plus ensemble, le champ est plus intense et moins intense où ils sont plus séparés.

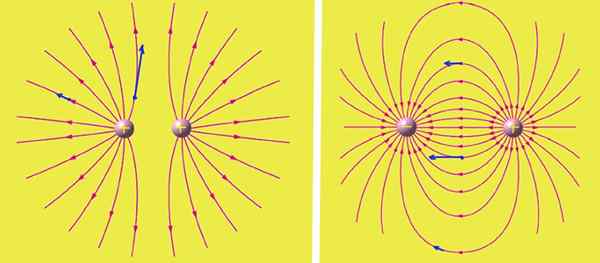Figure 2. Sur les lignes de champ gauche de deux charges égales et positives. À droite, les lignes de champ de chargement égales, mais signes contraires. Les flèches bleues représentent le vecteur de champ électrique dans différentes positions. Source: Wikimedia Commons.

Les charges positives sont les sources d'où émergent les lignes de champ électrique, tandis que les charges négatives sont les puits des lignes.

Les lignes de champ électrique ne se ferment pas sur elles-mêmes. Dans un ensemble de charges, les lignes laissent les charges positives et entrent les positives, mais elles peuvent également arriver ou venir de l'infini.

Peut vous servir: équilibre stable: concept et exemples

Ils ne se croisent pas non plus et à chaque point de l'espace, le vecteur de champ électrique est tangent à la ligne de champ et proportionnel à la densité de ligne là-bas.

figure 3. La fille est chargée électriquement d'être en contact avec le dôme d'un générateur de van der Graaf. Vos cheveux suivent les lignes de champ électrique. Source: Wikimedia Commons.

Flux de champ électrique

Les lignes de champ électrique ressemblent aux lignes actuelles d'une rivière qui s'écoule doucement, à partir de là, le concept de flux de champ électrique est né.

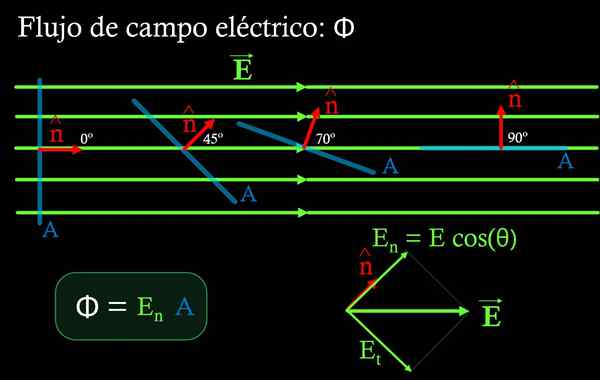Figure 4. L'écoulement du champ électrique à travers une surface de zone A dépend de l'angle formé entre ladite surface et le champ et. L'écoulement maximal est obtenu lorsque la surface est perpendiculaire au champ et que l'écoulement est nul lorsque la surface est parallèle au champ. Source: F. Zapata.

Dans une région où le champ électrique est uniforme, l'écoulement φ à travers une surface plane est le produit de la composante normale du E_n à cette surface, multipliée par la zone POUR de la même:

Φ = e_n ∙ A

Composant E_n Il est obtenu en multipliant l'amplitude du champ électrique par le cosinus de l'angle formé entre le champ et le vecteur d'unité normal à la surface de la zone POUR. (Voir figure 4).

Gaussh Law demandes

La loi de Gauss peut être appliquée pour déterminer le champ électrique produit par les distributions de charge avec un haut degré de symétrie.

Champ électrique d'une charge ponctuelle

Une charge ponctuelle produit un champ électrique radial qui est sortant si la charge est positive et entrante autrement.

Choisir en tant que surface gaussienne Une sphère imaginaire de radio r et concentrique à la charge Q, à tous les points de la surface de ladite sphère, le champ électrique est de même ampleur et sa direction est toujours normale à la surface. Ensuite, dans ce cas, le flux de champ électrique est le produit de l'ampleur du champ par la surface totale de la surface sphérique:

Peut vous servir: Mécanique des fluides: histoire, quelles études, fondamentaux

Φ = e ∙ a = e ∙ 4πr²

D'un autre côté, la loi de Gauss établit que: φ = c ∙ q, étant la constante de proportionnalité c. Lorsque vous travaillez dans les unités du système des mesures internationales, la constante c C'est l'inverse de l'allocation du vide, et la loi de Gauss est formulée comme suit:

Φ = (1 / ε_soit) ∙ Q

L'intégration du résultat obtenu pour le flux vers la loi de Gauss est:

E ∙ 4πr² = (1 / ε_soit) ∙ Q

Et pour l'ampleur de ET résultat:

E = (1/4πε_soit) ∙ (Q / R²)

Coïncide entièrement avec la loi Coulomb du champ électrique d'une charge ponctuelle.

Exercices

Exercice 1

Deux charges spécifiques se trouvent dans une surface gaussienne s arbitraire. On sait que l'un d'eux a une valeur de +3 NC (3 nano-coulomb). Si le champ électrique net s'écoule à travers la surface gaussienne est de 113 (n / c) m², Quelle sera la valeur de l'autre charge?

Solution

La loi de Gauss établit que

Φ_ET = (1 / ε_soit) ∙ Q_enf

De là, la charge nette verrouillée est:

Q_enf = Φ_ET ∙ ε_soit

Remplacement des résultats des données:

Q_enf = 113 (n / c) m² ∙ 8,85 x 10^-12 (C² m^-2 N^-1) = 1 x 10^-9 C = 1 NC.

Mais Q_enf = + Q - q, Lorsque la charge positive a une valeur connue de +3 nc, par conséquent, la charge sera nécessairement -2 NC.

Exercice 2

Dans la figure 2, il y a un arrangement (à gauche) de deux charges positives, chacune avec valeur + Q et une autre arrangement (à droite) avec une charge + Q et l'autre -Q. Chaque arrangement est verrouillé dans une boîte imaginaire avec tous ses bords de 10 cm. Oui | Q | = 3 μC, trouvez le flux de champ électrique net à travers la boîte pour chaque arrangement.

Solution

Dans le premier arrangement, le flux net est:

Φ_ET = (1 / ε_soit) ∙ (+ q + q) = 678000 (n / c) m²

Dans la bonne disposition, le flux net à travers la boîte imaginaire contenant le couple des charges est nul.

Les références

1. Cosenza, M. Électromagnétisme. Université des Andes.
2. Díaz, R. Électrodynamique: notes de classe. Université nationale de Colombie.
3. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 6. Électromagnétisme. Édité par Douglas Figueroa (USB).
4. Jackson, J. D. Électodynamique classique. 3e. Élégant. Wiley.
5. Tarazona, C. Introduction à l'électrodynamique. Université éditoriale Manuela Beltrán.