Faraday Formula Loi, unités, expériences, exercice,

La Loi de faraday Dans l'électromagnétisme, il établit qu'un flux de champ magnétique changeant est capable d'induire un courant électrique dans un circuit fermé.

En 1831, le physicien anglais Michael Faraday a connu des conducteurs en mouvement à l'intérieur d'un champ magnétique et des champs magnétiques variant également qui ont traversé les conducteurs fixes.

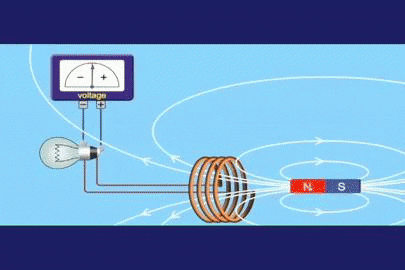Figure 1. Expérience à induction de Faraday

Faraday s'est rendu compte que s'il variait le flux de champ magnétique dans le temps, il a pu établir une tension proportionnelle à ladite variation. Si ε est la tension ou la force électromotrice induite (FEM induite) et que φ est le flux de champ magnétique, sous forme mathématique, il peut être exprimé:

| ε | = Δφ / Δt

Où le symbole δ indique la variation de la quantité et les barres dans la FEM indiquent la valeur absolue de ce. Puisqu'il s'agit d'un circuit fermé, le courant peut circuler dans un sens ou un autre.

Le flux magnétique, produit par un champ magnétique à travers une surface, peut varier de différentes manières, par exemple:

-Déplacer un aimant à barre à travers une spirale circulaire.

-Augmenter ou diminuer l'intensité du champ magnétique qui traverse la boucle.

-Laissant le champ fixe, mais par un mécanisme change la zone de la boucle.

-Combiner les méthodes ci-dessus.

Figure 2. Le physicien anglais Michael Faraday (1791-1867).

[TOC]

Formules et unités

Supposons qu'il y ait un circuit fermé de la zone A, comme une spirale circulaire ou un assurge égal à la figure 1, et qu'il existe un aimant qui produit un champ magnétique B.

Le flux de champ magnétique φ est une quantité scalaire qui fait référence à la quantité de lignes de champ qui traversent la zone A. Dans la figure 1, les lignes blanches quittent le pôle nord de l'aimant et reviennent au sud.

Peut vous servir: Brayton Cycle: processus, efficacité, applications, exercices

L'intensité du champ sera proportionnelle au nombre de lignes par unité de surface, nous pouvons donc voir qu'à la pôle, il est très intense. Mais nous pouvons avoir un champ très intense qui ne produit pas de flux dans la boucle, que nous pouvons réaliser en modifiant l'orientation de cette (ou de l'aimant).

Pour prendre en compte le facteur d'orientation, le flux de champ magnétique est défini comme le produit scalaire entre B et n, être n Le vecteur unitaire normal à la surface de la spase et qui indique son orientation:

Φ = B•n A = ba.cosθ

Où θ est l'angle entre B et n. Si par exemple B et n Ils sont perpendiculaires, l'écoulement du champ magnétique est vide, car dans ce cas, le champ est tangent au plan spase et ne peut pas traverser sa surface.

Plutôt B et n Ils sont parallèles, cela signifie que le champ est perpendiculaire au plan Spira et que les lignes le traversent au maximum.

L'unité du système international pour F est le Weber (W), où 1 w = 1 t.m² (lit "Tesla par mètre carré").

Loi de Lenz 

Dans la figure 1, nous pouvons voir que la polarité de la tension change à mesure que l'aimant se déplace. La polarité est établie par la loi de Lenz, qui stipule que la tension induite doit s'opposer à la variation qui le produit.

Si, par exemple, le flux magnétique produit par l'aimant augmente, le conducteur établit un courant qui circule en créant son propre flux, qui s'oppose à cette augmentation.

Si, au contraire, l'écoulement créé par l'aimant diminue, le courant induit circule de telle manière que son propre débit contrecarte dit diminuer.

Peut vous servir: échelles thermométriques

Pour prendre en compte ce phénomène, un signe négatif à la loi de Faraday est mis avant et il n'est plus nécessaire de placer les barres de valeur absolue:

ε = -Δφ / Δt

C'est la loi de Faraday-Lenz. Si la variation de l'écoulement est infinitésimale, les deltas sont remplacés par des différentiels:

ε = -dφ / dt

L'équation précédente est valable pour une boucle. Mais si nous avons une bobine de rotation, le résultat est bien meilleur, car le FEM se multiplie n fois:

ε = - n (dφ / dt)

Expériences de Faraday

Pour produire le courant qui allume l'ampoule, entre l'aimant et la spirale, il doit y avoir un mouvement relatif. C'est l'une des façons dont l'écoulement peut varier, car de cette manière l'intensité du champ qui traverse la boucle change.

Pour le moment, le mouvement de l'aimant cesse, l'ampoule s'éteint, même si l'aimant est resté immobile dans la spase. Ce qui est nécessaire pour faire circuler le courant vers l'ampoule, c'est que le flux de champ varie.

Lorsque le champ magnétique varie dans le temps, nous pouvons l'exprimer comme:

B = B (T).

En gardant la zone de la spase constante et en le laissant fixé à un angle constant, qui dans le cas de la figure est 0º, puis:

 Pour la boucle de la figure 1 (cos 0º = 1):

Spase de zone variable

Si vous pouvez changer la zone spase, en laissant sa fixation d'orientation et en la mettant au milieu d'un champ constant, la FEM induite est donnée par:

Une façon d'y parvenir est de mettre une barre qui glisse sur un rail conducteur à une certaine vitesse, comme le montre la figure suivante.

Peut vous servir: ío (satellite) figure 3. Générateur coulissant. Source: Serow, R. Physique pour la science et l'ingénierie.

La barre et le rail, plus une ampoule ou une résistance liée au fil du conducteur, forment un circuit fermé sous forme de spase rectangulaire.

Lorsque vous glissez la barre, la longueur X augmente ou diminue, et avec elle la zone de la boucle change, ce qui est suffisant pour créer un flux variable.

Variation du flux magnétique par rotation

Comme nous l'avons dit précédemment, si l'angle entre B Et la normale de la boucle est variée, le flux de champ change selon:

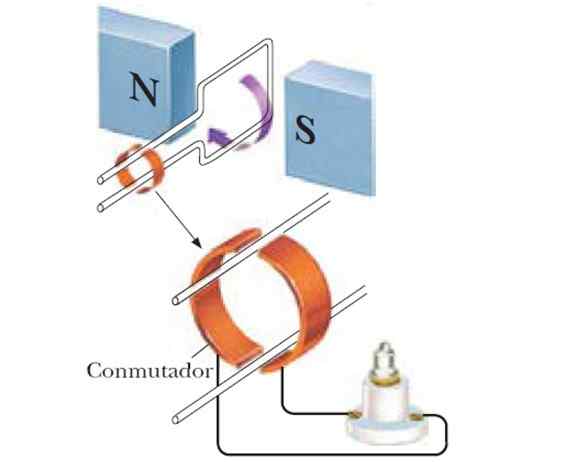Figure 4. Si la boucle est tournée parmi les pôles d'un aimant, un générateur sinusoïdal est obtenu. Source: F. Zapata.

Un générateur sinusoïdal est ainsi obtenu, et si un seul nombre de bobines est utilisée, la FEM induite est plus grande:

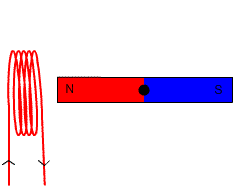Figure 5. Dans ce générateur, l'aimant est tourné pour induire le courant dans la bobine. Source: Wikimedia Commons.

Exercice résolu

Une bobine circulaire de n tours et de radio R, tourne angulairement ω au milieu d'un champ magnétique de grandeur b. Trouvez une expression pour la FEM induite maximale dans la bobine.

Solution

L'expression de la FEM induite par la rotation est appliquée lorsque la bobine a des tours, sachant que:

-La zone de la bobine est a = πr²

-L'angle θ varie en fonction du temps comme θ = ωt

Il est important de prendre en compte que θ = ωt est d'abord remplacé dans la loi de Faraday et alors Il dérive du temps:

ε = -nba (cos θ) '= -nb (πr²).[cos (ωt)] »= nbΩ (πr²) Sen (ωt)

Étant donné que la FEM maximale est demandée, cela se produit chaque fois que Sen ωt = 1, donc enfin:

ε_max = NbΩ (πr²)

Les références

1. Figueroa, D. 2005. Série: Physique pour la science et l'ingénierie. Volume 6. Électromagnétisme. Édité par Douglas Figueroa (USB).
2. Giambattista, un. 2010. La physique. Deuxième édition. McGraw Hill.
3. Giancoli, D.  2006. Physique: principes avec applications. 6e. Élégant. Prentice Hall.
4. Resnick, r. 1999. Physique. Vol. 2. 3e édition. en espagnol. Société de rédaction continentale S.POUR. de c.V.
5. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. 2ieme volume.