Droit de Darcy

Nous expliquons ce qu'est la loi de Darcy, ses équations, applications, limitations et proposent un exercice à résoudre

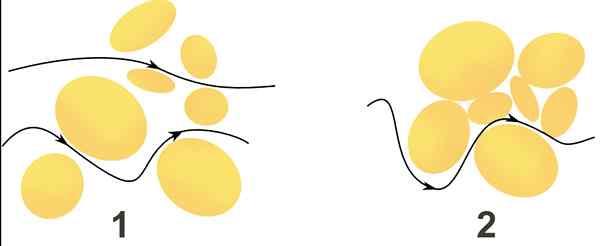
Le débit d'eau à travers deux milieux poreux est indiqué à travers des flèches noires. En milieu 1, le flux se déplace plus rapidement qu'au milieu 2, car la vitesse dépend de la taille des interstices et de la facilité de communication entre elles. Source: Wikimedia Commons.

Quelle est la loi de Darcy?

La Droit de Darcy Il s'agit d'une relation mathématique applicable à l'écoulement des fluides dans des milieux perméables ou poreux, par exemple, l'eau qui se draine dans le sable.

Au fur et à mesure que le fluide progresse à travers le poreux, sa pression hydrostatique varie, en particulier elle est plus grande aux points les plus proches de la source et plus bas aux points les plus proches du drainage. De cette façon, le concept de gradient hydraulique apparaît, une quantité physique qui sera indiquée avec la lettre I.

D'un autre côté, le milieu poreux est caractérisé par une quantité appelée Conductivité hydraulique K. Il existe clairement une relation entre la porosité, déterminée par K, le gradient hydraulique I et l'écoulement par unité de section transversale q q.

La relation entre eux a été découverte par l'ingénieur hydraulique français Henry Darcy (1803-1858), qui était en charge de l'approvisionnement en eau de sa ville natale: Dijon.

La loi de Darcy a été présentée en 1856, dans un travail approfondi dans lequel les quantités physiques impliquées dans la loi sont détaillées, les expériences réalisées et très particulièrement un appareil appelé permémoir.

Équations de la loi Darcy

La loi de Darcy montre la relation entre plusieurs quantités physiques qui décrivent le flux à travers un milieu poreux. Cela indique que le débit d'eau Q qui se déplace par un certain moyen poreux est directement proportionnel à la section transversale percée et au gradient hydraulique Toi:

Q ∝ A ∙ I

Peut vous servir: mouvement rectiligne uniforme: caractéristiques, formules, exercices

La constante de proportionnalité est la perméabilité k de l'environnement poreux, également appelé Conductivité hydraulique. De cette façon, la loi de Darcy est présentée comme suit:

Q = k ∙ a ∙ i

Forme différentielle de la loi de Darcy

L'équation de Darcy peut être exprimée comme une relation différentielle entre le débit à chaque point et le gradient hydraulique local:

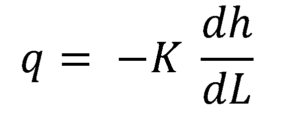
Comme le gradient hydraulique est une quantité négative lorsqu'elle est calculée dans le sens de l'écoulement, il est alors nécessaire de se multiplier par le négatif de la conductivité hydraulique pour obtenir le débit moyen Q, dans chaque section transversale.

Ensuite, les amplitudes présentes dans la loi de Darcy sont analysées plus en détail.

Débit, gradient hydraulique et perméabilité

1.- Flux q

L'écoulement est défini comme le volume d'eau qui circule à travers une certaine zone de section transversale à la direction de l'écoulement, par unité de temps:

Q = Δv / Δt

Dans le système international des unités SI, le débit est mesuré en mètres cubes par seconde, mais il est fréquemment exprimé en litres par minute ou des litres par seconde.

L'écoulement par unité de la zone Q est souvent requis, qui est le rapport entre le flux Q et la section transversale:

Q = Q / A

Dans le Si, Q est exprimé en m / s, c'est pourquoi Q représente la vitesse moyenne du fluide dans la section transversale du tuyau.

Il est important de noter que, bien que l'écoulement q soit le même dans toutes les sections du tuy.

2.- Gradient hydraulique I

Lorsqu'un fluide circule le long d'un milieu poreux, la pression hydrostatique diminue dans la même direction de l'écoulement.

Peut vous servir: ton: transformations, équivalences et exercices résolus

Il est connu que la pression hydrostatique, à un certain point du tuyau, est proportionnelle à la hauteur h qui marque un manomètre à tube ouvert à cet endroit. La constante de proportionnalité est le produit de la densité des fluides due à l'accélération de la gravité.

De cette façon, le gradient hydraulique I est défini comme le rapport entre la différence de hauteur ΔH des colonnes de deux manomètres et Δl, ce dernier étant la distance qui sépare les manomètres (voir la figure ci-dessous):

I = ΔH / Δl

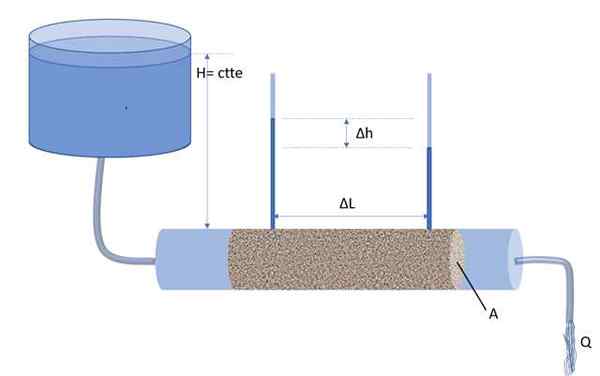Le permémoir, un appareil inventé par Henry Darcy pour quantifier l'écoulement de l'eau à travers un milieu poreux. Source: F. Zapata.

Il s'agit du gradient hydraulique moyen dans la section du long ΔL, une quantité sans dimension et aussi négatif.

Si vous souhaitez trouver le gradient hydraulique à chaque point du tuyau, la limite est prise pour ΔL tendant à zéro, entraînant la dérivée de la fonction de gradient hydraulique par rapport à la position L, le long de l'écoulement:

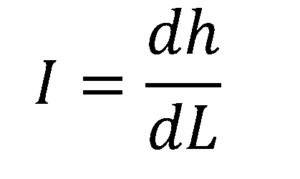
3.- Perméabilité k

La perméabilité d'une moyenne poreuse ou de conductivité hydraulique est le rapport entre l'écoulement Q et le produit de la section transversale POUR Pour le gradient hydraulique Toi:

K = q / a ∙ i

La conductivité hydraulique a des unités de vitesse, des mètres au-dessus d'elle-même.

Une unité pour K a été définie, appelée Darcy, En l'honneur d'Henry Darcy et défini comme suit:

UN Darcy C'est la perméabilité d'un millilitre fluide, avec une viscosité d'une centipoise, qui se déplace le long d'un centimètre dans une pression différentielle d'une atmosphère, à travers une section transversale d'un centimètre carré.

Demandes de droit de Darcy

La principale application de la loi de Darcy est de prédire l'écoulement de l'eau le long d'un aquifère, avant de former des puits.

Peut vous servir: analyse dimensionnelle

De plus, la loi de Darcy est régulièrement utilisée en génie agricole et hydrologique. Il peut également être utilisé dans l'industrie pétrolière pour décrire l'écoulement du gaz et du pétrole dans les milieux poreux. Cependant, dans ce cas, K peut varier, selon l'écoulement de gaz ou d'huile et ne peut pas dépendre uniquement et exclusivement du substrat perméable.

Limites

La loi de Darcy suppose que la conductivité hydraulique k est une quantité de médium, ce qui est vrai dans de nombreux cas. Cependant, parfois k dépend de la viscosité dynamique du fluide, qui à son tour peut dépendre du débit et des gradients de température.

L'hypothèse de Darcy est plausible lors de l'examen de l'eau souterraine, où la viscosité est pratiquement constante, car sa valeur n'est presque pas affectée compte tenu des quelques différences de température à travers l'aquifère.

En cas de débit d'huile par des moyens poreux, l'équation de Darcy ne peut pas être appliquée comme présenté ici, mais certaines modifications sont incorporées qui vont au-delà du but de cet article.

Exercice résolu

Déterminez la conductivité hydraulique d'un sable de plage, en utilisant un permétère de laboratoire.

Supposons que le tube du permémètre ait un diamètre de 20 cm et que la distance entre les deux manomètres est de 50 cm. Il est également connu que l'eau s'écoule à un taux de 300 décimètres cubes par minute et que la différence de niveau entre les deux manomètres est de 25 cm.

Solution

Le flux qui est de 300 décimètres cubes par minute, mais exprimant en unités du système international, ce serait comme ceci:

Q = 300 x 10^-3 m³ / 60 s = 5 x 10^-3 m³ /

La section transversale A est calculée par:

A = π ∙ r² = π ∙ (10 cm)² = π ∙ (0,1 m)² = 0,314 m²

Le gradient hydraulique I est un quotient entre la différence de hauteur manométrique et la séparation des manomètres:

I = 25 cm / 50 cm = 0,5

Selon la définition de la conductivité hydraulique k donnée ci-dessus:

K = q / a ∙ i = (5 x 10^-3 m³ / s) / (0,314 m² ∙ 0,5) = 3 185 x 10^-2 m / s ≈ 2 m / min.