Caractéristiques, types et exercices de l'objectif convergent résolu

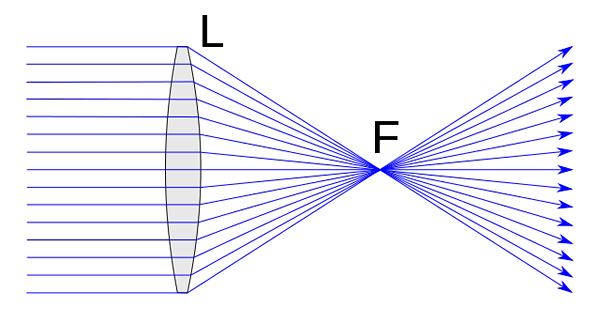
Le Lentilles convergentes Ce sont ceux qui sont plus épais dans leur partie centrale et plus mince sur les bords. En conséquence, ils se concentrent (convergent) en un seul point les rayons lumineux qui les affectent en parallèle à l'axe principal. Ce point est appelé focus ou focus d'image, et est représenté avec la lettre f. Des lentilles convergentes ou positives forment ce qu'on appelle les images réelles d'objets.

Un exemple de lentille convergente typique est une loupe. Cependant, il est courant de trouver ce type de lentilles sur des dispositifs beaucoup plus complexes tels que les microscopes ou les télescopes. En fait, un microscope à composé de base est celui constitué de deux lentilles convergentes qui ont une petite distance focale. Ces lentilles sont appelées cibles et oculaires.

Gagnifuling The pendant, une lentille convergente. 

Les lentilles convergentes sont utilisées en optique pour différentes applications, bien que peut-être la plus connue est de corriger les défauts de vue. Ainsi, ils sont indiqués pour traiter.

[TOC]

Caractéristiques

Lentille convergente. Chetvorno [CC0]

Les lentilles convergentes ont une série de fonctionnalités qui les définissent. En tout cas, le plus important est peut-être ce que nous avons déjà avancé dans sa définition. Ainsi, les lentilles convergentes sont caractérisées par le détournement de la mise au point de tout rayon qui les affecte dans une direction parallèle à l'axe principal.

De plus, de manière réciproque, tout rayon incident qui passe la focalisation est réfracté parallèle à l'axe optique de l'objectif.

Éléments de lentilles convergentes

Face à votre étude, il est important de savoir quels éléments constituent les lentilles en général et les lentilles convergentes en particulier.

En général, il s'appelle le centre optique d'un objectif au point que chaque rayon qui le traverse ne ressent aucune déviation.

L'axe principal est la ligne qui rejoint le centre optique et l'objectif principal, que nous avons déjà commenté qui est représenté avec la lettre F.

Peut vous servir: ton: transformations, équivalences et exercices résolus

Il est appelé l'objectif principal au point où tous les rayons qui affectent l'objectif parallèle à l'axe principal sont trouvés.

La distance entre le centre optique et la focus est appelée distance focale.

Les centres de courbure sont définis comme les centres des sphères qui créent l'objectif; étant, en revanche, les radios de courbure les radios des sphères qui donnent naissance à l'objectif.

Et enfin, il est appelé plan optique vers le plan central de l'objectif.

Formation d'images dans des lentilles convergentes

Face à la formation d'images dans des lentilles convergentes, une série de règles de base expliquées ci-dessous doit être prise en compte.

Si le rayon affecte l'objectif parallèle à l'axe, le rayon émergent converge dans l'image de mise au point. Inversement, si un rayon incident traverse la mise au point de l'objet, la foudre émerge dans une direction parallèle à l'axe. Enfin, les rayons qui traversent le centre optique sont réfractés sans subir de déviation.

En conséquence, dans une lentille convergente, vous pouvez donner les situations suivantes:

- Que l'objet est situé par rapport au plan optique à une distance supérieure à la double de la distance focale. Dans ce cas, l'image qui se produit est réelle, inversée et plus petite que l'objet.

- Que l'objet est situé à une distance du plan optique égal à deux fois la distance focale. Lorsque cela se produit, l'image obtenue est une image réelle et inversée et de la même taille que l'objet.

- Que l'objet est à une distance du plan optique entre une et deux fois la distance focale. Ainsi, une image est produite est réelle, inversée et plus grande que l'objet d'origine.

- Que l'objet est situé à une distance du plan optique inférieur à la distance focale. Dans ce cas, l'image sera virtuelle, directe et plus grande que l'objet.

Peut vous servir: choc magnétique: unités, formules, calcul, exemples

Types d'objectifs convergents

Il existe trois types différents de lentilles convergentes: les objectifs biconvexes, les objectifs planoconvexes et les objectifs concavoconvexes.

Les objectifs biconvexes, comme son nom l'indique, sont composés de deux surfaces convexes. Les planoconvexas, quant à eux, ont une surface plane et un autre convexe. Et enfin, les lentilles concavoconvexes sont constituées d'une surface légèrement concave et d'un autre convexe.

Différence avec les lentilles divergentes

Lentille convergente. Fir0002 (talk) (téléchargement) [CC BY-SA 3.0 (http: // CreativeCommons.Org / licences / by-sa / 3.0 /]]

Les lentilles divergentes, en revanche, diffèrent du convergent en ce que l'épaisseur diminue des bords vers le centre. Ainsi, contrairement à ce qui s'est passé avec le convergent, dans ce type de lentilles, les rayons de lumière qui affectent l'axe principal en parallèle. De cette façon, ils forment ce qu'on appelle des images virtuelles d'objets.

En optique, les objectifs divergents ou négatifs, comme ils sont également connus, sont principalement utilisés pour corriger la myopie.

Équations Gauss des lentilles minces et lentilles accrues

En général, le type de lentilles étudiées sont celles appelées lentilles minces. Ceux-ci sont définis comme ceux qui ont une petite épaisseur par rapport à la courbure des surfaces qui les limitent.

Ce type d'objectif peut être étudié avec l'équation de Gauss et avec l'équation qui permet de déterminer l'augmentation d'une lentille.

Équation de Gauss

L'équation Gauss des objectifs minces sert à résoudre la multitude de problèmes d'optique de base. D'où sa grande importance. Votre expression est la suivante:

1 / f = 1 / p + 1 / q

Où 1 / f est ce qu'on appelle la puissance d'un objectif et f est la distance focale ou la distance du centre optique au focam. L'unité de mesure de la puissance d'une lentille est la dioptre (d), étant 1 d = 1 m^-1. De sa part, P et Q sont respectivement la distance à laquelle un objet et la distance à laquelle son image est observée.

Il peut vous servir: Théorie du Big Bang: caractéristiques, étapes, preuves, problèmes

Augmentation de la lentille

L'augmentation latérale d'une crise mince est obtenue avec l'expression suivante:

M = - Q / P

Où m est l'augmentation. D'après la valeur de l'augmentation, une série de conséquences peut être déduite:

Oui | M | > 1, la taille de l'image est supérieure à celle de l'objet

Oui | M | < 1, el tamaño de la imagen es menor que el del objeto

Si m> 0, l'image est correcte et du même côté de l'objectif que l'objet (image virtuelle)

Oui m < 0, la imagen está invertida y en el lado contrario que el objeto (imagen real)

Exercice résolu

Un corps est situé à un mètre d'un objectif convergent, qui a une distance focale de 0, 5 mètres. À quoi ressemblera l'image du corps? Jusqu'où allez-vous trouver?

Nous avons les données suivantes: p = 1 m; F = 0,5 m.

Nous remplaçons ces valeurs dans l'équation de Gauss des lentilles minces:

1 / f = 1 / p + 1 / q

Et les restes suivants:

1 / 0,5 = 1 + 1 / q; 2 = 1 + 1 / q

Nous effacons 1 / q

1 / q = 1

Pour ensuite effacer Q et obtenir:

Q = 1

De là, nous remplaçons dans l'équation de l'augmentation d'une lentille:

M = -Q / P = -1 / 1 = -1

Par conséquent, l'image est réelle depuis Q> 0, inversée car m < 0 y de igual tamaño dado que el valor absoluto de M es 1. Por último, la imagen se encuentra a un metro de distancia del foco.

Les références

1. Lumière (n.d.). À Wikipedia. Récupéré le 18 mars 2019.Wikipédia.org.
2. Lekner, John (1987). Théorie de la réflexion, des vagues électromagnétiques et de la pune. Springer.
3. Lumière (n.d.). À Wikipedia. Récupéré le 20 mars 2019 de.Wikipédia.org.
4. Lens (n.d.). À Wikipedia. Récupéré le 17 mars 2019.Wikipédia.org.
5. Lens (optique). À Wikipedia. Récupéré le 19 mars 2019 de.Wikipédia.org.
6. Actes, Eugene (2002). Optique (4e ed.). Addison Wesley.
7. Tupler, Paul Allen (1994). Physique. 3e édition. Barcelone: ​​J'ai inversé.