Côtés homologues

Nous expliquons ce que sont les côtés homologues, avec des exemples et des exercices résolus

Que sont les côtés homologues?

Les côtés homologues En deux figures géométriques plates sont celles qui correspondent les unes aux autres, en gardant la similitude. Par exemple, la main droite d'une personne est homologue avec la main droite d'une autre personne.

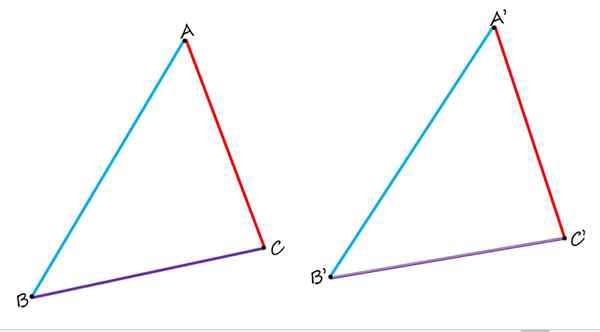
En géométrie plate, il n'y a pas seulement des côtés homologues, mais aussi des sommets et des angles homologues. Pour le voir, considérez la figure suivante, qui se compose de deux triangles identiques ABC et A'B'C ':

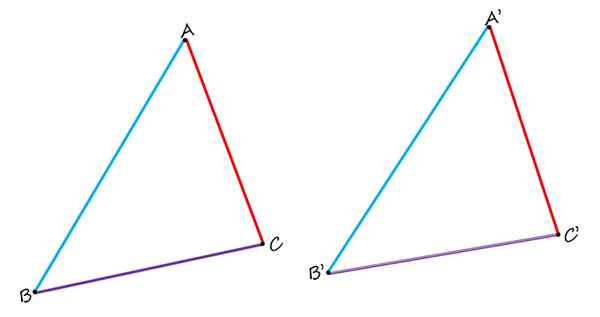Dans les deux triangles identiques montrés, l'AB et A'B ', sont homologues, ainsi que les côtés BC et B'C' et AC et A'C '. Source: F. Zapata.

Lorsque vous les comparez, il est clairement observé que les côtés ab et a'b 'en bleu sont homologues, car ils occupent une position similaire dans chaque triangle. Les côtés BC et B'C 'en violet sont également homologues. Et enfin, le côté AC rouge est homologue du côté a'c '.

Explication

D'après les prévisions susmentionnées, il s'ensuit que les côtés homologues sont ceux qui occupent la même position relative dans les chiffres de la même manière. Dans l'image précédente, deux triangles identiques ont été utilisés pour montrer l'idée, mais cela peut facilement généraliser d'autres figures géométriques plates, formées par des côtés consécutifs qui ferment.

Ces chiffres sont appelés polygones. Par exemple, les triangles et les quadrilatéraux sont respectivement des polygones de 3 et 4 côtés.

Le concept de côtés homologues est important car il permet de définir des critères de similitude entre les polygones, comme on le verra sous peu. Les chiffres similaires ont exactement la même forme et conservent une proportion identique entre leurs côtés, même s'ils ne sont pas de la même taille.

Et bien que jusqu'à présent, la référence ait été faite uniquement à des chiffres plats, il existe également des chiffres similaires en trois dimensions. Ils sont facilement observés dans les étagères des supermarchés, lorsque le même produit est vendu dans des conteneurs identiques, mais avec une taille différente.

Peut vous servir: logique mathématique

D'autres mots utilisés de manière interchangeable en géométrie pour désigner les côtés homologues sur les figures géométriques sont: les côtés correspondants, les côtés respectifs et les côtés équivalents.

Sommets et angles homologues

Comme pour les côtés, les sommets homologues sont également définis, qui unissent des paires de côtés homologues. Par exemple, les sommets A et 'de la figure précédente sont homologues. De même, les paires de sommets B et B 'et C et C' sont homologues.

Enfin, les angles homologues occupent la même position relative dans les chiffres. Les sommets des angles homologues sont à leur tour homologues.

Pour illustrer l'idée, prenez l'angle entre les côtés bleus et violets du triangle gauche, qui peut être indiqué comme ∠ABC. Cet angle a son homologue à l'angle ∠a'b'c ', du triangle à droite.

Le sommet de cet angle est B, qui comme indiqué précédemment, est un homologue avec B ', et les deux autres paires d'angles homologues des triangles montrés sont:

• ∠bca et ∠b'c'a '
• ∠cab et ∠c'a'b '

Similitude des polygones

Pour que deux polygones soient similaires, les conditions suivantes doivent être remplies:

• Toutes les paires d'angles homologues ont la même mesure
• Ses paires de côtés homologues sont proportionnelles.

Les deux conditions doivent être remplies simultanément pour assurer la similitude. On observe immédiatement pourquoi.

Dans la figure suivante, il y a deux quadrilatères qui ne sont évidemment pas similaires. Cela est dû au fait que le premier statut de chaque semaine est rempli, mais le second ne le fait pas:

Deux quadrilatères qui ne sont pas similaires, bien que leurs angles homologues aient une mesure égale. Source: F. Zapata.

Alors que dans les chiffres, leurs paires d'angles homologues ont la même mesure, car tous sont des angles droits (ils mesurent 90º), les chiffres ne sont pas similaires, car leurs paires de côtés ne sont pas proportionnelles.

Peut vous servir: fonction injective: de quoi elle consiste, à quoi sert-elle et des exemples

D'un autre côté, ces deux quadrilatères ont des côtés homologues avec une même mesure, mais les angles homologues ne mesurent pas la même. Par conséquent, les chiffres ne sont clairement pas similaires.

Deux quadrilatères avec des côtés homologues de la même mesure, mais avec des angles internes différents, ce ne sont donc pas des chiffres similaires. Source: F. Zapata.

Raison de similitude

Si deux chiffres sont similaires, le quotient entre les côtés homologues est le même et est appelé Raison de similitude.

Dénotant les côtés de l'une des figures telles que A, B, C, D ... et celles correspondantes de l'autre figure comme a ', b', c ', d

Périmètres et zones de chiffres similaires

Le rapport de similitude permet d'obtenir des relations entre les périmètres, les zones et les volumes de deux chiffres similaires.

Raison périmètre de deux chiffres similaires

Le périmètre P d'un polygone est défini comme la somme de tous ses côtés. Si vous avez un chiffre dont les côtés sont un ', b', c ', d' ..., son périmètre p 'est:

P '= a' + b '+ c' + d '.. .

Si un autre polygone est similaire à cela et que ses côtés sont a, b, c, d ..., il est accompli que:

Et par conséquent:

A = r ∙ a '

Vous pouvez affirmer la même chose pour les autres côtés de cette figure. Ainsi, le périmètre P est exprimé comme:

P = a + b + c + d .. . = r ∙ a '+ r ∙ b' + r ∙ c '+ r ∙ d' +…

Étant donné que "R" est un facteur commun pour tous les toxicomanes, la relation entre P et P 'est:

P = r ∙ p '

Cela signifie que la raison des périmètres entre deux polygones similaires est égal à la raison de la similitude.

Raison des zones de deux chiffres similaires

Si deux chiffres similaires ont respectivement des zones A et A ', celles-ci sont liées à travers:

Peut vous servir: exercices de dégagement de la formule

A = r²∙ A '

Où "r" est la raison de la similitude des chiffres.

Ratio de volume de deux chiffres similaires

Ce sont deux figures similaires à trois dimensions, dont les volumes sont respectivement, V et V '. La relation entre eux, à travers "r" est:

V = r³∙ v '

Exemples

Plans

Des parties d'un terrain, la plante d'un immeuble ou même d'un vêtement, à plus petite échelle sur une feuille de papier peut être représentée. Les plans ont l'avantage de pouvoir emporter avec eux et de faciliter les modifications pertinentes, avant de mettre en pratique l'objet réel.

Plans

Ce sont généralement des représentations dans le plan d'une grande zone de terrain, d'un village aux continents. Ils sont également fabriqués à une certaine échelle.

Ils ont de nombreuses applications et il existe de nombreux types. Par exemple, à travers une carte, le terrain peut être décrit, et lorsqu'il est situé sur un point spécifique, le meilleur itinéraire pour passer de ce point à un autre est déterminé.

Des modèles

Ce sont des représentations à trois dimensions à l'échelle d'objets tels que les voitures, les bâtiments et les constructions en général.

Exercice résolu

Les valeurs suivantes correspondent aux côtés de quelques triangles similaires. Trouvez la raison de la similitude et des valeurs de "x" et "y":

Triangle 1: 5, 8, 10

Triangle 2: 150, x, y

Solution

La raison de la similitude est le quotient:

R = 150/5 = 30

Donc:

x = 30 × 8 = 240

y = 10 × 30 = 300