Égalité mathématique

Figure 1.- L'égalité mathématique garantit que 1 + 1 est le même 2

Qu'est-ce que l'égalité mathématique?

Une égalité mathématique garantit que deux expressions sont identiques ou différentes, elles sont totalement équivalentes. Ces expressions peuvent être une nature diversifiée, par exemple des nombres, des lettres qui symbolisent des quantités ou des amplitudes, des combinaisons de nombres et de lettres, de matrices et plus.

Le symbole utilisé pour désigner l'égalité dans le langage mathématique est celui de deux lignes parallèles et horizontales, qui dans le texte imprimé est le symbole bien connu "=". Par exemple, si vous avez trois pommes, vous pouvez écrire l'égalité suivante:

Nombre de pommes = 3

L'expression «nombre de pommes» est le membre de la gauche et le numéro 3 est le membre à droite de l'égalité.

Comme il est possible d'écrire des quantités numériques de différentes manières, l'égalité est utilisée pour les désigner. Prenant un cas spécifique pour illustrer le point, il existe plusieurs façons d'écrire le numéro 4, à part les plus évidents de 4 = 4, les éléments suivants peuvent être écrits, par une égalité mathématique:

2 + 2 = 4
6 - 2 = 4
8 ÷ 2 = 4
2 × 2 = 4
2² = 4

L'égalité montrée ici est vraie, mais une égalité peut ne pas l'être, par exemple 10 + 5 = 20, est fausse, puisque 10 + 5 = 15.

Le lecteur connaît sûrement d'autres façons d'écrire le numéro 4. Notez que les expressions de chaque côté de l'égalité peuvent être des nombres, des mots, des lettres qui symbolisent des quantités ou d'autres symboles, par exemple:

x + 1 = 7
pour²B - 1 = xy
f (x) = 2x²

Les mathématiciens n'ont pas toujours utilisé le symbole d'égalité, donc les anciens traités en mathématiques étaient très étendus.

Il est attribué au mathématicien et au docteur Robert Remember (1510-1558), né au Pays de Galles, à la création du symbole d'égalité "=", si familier à tous aujourd'hui. Rappelez-vous, apparemment fatigué d'écrire à tout moment, la phrase "comme" dans l'un de ses traités en mathématiques, il a décidé d'abréger à sa place les rayures parallèles des proches.

Peut vous servir: prisme pentagonal: caractéristiques, parties, sommets, bords, volume

Propriétés de l'égalité mathématique

Les propriétés suivantes permettent de travailler correctement avec l'égalité mathématique. Ils sont axiomatiques, donc ils ne nécessitent pas de démonstration:

1.- Propriété réfléchissante

Cette propriété établit que tout montant est égal à lui-même. En particulier, comme n'importe quel nombre est égal à lui-même, les égaux peuvent être écrits:

5 = 5

36.35 = 36.35

Si un montant est littéral ou c'est une combinaison de lettres et de nombres, elle est également égale à elle-même:

3x = 3x

pour²avant JC^-1 = A²avant JC^-1

2.- Propriété de symétrie

Les montants ou les membres des deux côtés de l'égalité peuvent être échangés sans validité perdue. Autrement dit, si ce qui est à gauche du symbole "=" est écrit à votre droite, et ce qui est à votre droite est placé à gauche, c'est la même égalité.

Par exemple, l'expression 5 + 2 = 7 est équivalente à celle: 7 = 5 + 2. De la même manière:

12 + 8 = 20; 20 = 12 + 8

x + 1 = 3; 3 = x + 1

x - z = y; y = x - z

3.- Propriété transitive

Cette propriété fait référence à l'équivalence de l'égalité. Si deux égalités ont un membre commun, alors ils sont également les mêmes, car en général:

Si «x = y» et «y = z» alors x = z

Pour illustrer cette propriété, considérez ces deux égalités numériques: 2 + 2 = 4 et 6 - 2 = 4. Étant donné que les deux sont égaux à 4 (ils ont un membre commun), alors les éléments suivants peuvent être écrits, sans perdre de validité:

2 + 2 = 6 - 2

Un autre exemple, cette fois avec des lettres:

Oui x + 1 = 5

ET

A - b = 5

Ensuite:

x + 1 = a - b

4.- Propriété d'annulation

Une égalité n'est pas modifiée si dans les deux membres, il y a le même montant qui ajoute (ou soustrait) et qu'il est décidé d'éliminer ou d'annuler cela. C'est la propriété d'annulation de la somme.

Prenez comme exemple l'égalité numérique suivante dans laquelle les 10 apparaissent à la fois dans le membre de la droite et dans celui de gauche:

Il peut vous servir: fonctions trigonométriques: basique, dans le plan cartésien, exemples, exercice

2 + 2 + 10 = 6 - 2 + 10

Le numéro 10 peut être annulé sans que l'égalité perde sa validité, laissant une autre égalité plus courte et équivalente à la précédente:

2 + 2 = 6 - 2

En égalité (10 ÷ 2) - 3 = 5 - 3 L'entier - 3 appartient aux deux membres de l'égalité et apparaît comme en ajoutant, donc peut être annulé, obtenant:

10 ÷ 2 = 5

Cela se produit également avec des quantités littérales, par exemple:

Oui x + 2y + z = −a + b + z

Ensuite, le "Z" peut être annulé, car il se trouve des deux côtés de l'égalité comme l'ajout (et avec le même signe).

Ce faisant, il en résulte:

x + 2y = −a + b

Il peut également définir la propriété d'annulation de la multiplication. Si le même montant C multiplie les deux membres de l'égalité, ce montant peut être annulé, par exemple:

Cx = cy

Ensuite, C peut être annulé pour obtenir simplement:

x = y

5.- Propriété d'uniformité

Une égalité reste invariable en ajoutant, en soustrayant, en multipliant ou en se divisant par la même quantité des deux côtés.

Par exemple, il a 8 + 5 = 13, si les deux membres se multiplient par un certain nombre arbitraire C = 2, l'égalité reste:

(8 + 5) × 2 = 13 × 2

13 × 2 = 26

Classes égales mathématiques

Il existe différents types d'égalité mathématique, ils sont donc classés pour leur meilleure compréhension dans:

-Identités, Ils sont l'égalité dans lesquels les deux membres sont identiques:

2 = 2
x = x
2x = x + x

et ainsi de suite.

-Équations, Ce sont des égalités dans lesquelles une ou plusieurs inconnues apparaissent, et sont vraies pour certaines valeurs, c'est-à-dire que l'égalité n'est pas respectée pour une valeur arbitraire, donc elles sont également connues égalités conditionnelles. Exemples:

x + 1 = 5

X³ = 27

A + B = 40

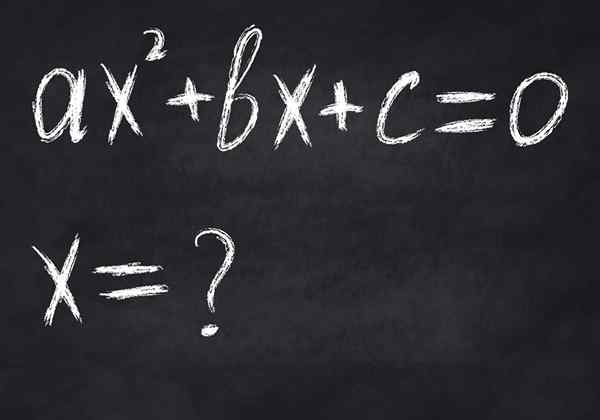Figure 2.- Une équation est une égalité mathématique conditionnelle, car elle n'est respectée que pour certaines valeurs variables. L'image montre une équation au deuxième degré, qui a au plus deux solutions réelles

-Équivalence, En eux, le membre de la gauche est équivalent à celui de droite, même s'ils ne sont pas égaux, par exemple dans: 2³ = 8.

Peut vous servir: principe additif

-Formules, C'est une égalité qui est toujours remplie pour les valeurs de la variable indépendante, comme dans la formule bien connue pour la distance d en fonction du temps t d'un mobile avec un mouvement rectiligne uniforme: D = v ∙ t

Exercices résolus

Exercice 1

Écrivez le numéro 10 à quatre égalités différentes et équivalentes.

Solution

Toutes ces égalités expriment le numéro 10, mais de différentes manières:

5 × 2 = 10

11-1 = 10

dix¹= 10

20 ÷ 2 = 10

Exercice 2

Quelle est la valeur de x qui satisfait l'égalité x + 1 = 3?

Solution

Cette égalité est une équation, car la valeur de x est inconnue. En utilisant la propriété 5, si l'expression x + 1 = 3 est ajoutée (−1) des deux côtés du symbole "=", l'égalité reste:

x + 1 + (−1) = 3 + (- 1)

Lors de l'ajout (−1) au membre de la gauche et l'opération est résolue, le "X" est seul sur le côté gauche de l'égalité, cette procédure est appelée autorisation:

x + 1 - 1 = 3−1

x = 2

Par conséquent, la valeur qui satisfait cette égalité est x = 2.

Exercice 3

Si un mobile avec un mouvement rectiligne uniforme a une vitesse de 2.5 m / s, quelle est la distance qui fonctionne après 3 secondes?

Solution

La formule vue dans la section précédente est utilisée, D = v ∙ t, dans lequel la valeur de v est remplacée:

D = 2.5 ∙ t

L'expression devient une égalité lorsque t = 3 secondes et l'opération est résolue:

D = 2.5 ∙ 3 m = 7.5m

Ce qui se traduit par l'égalité:

D = 7.5m

Les références

1. Barnett, R. 2000. Présculpture. 4e. Édition. McGraw Hill.
2. Larson, R. 2012. Présculpture. 8e. Édition. Cengage Learning.
3. Pérez, V. Propriétés de l'égalité algébrique. Récupéré de: mathématiques.Laguia2000.com.
4. Propriétés de l'égalité. Récupéré de: PPS.K12.Ou.nous.
5. Stewart, J. 2007. Pré-calcul: mathématiques pour le calcul. 5e. Édition. Cengage Learning.