Démonstration des identités pythagoriennes, exemple, exercices

Ils sont Identités pythagoriennes Toutes les équations trigonométriques qui sont remplies pour toute valeur de l'angle et sont basées sur le théorème de Pythagore. L'identité la plus célèbre de pythagore est l'identité trigonométrique fondamentale:

Sen²(α) + cos²(α) = 1

Figure 1. Identités trigonométriques pythagoriennes.

Il est toujours en importance et utilise l'identité pythagorienne de la tangente et du sécateur:

Donc²(α) + 1 = sec²(α)

Et l'identité trigonométrique pythagorienne qui implique la cotangente et la moissonneuse:

1 + ctg²(α) = CSC²(α)

[TOC]

Manifestation

Les raisons trigonométriques sein et cosinus Ils sont représentés dans une circonférence de rayon une (1) connue sous le nom de cercle trigonométrique. Ce cercle a un centre à l'origine des coordonnées ou.

Les angles sont mesurés à partir du semi-axe positif du X, par exemple l'angle α de la figure 2 (voir plus tard). Contrairement aux mains de l'horloge si l'angle est positif, et dans la direction des mains si c'est un angle négatif.

Le semi-droit avec l'origine ou l'angle α est dessiné, qui intercepte le cercle unitaire au point P. Le point P est projeté orthogonalement sur l'axe horizontal x donnant naissance au point C. De même, P est projeté perpendiculairement sur l'axe vertical et donnant lieu au point S.

Vous avez le bon triangle OCP en C. 

Le sein et le cosinus

Il faut se rappeler que la raison trigonométrique sein Il est défini sur un triangle droit comme suit:

Le sein d'un angle du triangle est le rapport ou le rapport entre le cateto opposé à l'angle et l'hypoténuse du triangle.

Appliqué au triangle OCP de la figure 2 serait comme ceci:

Sin (α) = cp / op

Mais cp = os et op = 1, de sorte que:

Sin (α) = os

Ce qui signifie que la projection sur l'axe y a une valeur égale au sein de l'angle indiqué. Il convient de noter que la valeur maximale du sein d'un angle (+1) se produit lorsque α = 90º et le minimum (-1) lorsque α = -90º ou α = 270º.

Peut vous servir: espace vectoriel: base et dimension, axiomes, propriétés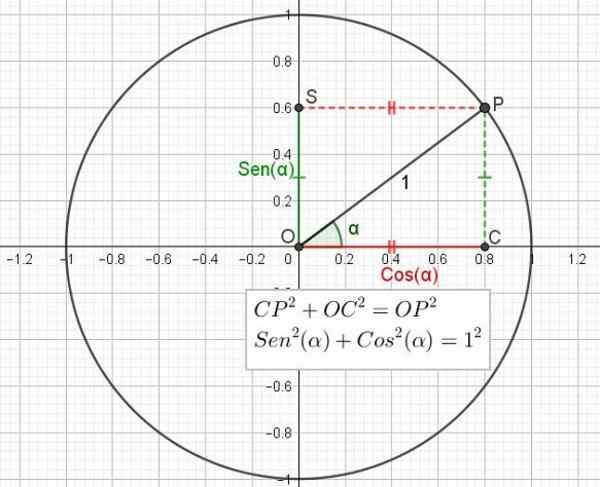Figure 2. Cercle trigonométrique montrant la relation entre le théorème de Pythagore et l'identité trigonométrique fondamentale. (Élaboration propre)

De même, le cosinus d'un angle est le rapport entre la catégorie adjacente à l'angle et à l'hypoténuse du triangle.

Appliqué au triangle OCP de la figure 2 serait comme ceci:

Cos (α) = oc / op

Mais op = 1, donc que:

Cos (α) = OC

Ce qui signifie que la projection OC sur l'axe x a une valeur égale à celle du sein de l'angle indiqué. Il convient de noter que la valeur maximale de la cosinus (+1) se produit lorsque α = 0º ou α = 360º, tandis que la valeur minimale de la cosinus est (-1) lorsque α = 180º.

L'identité fondamentale

Pour le triangle OCP rectangulaire, le théorème de Pythagore est appliqué, qui indique que la somme du carré des catégories est égale au carré de l'hypoténuse:

CP² + OC² = OP²

Mais il a déjà été dit que CP = os = sin (α), que OC = cos (α) et que OP = 1, de sorte que l'expression précédente peut être réécrite en fonction du sinus et du cosinus de l'angle:

Sen²(α) + cos²(α) = 1

L'axe tangent

Tout comme l'axe x dans le cercle trigonométrique est l'axe du cosinus et de l'axe et de l'axe du sein, de la même manière, il y a l'axe de la tangente (voir figure 3) qui est précisément la ligne tangente à l'unité cercle au point au point B coordonnée (1, 0). 

Si vous voulez connaître la valeur de la tangente d'un angle, l'angle est tiré du semi-axe positif du x, l'intersection de l'angle avec l'axe de la tangente définit un point Q, la longueur du segment OQ est la tangente de l'angle.

Peut vous servir: dérivés algébriques

En effet. C'est-à-dire le dire (α) = qb / ob = qb / 1 = qb.

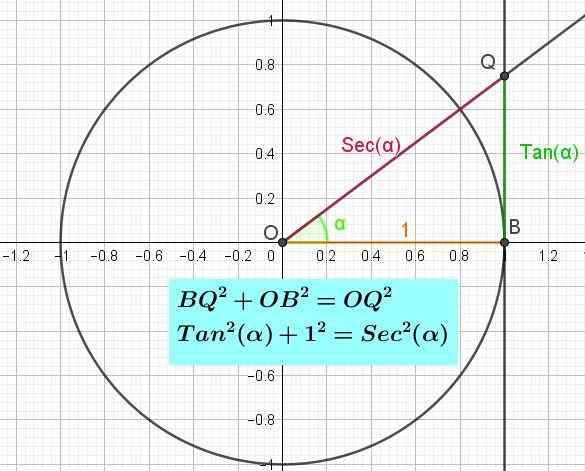figure 3. Le cercle trigonométrique montrant l'axe de la tangente et de l'identité pythagorienne de la tangente. (Élaboration propre)

L'identité pythagorienne de la tangente

L'identité pythagorienne de la tangente peut être démontrée si le triangle rectangle en b (figure 3) est pris en compte (figure 3). Appliquer le théorème de Pythagore audit triangle, vous devez BQ² + Ob² = OQ². Mais il a déjà été dit que bq = tan (α), que ob = 1 et que oq = sec (α), de sorte que le remplacement de l'égalité de pythagore pour le bon triangle obq il a:

Donc²(α) + 1 = sec²(α).

Exemple

Vérifiez si les identités pythagoriennes sont respectées ou non dans le triangle rectangle de Catetos AB = 4 et BC = 3.

Solution: les catégories sont connues, il est nécessaire de déterminer l'hypoténuse, qui est:

Ac = √ (ab ^ 2 + bc ^ 2) = √ (4 ^ 2 + 3 ^ 2) = √ (16 + 9) = √ (25) = 5.

L'angle ∡bac sera appelé α, ∡bac = α. Maintenant, les raisons trigonométriques sont déterminées:

Sin α = bc / ac = 3/5 

Cos α = ab / ac = 4/5 

Tan α = BC / AB = 3/4 

Cotan α = ab / bc = 4/3 

Sec α = AC / AB = 5/4 

CSC α = AC / BC = 5/3

Il commence par l'identité trigonométrique fondamentale:

Sen²(α) + cos²(α) = 1

(3/5) ^ 2 + (4/5) ^ 2 = 9/25 + 16/25 = (9 +16) / 25 = 25/25 = 1

Il est conclu qu'il est accompli.

- La prochaine identité pythagorienne est celle de la tangente:

Donc²(α) + 1 = sec²(α)

(3/4) ^ 2 + 1 = 9/16 + 16/16 = (9 + 16) / 16 = 25/16 = (5/4) ^ 2

Et il est conclu que l'identité de la tangente est vérifiée.

- De même celle de la cotangente:

Peut vous servir: sélections aléatoires avec ou sans remplacement

1 + ctg²(α) = CSC²(α)

1+ (4/3) ^ 2 = 1 + 16/9 = 25/9 = (5/3) ^ 2

Il est conclu qu'il est également rempli, ce qui a terminé la tâche de vérifier les identités pythagoriennes pour le triangle donné.

Exercices résolus

Testez les identités suivantes, en fonction des définitions des raisons trigonométriques et des identités pytagoriques.

Exercice 1

Prouver ce que² x = (1 + sen x) (1 - sin x).

Solution: Le bon membre reconnaît le produit notable de la multiplication d'un binôme par son conjugué qui, comme on le sait, est une différence de carrés:

Cos² x = 1² - Sen² X

Ensuite, le terme avec le sein sur le côté droit passe sur le côté gauche avec le signe modifié:

Cos² X + Sen² x = 1

Notant que l'identité trigonométrique fondamentale a été atteinte, il est donc conclu que l'expression donnée est une identité, c'est-à-dire qu'elle est remplie pour toute valeur de x.

Exercice 2

À partir de l'identité trigonométrique fondamentale et en utilisant les définitions des raisons trigonométriques pour démontrer l'identité pythagoreuse de la moissonneuse.

Solution: l'identité fondamentale est:

Sen²(x) + cos²(x) = 1

Les deux membres sont divisés entre SEN²(x) et le dénominateur est distribué dans le premier membre:

Sen²(x) / péché²(x) + cos²(x) / péché²(x) = 1 / sen²(X)

Il est simplifié:

1 + (cos (x) / sen (x)) ^ 2 = (1 / sin (x)) ^ 2

Cos (x) / sin (x) = cotan (x) est une identité (non-pythagorienne) qui est vérifiée par la définition des raisons trigonométriques. De la même manière, il se produit avec l'identité suivante: 1 / sin (x) = csc (x).

Enfin vous devez:

1 + ctg²(x) = csc²(X)

Les références

1. Baldor J. (1973). Géométrie plate et espace avec une introduction à la trigonométrie. Culturel d'Amérique centrale. C.POUR.
2. C. ET. POUR. (2003). Éléments de géométrie: avec des exercices et une géométrie de la boussole. Université de Medellin.
3. Campos, F., Cerecedo, f. J. (2014). Mathématiques 2. Groupe éditorial de Patria.
4. Iger. (s.F.). Mathématiques Premier semestre Tacaná. Iger.
5. JR. Géométrie. (2014). Polygones. Lulu Press, Inc.
6. Miller, Heeren et Hornsby. (2006). Mathématiques: raisonnement et applications (dixième édition). Pearson Education.
7. Patiño, m. (2006). Mathématiques 5. Progreso éditorial.
8. Wikipédia. Identités et formules de trigonométrie. Récupéré de: est.Wikipédia.com