Histoire de la trigonométrie de ses origines

La Histoire de la trigonométrie Il fait référence à l'ensemble des faits et avancées qui se sont produits autour de cette branche des mathématiques de ses origines aux événements les plus récents.

Lorsque vous faites un bref voyage à travers son histoire, il est évident que cette science est née en réponse aux problèmes rencontrés par les anciens astronomes et navigateurs pour analyser le déplacement des étoiles dans le ciel.

Le terme apparaît pour la première fois dans le livre Trigonometriae Libri Quinque, écrit par le mathématicien et scientifique allemand Pitiscus Bartolomé (1561-1613). Via Wikimedia Commons.

De même, le mot trigonométrie découle de la composition de deux mots grecs: Trigonon (triangle) et Métron (étendue). Le terme apparaît pour la première fois dans le livre Trigonométriae bibri quinque, Écrit par le mathématicien et scientifique allemand Pitiscus Bartolomé (1561-1613).

De cette façon, l'étymologie du mot montre que la trigonométrie est l'étude les relations entre les angles d'un triangle et les segments ou les lignes qui le forment.

[TOC]

Les débuts de la trigonométrie

Les premières étapes de la trigonométrie ont été réalisées par l'homme lorsqu'ils ont été promus par la nécessité de connaître et d'analyser le mouvement des étoiles.

C'est-à-dire que l'être humain a conçu la trigonométrie parce qu'elle a été trouvée dans des situations où il était impossible de faire des mesures directement, car pour calculer les étoiles, des outils mathématiques plus complexes étaient nécessaires.

- Études à Babylone

Table de boue écrite par celles des Babyloniens appelés Plimpton 322. Via: Wikimedia Commons

Des études montrent qu'il y a plus de 3.000 ans Les Babyloniens ont déjà géré le concept d'angle et de raisons trigonométriques, c'est-à-dire qu'ils ont pu établir les relations entre les côtés et les angles des triangles.

Par exemple, une table de boue - écrite par celles des Babyloniens - appelés Plimpton 322 (1800 A. C.) montre une succession de colonnes et de lignes qui contiennent des nombres dans l'écriture cunéiforme. Selon la recherche effectuée par certains experts, cette tablette représente ce qui semble être une série de fonctions trigonométriques.

Peut vous servir: quelle est la directive? (Géométrie)

Les Babyloniens connaissaient les concepts qui ont donné naissance au théorème de Pythagore (569-474 A.C) et ils ont compris leur principe.

De la même manière, ils connaissaient également le théorème attribué à Thales de Miletus (695-546 à.C), qui indique que chaque droit, tracé parallèle sur le côté d'un triangle, forme avec les deux autres côtés un autre triangle qui est similaire au triangle initial.

- Les anciens Égyptiens

Les anciens Égyptiens ont réussi à maintenir la pente uniformément sur chacun des visages pyramidaux. Via: pixabay

Bien qu'il ne soit pas approprié de parler de trigonométrie dans la sphère générale des mathématiques égyptiennes, il ne fait aucun doute que cette civilisation a géré certains concepts trigonométriques.

Cela se produit parce que lorsque vous envisagez les grands bâtiments fabriqués par les Égyptiens, comme les pyramides, on peut conclure qu'ils avaient une certaine connaissance de la trigonométrie.

Une difficulté d'ingénierie de base rencontrée par les Égyptiens - et cela a résolu incroyable.

Pour cela, ils ont utilisé un concept qu'ils ont appelé "Seqt" et cela équivaut à ce que nous comprenons aujourd'hui comme une pente d'une surface plate inclinée.

De plus, les Égyptiens pour effectuer des mesures sur les surfaces verticales utilisées comme unité le "coude" et en horizontal la "main", qui correspondait à 1/7 du coude. De cette façon, ils ont calculé le seqt ou en attente dans les différents bâtiments. Par exemple, dans la pyramide de Jufú (Queope), le seqt est de 5 1/2 mains par coude.

- La Grèce antique et la table à cordes

Toutes les connaissances des Babyloniens et des anciens Égyptiens sont passés en Grèce, où le mathématicien et astronome de Nicaa (190-120 a été mis en évidence (190-120. C), qui est considéré comme le père de la trigonométrie. Hiparco a créé les tables «Strings» avec lesquelles il a réussi à résoudre les problèmes des triangles plats.

NICEA HIPARCO - SOURCE: Transféré de.Wikipedia à Commons par Maksim - dans le domaine public

Pour les faire, il a utilisé une circonférence avec un certain rayon (un rayon est la distance entre le centre d'un cercle et tout point de circonférence).

Peut vous servir: Probabilité conditionnelle: formule et équations, propriétés, exemples

Ensuite, il déplaçait le rayon pour définir différents angles; En faisant cela, il pointait dans le tableau la longueur de la ligne qui était délimitée sur les côtés de l'angle et de la circonférence.

Ces «cordes» se sont avérées être les précurseurs des tableaux des fonctions trigonométriques que nous utilisons aujourd'hui.

- Contributions de l'Inde

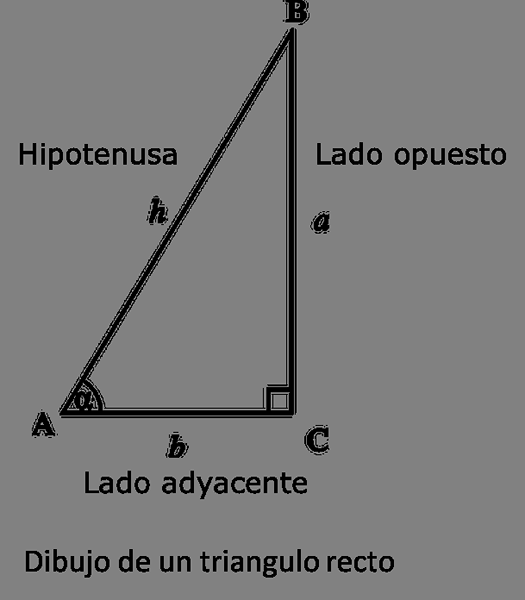Dessin d'un triangle droit.

Comme les chercheurs en Grèce, les astronomes de l'Inde ont également développé un système trigonométrique, mais contrairement aux Grecs, ces astronomes ont basé leur analyse sur la fonction "sinus" au lieu d'utiliser les cordes.

Cependant, la fonction "sinusoïdale" exprimée par ces astronomes n'est pas celle utilisée aujourd'hui; Cette fonction n'était pas une proportion (comme utilisée aujourd'hui), mais la longueur du côté opposé à un angle d'un triangle rectangle dont l'hypoténuse est connue.

- Arabie et fonctions trigonométriques

À la fin du VIIIe siècle, les astronomes arabes, influencés par des études de trigonométrie menées par les peuples de la Grèce et de l'Inde, ont commencé des études importantes sur les relations entre les angles et leurs côtés.

De cette façon, à la fin du 10ème siècle, ils ont soulevé les fonctions bien connues du sein, du cosinus, de la tangente, de la cotangente, du séchage et de la moissonneuse.

Ils ont également découvert et vérifié les théorèmes de la trigonométrie primaire, qui sont utilisés dans l'analyse des triangles plats et sphériques. De plus, les mathématiciens arabes ont suggéré l'utilisation d'une valeur ("1") pour la radio (r = 1), qui a donné naissance à des valeurs modernes des fonctions trigonométriques.

- Contributions de l'Occident

Johann Müller connu sous le nom de Regiomontanus (1436-1476). Systématisation et généralisation des méthodes trigonométriques utilisées dans la zone de géométrie. Via: Wikimedia Commons

Les mathématiques de l'Occident, en particulier entre les XIIe et le XVe siècles, ont été fortement influencés par les postulats de la Grèce antique, de l'Inde et des Arabes.

Peut vous servir: chi carré (χ²): distribution, comment il est calculé, exemples

Pendant ce temps, ils étaient décisifs dans le domaine de la trigonométrie - les contributions de Johann Müller, également connu sous le nom de Regiomontanus (1436-1476). Ce mathématicien a réalisé la systématisation et la généralisation des méthodes trigonométriques utilisées dans la zone de géométrie.

Regiomontanus a élaboré et publié un traité qu'il a appelé De triangulis omnimodis libri quinque, qui était composé de cinq livres et d'un total de 131 pages.

Dans ce livre, il a régulé tous les concepts de trigonométrie plate et sphérique, qui ont ensuite été utilisés par d'importants astronomes tels que: Nicolás Copernic.

- Trigonométrie des XVIIe et XVIIIe siècles

Au cours du XVIIe siècle, les études sur les calculs trigonométriques ont prospéré grâce aux contributions de mathématiciens tels que le Scotch John Napier (1550-1617), qui a soulevé diverses méthodes de résolution des triangles sphériques.

John Napier. Source: par Encecard par Samuel Freeman (1773-1857) [Domaine public], via Wikimedia Common

Plus tard, au XVIIIe siècle, les contributions du mathématicien suisse Leonhard Euler (1707-1783) ont été décisives, car ses études ont posé les fondements de la trigonométrie moderne en introduisant la notation actuellement utilisée pour les fonctions trigonométriques.

De plus, Euler a réussi à définir la fonction exponentielle et a découvert sa relation avec les fonctions trigonométriques, ce qui lui a permis de décrire les caractéristiques de la trigonométrie.

Par la suite, Sir Isaac Newton (1643-1727), en inventant le calcul différentiel et intégral, a facilité la représentation d'un grand nombre de fonctions mathématiques, parmi lesquelles sont trigonométriques. De cette façon, la trigonométrie est devenue une partie de l'analyse mathématique, où aujourd'hui joue un rôle fondamental.

Illustration de Sir Isaac Newton

Les références

1. Mansfield, Daniel. Wildberger, n. (2017). Plimpton 322 est la trigonométrie sexageimale exacte babylonienne. Récupéré le 20 mai 2020 de: ScienceDirect.com
2. Jimenez S. (2017). Histoire de la trigonométrie et de ses applications. Récupéré le 23 mai 2020 Deedu
3. Pérez, V. (2010). Histoire de la trigonométrie. Récupéré le 22 mai 2020 de: Laguia2000.com
4. S.POUR. (s.F.) Trigonométrie. Récupéré le 23 mai 2020 de: BlogSpot.com
5. Merlet, Jean-Pierre (2004). Une note sur l'histoire des fonctions trigonométriques. Récupéré le 22 mai 2020 de: net
6. Adamek, t., Penkalski, K., Valentin, G. (2005). L'histoire de la trigonométrie. Récupéré le 23 mai 2020 de: CitSeSerx.It.PSU.Edu /