Matematiques

Hyperbole

3904
1160
Adam Mercier

Qu'est-ce qu'une hyperbole?

L'hyperbole est l'ensemble des points du plan de telle sorte que la valeur absolue de la différence entre les distances à deux points fixes, appelés projecteurs, reste constant. Cet ensemble de points forme la courbe avec deux branches observées sur la figure 1.

Il y a un point P (x, y), les foyers f₁ et f₂ séparé une distance égale à 2C. La façon mathématique d'exprimer cette relation est à travers:

$\left |d__P_1-d__P_2 \right |=constante$

Figure 1. Hyperbole avec axe focal horizontal. Source: F. Zapata.

Tous les points de l'hyperbole satisfont à cette condition, ce qui mène à l'équation d'hyperbole, comme on le verra plus tard. Le point médian entre les projecteurs est appelé centre C et sur la figure, il coïncide avec le point (0,0), mais l'hyperbole peut également être déplacée et son centre correspond à un autre point de coordonnée C (H, K).

Dans la figure supérieure, l'axe x est l'axe focal de l'hyperbole, car il y a les projecteurs, mais vous pouvez également en construire un dont l'axe focal est l'axe et l'axe.

L'hyperbole fait partie des courbes appelées conique, Ils sont appelés ainsi parce qu'ils peuvent être dérivés de la coupe d'un cône avec une section plate. Une hyperbola est obtenue lors de la croisement du cône et du plan, à condition qu'il ne passe pas à travers le sommet du cône et l'angle qui forme le plan avec l'axe du cône est inférieur à celui qui se forme avec l'axe de génératrice de la même.

Avec la parabole, la circonférence et l'ellipse, les coniques sont connues depuis les temps anciens. Le mathématicien grec Apollonius de Perga (262-190 avant JC) a écrit un traité de géométrie où il a détaillé ses propriétés et il leur a lui-même donné les noms avec lesquels ils se connaissent jusqu'à aujourd'hui.

Caractéristiques de l'hyperbole

Ce sont quelques-unes des caractéristiques les plus remarquables d'une hyperbole:

C'est une courbe plate, donc il suffit de donner les coordonnées (x, y) de chaque point qui lui appartient.
C'est aussi une courbe ouverte, contrairement à la circonférence ou à l'ellipse.
Il a deux branches disposées symétriquement.
L'axe vertical et l'axe horizontal peuvent être considérés comme des axes de symétrie, mais l'axe où les projecteurs sont appelés axe focal ou axe principal.
Il est symétrique par rapport à son centre.
L'hyperbole coupe l'axe focal à deux points appelés Sommets, C'est pourquoi l'axe focal est parfois appelé axe réel, tandis que l'autre axe est appelé Axe imaginaire, Parce qu'il n'a aucun point en commun avec l'hyperbole.
Le centre de l'hyperbole est situé à mi-chemin entre les points appelés foyers.
Il est associé à deux lignes très particulières appelées asymptotes, qui sont des lignes auxquelles l'hyperbole s'approche, mais sans les traverser, lorsque les valeurs de x e y sont très grandes. Les asymptotes se croisent au centre de l'hyperbole.

Peut vous servir: fonction sur-objectif: définition, propriétés, exemples

Équations et formules

Équation de hipère avec centre dans (0,0)

À partir de la définition donnée au début:

$\left |d__P_1-d__P_2 \right |=constante$

À cette constante positive, elle est généralement appelée 2a et c'est la distance qui sépare les sommets de l'hyperbole, puis:

$\left |d__P_1-d__P_2 \right |=2a$

D'un autre côté, DP₁, DP₂ et 2c sont les côtés du triangle illustré à la figure 1, et par géométrie élémentaire, la soustraction des carrés des côtés de tout triangle est toujours inférieure au carré du côté restant. Ensuite:

4e²< 4c²

ET:

pour < c

Ce résultat sera utile sous peu.

Comme distance entre deux points p₁(X₁,et₁) Et P₂(X₂,et₂) est:

$d_12=\sqrt(x_2-x_1)^2+(y_2-y_1)^2$

En remplaçant les coordonnées p (x, y), f₁(-C, 0) et f₂(C, 0) Il reste:

$\left |d_P_1-d_P_2 \right |=\left |\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2 \right |=2a$

Ce qui équivaut à:

$\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2=\pm 2a$

Square dans les deux membres pour éliminer les racines et réorganiser les termes que vous atteignez:

$\left (c^2-a^2 \right )x^2-a^2 y^2 =\left (c^2-a^2 \right )a^2$

À la quantité c² - pour², ce qui est toujours un montant positif car < c, se la denomina b², Par conséquent, ce qui précède est réécrit comme:

b²X² - pour²et² = A² b²

Diviser tous les termes par² b², Il s'agit de l'équation d'hyperbola centrée sur (0,0) avec l'axe réel horizontal:

$\fracx^2a^^2-\fracy^2b^^2=1$

Avec a et b supérieur à 0. Cette équation est appelée Hyerbola Canonical Equation et le dénominateur de² Il correspond toujours à la fraction positive.

L'hyperbole centrée sur (0,0) et avec le véritable axe vertical prend la forme:

$\fracy^^2a^2-\fracx^^2b^2=1$ Intersections de l'hyperbole avec les axes de coordonnées

Les intersections de l'hyperbole avec les axes de coordonnées se font respectivement y = 0 et x = 0 dans l'équation:

Pour y = 0

X² /pour² = 1 ⇒ x² = A²

x = ± a

L'hyperbole coupe à l'axe x en deux points appelés sommets, dont les coordonnées respectives x sont: x = a y x = -a

Pour x = 0

Il est obtenu - et² / b² = 1, qui n'a pas de solution réelle et suit que l'hyperbole ne coupe pas à l'axe vertical.

Équation d'hyperbola avec centre en (h, k)

Si le centre de l'hyperbole est au point C (H, K), alors son équation canonique est:

$\frac\left (x-h \right )^2a^^2-\frac\left (y-k \right )^2b^^2=1$

Éléments de hiperbole

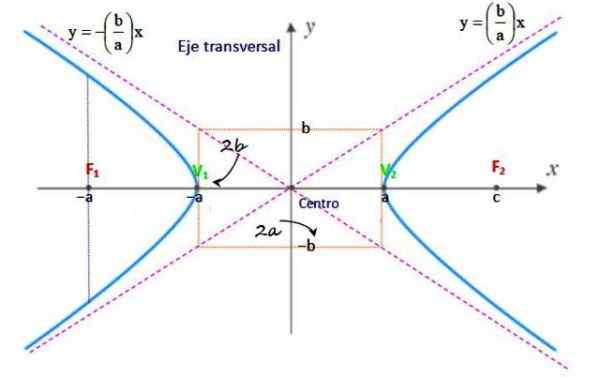Figure 2. Éléments de hiperbole. Source: F. Zapata.

centre

C'est le milieu du segment f₁F₂Et ses coordonnées sont (h, k) ou (x_soit,et_soit).

Peut vous servir: division synthétique

Focos

Ce sont les deux points fixes F₁ et f₂ qui sont sur l'axe réel de l'hyperbole, par rapport à laquelle la différence de distances au point P (x, y) reste constante. La distance entre les projecteurs et le centre de l'hyperbole est "C".

Radio vectorielle

C'est ce qu'on appelle la distance entre un point P et l'un des projecteurs.

Distance focale

C'est la distance qui sépare les deux projecteurs et équivaut à 2C.

Sommets

Les sommets V₁ et V₂ Ce sont les points où l'hyperbole coupe l'axe réel. Un sommet et le centre de l'hyperbole sont séparés par la distance a, par conséquent, la distance entre les sommets est 2A.

Axe focal, axe principal ou axe réel

C'est l'axe où se trouvent les projecteurs et mesure 2C. Il peut être situé sur l'un des deux axes cartésiens et l'hyperbola l'intervient aux points appelés sommets.

Axe transversal, axe secondaire ou axe imaginaire

C'est l'axe perpendiculaire à l'axe focal et mesure 2b. L'hyperbola ne l'interrecte pas, il est donc également appelé axe imaginaire.

Asymptotes

Ce sont deux lignes, dont le respect respectif est m₁ = (b / a) et m₂ = - (b / a), qui sont destinés au centre de l'hyperbole. La courbe n'inscrit jamais ces lignes et le produit entre les distances de tout point de l'hyperbole aux asymptotes, c'est constant.

Pour trouver les équations des asymptotes, faites simplement correspondre le côté gauche de l'équation canonique de l'hyperbole à 0. Par exemple, pour l'hyperbole centrée sur l'origine:

$\fracx^^2a^2-\fracy^^2b^2=0\Rightarrow \fracy^^2b^2=\fracx^^2a^2$

Rectangle d'hyberbola

C'est le rectangle dont la largeur est la distance entre les sommets 2a et la distance 2b et se concentre sur le centre de l'hyperbole. Sa construction facilite la disposition manuelle de l'hyperbole.

Côté droit

Corde qui passe par l'un des projecteurs, perpendiculaire à l'axe réel.

Excentricité

Il est défini comme le quotient entre la distance focale et l'axe réel:

E = c / a

Il est toujours supérieur à 1, car C est supérieur à A, et inférieur à √2.

La valeur et indique si l'hyperbole est plutôt fermée (rectangle étroit, allongée dans le sens de l'axe principal) ou ouvert (large rectangle, allongé dans la direction de l'axe imaginaire).

Tangente droite à l'hyperbole au point P (x₁,et₁)

Une ligne tangente à l'hyperbole à un point P (x₁,et₁) C'est la bissectrice des deux vecteurs de radios de ce point.

Pour une hyperbole avec l'axe principal parallèle à l'axe x, la pente de la ligne tangente à l'hyperbole à un point p (x₁,et₁) est donné par:

Peut vous servir: opérations combinées

$m=\left (\fracba \right )^2\left (\fracx_1y_1 \right )$

Et si l'hyperbole est l'axe principal parallèle à l'axe y, alors:

$m=\left (\fracab \right )^2\left (\fracx_1y_1 \right )$

Exemples d'hyperbole

Dispersion des particules alpha par un noyau

En bombardant les noyaux atomiques avec des particules alpha, qui ne sont que des noyaux d'hélium, ceux-ci sont repoussés, car tout noyau atomique a une charge positive. Ces noyaux d'hélium sont dispersés après des trajectoires hyperboliques.

Trajectoires des corps du système solaire

Figure 3: planètes du système solaire

Dans le système solaire, les objets se déplacent sous l'action de la force de gravité. La description du mouvement découle d'une équation différentielle dans laquelle la force est conservatrice et inversement proportionnelle au carré de la distance. Et les solutions de cette équation sont les trajectoires possibles qui suivent les objets.

Eh bien, ces trajectoires sont toujours coniques: circonférences, ellipses, paraboles ou hyperbolas. Les deux premiers sont des courbes fermées, et c'est ainsi que les planètes se déplacent, mais certaines comètes sont encore des trajectoires ouvertes, comme les paraboles ou les hyperbolas, avec le soleil situé dans l'un des projecteurs.

Son minimum

Lorsqu'il y a deux sources sonores, telles que deux haut-parleurs qui émettent les sons uniformément dans toutes les directions, situées le long d'une ligne droite, les minimums de l'intensité sonore (interférence destructive) se trouvent sur une hyperbole dont l'axe principal est ledit ligne, et sous les projecteurs de Les hyperbola sont les haut-parleurs.

Exercice résolu

Trouvez les éléments de l'hyperbole suivante: sommets, foyers et asymptotes de l'hyperbole et construisez son graphique:

$\fracx^^216-\fracy^^24=1$

Solution

Le centre de cette hyperbole coïncide avec l'origine des coordonnées et son axe réel est horizontal, car la fraction positive correspond à la variable x.

Les semi-axes hyperbola sont:

pour² = 16 ⇒ a = 4

b² = 4 ⇒ b = 2

De cette façon, le rectangle central mesure 4 unités de large et 2 unités de haut. Se souvenant qu'il a été mentionné ci-dessus² - pour²= b², ensuite:

c² = A²+ b² ⇒ C² = 16 + 4 = 20

Par conséquent, le semi-service focal est:

C = √20 = 2√5

Et les foyers sont à des points de coordonnées F₁ (-2√5.0) et f₂ (2√5.0).

Les pentes des asymptotes sont:

m = ± (b / a) = ± (2/4) = ± 0.5

Par conséquent, les équations respectives de chacun sont:

et₁ = 0.5x; et₂ = -0.5x

L'hyperbola peut facilement graphiquement via des logiciels en ligne comme Geogebra:

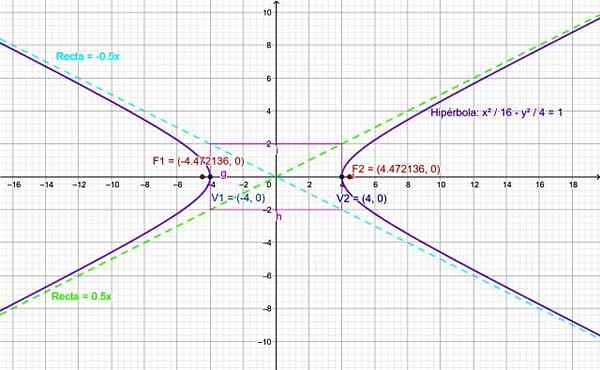Figure 4. Graphique pour l'hyperbole de l'exercice résolu. Source: F. Zapata.

Les références