Heptagone

Un exemple d'heptagone

Qu'est-ce qu'un heptagone?

Il heptagone C'est un polygone avec sept côtés et sept angles internes. En tant que mot géométrique, le mot heptagon provient du grec Hepta, ce qui signifie sept, et Gonos, Traduit par un angle. C'est donc un polygone avec sept angles.

Un polygone est une figure géométrique plate qui forme et fermant trois segments ou plus, également appelés côtés. Les points communs des côtés sont appelés Sommets.

La région entre les côtés adjacents, à l'intérieur de la figure, est le Angle interne, dont le sommet est également l'un des sommets de l'heptagone.

Si tous les côtés et les angles internes ont la même mesure, c'est un heptagone régulier, sinon est un heptagone irrégulier. Les heptons irréguliers adoptent une grande variété de formes.

Un heptagone peut aussi être convexe soit concave, Selon la mesure de ses angles internes. Si les angles internes mesurent moins de 180 °, l'heptagone est convexe, mais si un ou plusieurs desdits angles dépassent 180 °, alors c'est concave.

Un heptagone dont les côtés sont tous de la même mesure Balatéral. Cela peut être concave ou convexe, régulier ou irrégulier.

Heptagone régulier et irrégulier

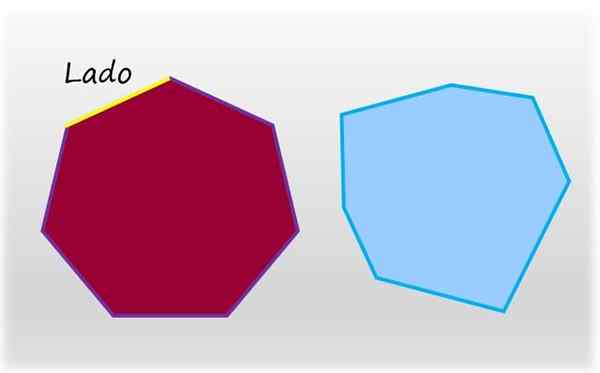L'heptagone est la figure plate et fermée de sept côtés. À gauche, un heptagon ordinaire, dont les côtés et les angles internes ont une mesure égale. À droite, un heptagone irrégulier. Source: F. Zapata.

L'heptagone ordinaire est celui qui a ses sept côtés et ses sept angles internes de mesure égale, l'opposé d'un heptagone irrégulier, qui a au moins un côté d'une mesure différente, ou un angle interne différent.

L'heptagone ordinaire

Symétrie

Un heptagone ordinaire est une figure très symétrique. Des segments peuvent être dessinés qui connectent un sommet au milieu du côté opposé, qui se croisent tous au centre de l'heptagone. Ce sont les sept axes de symétrie sur la figure.

Peut vous servir: zone d'un pentagone régulier et irrégulier: comment il est pris, exerce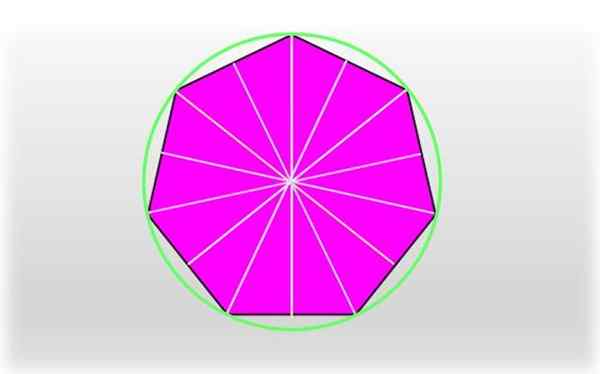 Un heptagone ordinaire et ses axes de symétrie. La circonférence qui passe par chacun des sommets de l'heptagone est appelée circonférence circonscrite.

Le segment qui rejoint un sommet avec le centre de l'heptagone s'appelle Circonnadio, Il correspond au rayon de la circonférence unique qui passe par chacun des sommets, comme le montre la figure.

Angle

Dans l'heptagone, les angles suivants se distinguent:

• Angle interne ϕ, dont le sommet coïncide avec l'un des sommets de l'heptagone, étant les côtés de l'angle, deux des côtés adjacents de l'heptagone. Pour un heptagon ordinaire, la mesure de chacun des sept angles internes est d'environ 128.57 °.
• Angle externe, celui qui se forme entre l'un des côtés et la prolongation de l'un des côtés adjacents, étant le sommet commun entre ces deux côtés le sommet de l'angle. De même, sept angles externes sont formés et leur valeur est calculée en soustrayant 180 ° de l'angle interne, qui pour l'heptagone ordinaire, entraîne 51.43 °.
• Angle central θ, Il a son sommet au centre de l'heptgon ordinaire. Il est calculé en divisant 360 ° par 7, ce qui entraîne environ 51.43 °.

La somme de l'angle interne et de l'angle central est égale à 180 °, c'est-à-dire:

ϕ + θ = π

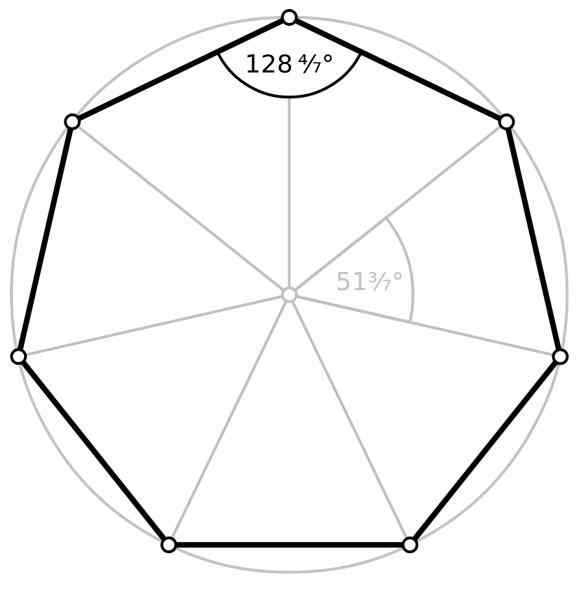Angle interne et angle central de l'heptagone ordinaire. Source: Wikimedia Commons

Zone

Pour l'heptagone ordinaire, il existe des formules, tandis que pour l'heptagone irrégulier, vous devez recourir à d'autres méthodes, telles que la diviser en d'autres polygones plus simples, tels que les triangles.

Il peut vous servir: règle t: caractéristiques, afin que ce soit, des exemples

Zone heptagone ordinaire

1. Si le périmètre P et l'apothéme à_p:

Que ce soit dans la région de l'heptagone. Il existe une formule pour calculer la zone, valide pour tout polygone ordinaire:

2. Si les L et l'apothem sont connus pour_p:

Puisque le périmètre est la somme des côtés et que le côté mesure L dans l'heptagone ordinaire, il est obtenu:

P = 7⋅l

Remplacement dans la formule précédente:

3. Si le côté est connu        

Ce qui suit est une formule approximative et valide lorsque la mesure de l'heptagone est connue:

A = 3.634 ∙ L²

Zone heptagone irrégulière

La zone heptagon irrégulière peut être calculée par triangulation, qui consiste à diviser l'heptagon en cinq triangles (voir la figure suivante). La zone de chacun est calculée et les résultats sont ajoutés, obtenant ainsi la zone complète de l'heptagone.

L'autre méthode est appelée Gaussier déterminant, Et il est nécessaire de placer l'heptagone dans un système de coordonnées rectangulaires, afin de connaître les coordonnées de chaque sommet. La zone est calculée par une formule qui implique les valeurs de ces coordonnées.

Diagonales

Le diagonales Ce sont des segments qui relient un sommet à un autre qui n'est pas consécutif (si le segment relie deux sommets consécutifs côté). Un heptagone a 14 diagonales au total.

Le nombre de diagonales d d'un polygone n'importe quel est calculé à travers la formule:

D = n · (n - 3) / 2

Remplacement n = 7, reste:

D = 7 · (7 - 3) / 2 = 7 · (4/2) = 14

Somme des angles internes

Pour tout heptagone, qu'il soit régulier ou non, la somme de ses angles internes est égal à 900 ° ou 5π radians.

Il peut vous servir: Raisons trigonométriques: exemples, exercices et applications

Cette propriété est très facile à démontrer, car l'heptagone est divisé en triangles individuels qui ne se chevauchent pas, dessinant des segments rectilignes qui unissent les sommets, sans se croiser.

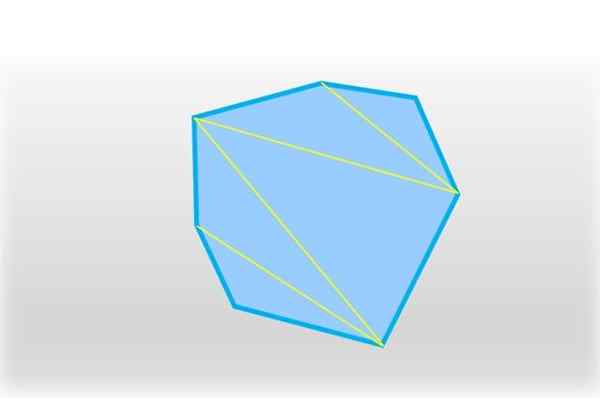Un heptagon peut être divisé en cinq triangles, se joignant à un segment deux sommets non consécutifs. Source: F. Zapata.

Cinq triangles sont obtenus et dans chacun, la somme de ses angles internes est de 180 °, qui multiplié par 5 est égal à 900 °:

5 x 180 ° = 900 °

Formules

Périmètre

Pour un heptagon ordinaire de L, le périmètre P est calculé comme suit:

P = 7⋅l

Si le périmètre est irrégulier, les longueurs de chacun des sept côtés sont ajoutées.

Mesure d'angle interne

Dans un heptagon ordinaire, l'angle interne θ mesure:

θ = [180 (n-2)] / n

Où n = 7.

Apothème

Être le côté de l'heptagone ordinaire. L'apothème est le segment qui va du centre de l'heptagone, perpendiculairement au côté opposé.

Laisser un_p La longueur de l'apothéme. Connaissant le rayon de la circonférence circonscrite, qui est indiquée R_c Et le côté L de l'heptagone, vous avez:

Connaissant l'angle interne θ, ce qui précède est équivalent à:

Zone

S'il s'agit d'un heptagone ordinaire de L, la zone A est donnée par:

A = 3.634 ∙ L²

Lorsque l'heptagone est irrégulier, les coordonnées rectangulaires de chaque sommet sont nécessaires, données par (x_n , et_n), Où n = 1, 2, 3 ... 7.

Ensuite, la formule suivante est appliquée pour trouver la zone A:

Diagonales

Le nombre D des diagonales est donné par:

D = n · (n - 3) / 2

Où n = 7 pour l'heptagone.

Comment faire un heptagone

L'animation suivante montre comment dessiner environ un heptagon ordinaire, en utilisant la règle et la boussole.

Construction de l'heptagone ordinaire. Source: Wikimedia Commons

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Lemonis, m. Calculatrice de Hepalle ordinaire. Récupéré de: Calcrece.com.
3. Référence ouverte en mathématiques. Zone de polygone. Récupéré de: MathpenRef.com.
4. Formules d'univers. Heptagone. Récupéré de: universoformules.com.
5. Wikipédia. Heptagone. Récupéré de: est.Wikipédia.com.