Gravicentro

Quelle est la taxe?

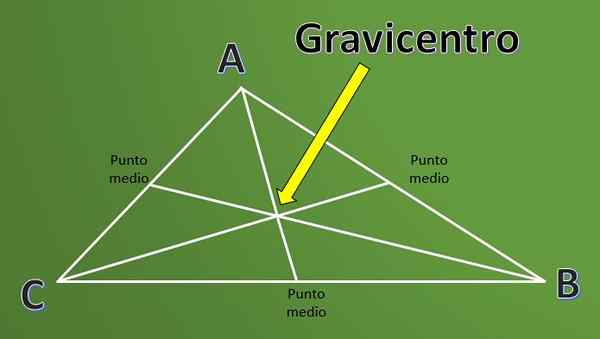
Il Gravicentro C'est une définition qui est largement utilisée en géométrie lorsque vous travaillez avec des triangles. Pour comprendre la définition de Gravicentro, il est d'abord nécessaire de connaître la définition du «milieu» d'un triangle.

Les médianes d'un triangle sont les segments de ligne qui commencent à chaque sommet et atteignent le point médian du côté opposé audit sommet.

Le point d'intersection des trois médianes d'un triangle s'appelle Baricentro ou est également connu sous le nom. Il ne suffit pas de connaître la définition, il est intéressant de savoir comment ce point est calculé.

Calcul du barcentrique

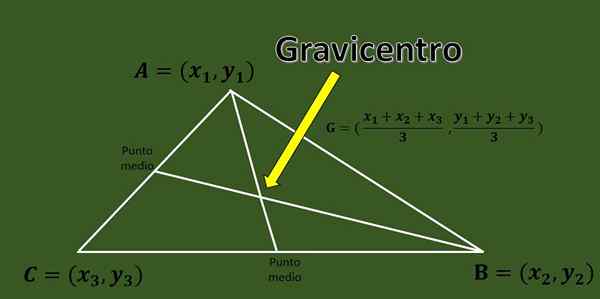
Étant donné un triangle ABC avec des sommets a = (x1, y1), b = (x2, y2) et c = (x3, y3), le Gravicentro est l'intersection des trois médians du triangle.

Une formule rapide qui permet le calcul de la taxation d'un triangle, les coordonnées de ses sommets sont connues:

G = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3).

Avec cette formule, vous pouvez connaître l'emplacement du Gravicentro dans le plan cartésien.

Caractéristiques de la taxe

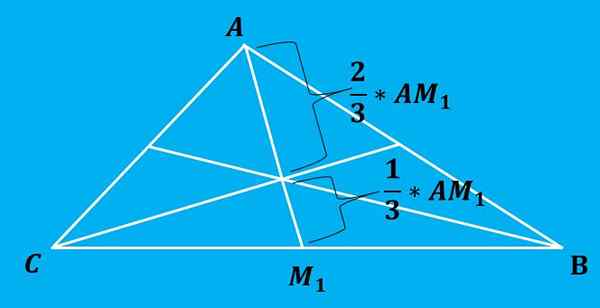
Il n'est pas nécessaire de retracer les trois médianes du triangle, car lorsqu'il en dessinait deux, il sera mis en évidence où la fiscalité est.

Le taxant divise chaque médiane en 2 parties dont la proportion est 2: 1, c'est-à-dire que les deux segments de chaque médiane sont divisés en segments de longueurs 2/3 et 1/3 de la longueur totale, la plus grande distance étant celle là ce qu'il y a entre le sommet et la brochure.

L'image suivante illustre mieux cette propriété.

La formule du calcul de la taxation est très simple à appliquer. La façon d'obtenir cette formule est de calculer les équations droites que chaque médiane définit puis de trouver le point de coupe de ces lignes.

Exercices

Vous trouverez ci-dessous une petite liste de problèmes sur le calcul du baracteur.

1.- Étant donné un triangle de sommets A = (0,0), b = (1,0) et c = (1,1), calculez la fiscalité dudit triangle.

En utilisant la formule donnée, on peut rapidement conclure que le gravicentro du triangle ABC est:

G = ((0 + 1 + 1) / 3, (0 + 0 + 1) / 3) = (2/3, 1/3).

2.- Si un triangle a des sommets A = (0,0), b = (1,0) et c = (1 / 2,1), quelles sont les coordonnées de la taxation?

Étant donné que les sommets du triangle sont connus, la formule du calcul de la fiscalité est appliquée. Par conséquent, Gravicentro a des coordonnées:

G = ((0 + 1 + 1/2) / 3, (0 + 0 + 1) / 3) = (1/2, 1/3).

3.- Calculez les contribuables possibles pour un triangle équilatéral tel que deux de ses sommets sont a = (0,0) et b = (2,0).

Dans cet exercice, seuls deux sommets du triangle sont spécifiés. Afin de trouver les gravcentes possibles, le troisième sommet du triangle doit d'abord calculer.

Étant donné que le triangle est équilatéral et que la distance entre A et B est 2, le troisième sommet C doit être à une distance 2 de A et B.

En utilisant le fait que dans un triangle équilatéral, la hauteur coïncide avec la médiane et en utilisant également le théorème de Pythagore, on peut conclure que les options pour les coordonnées du troisième sommet sont C1 = (1, √3) ou C2 = (1, - - - √3).

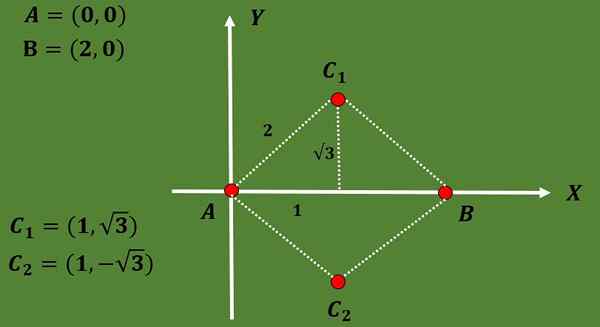
De sorte que les coordonnées des deux gravcentes possibles sont:

G1 = ((0 + 2 + 1) / 3, (0 + 0 + √3) / 3) = (3/3, √3 / 3) = (1, √3 / 3),

G2 = ((0 + 2 + 1) / 3, (0 + 0 --√3) / 3) = (3/3, -√3 / 3) = (1, -√3 / 3).

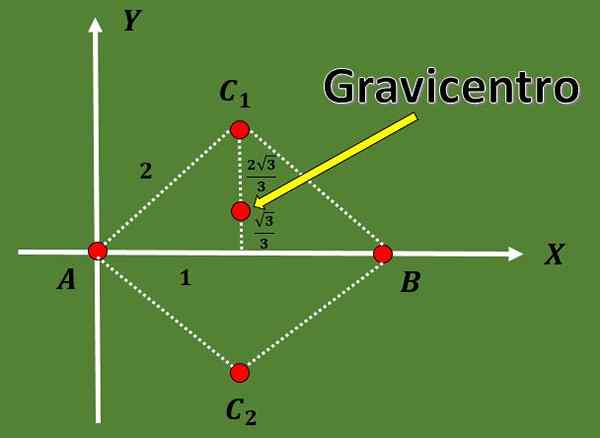
Grâce aux comptes précédents, on peut également noter que la médiane est divisée en deux parties dont la proportion est 2: 1.