Géométrie analytique

Nous expliquons quelle géométrie analytique, son histoire, quelles études et applications

Qu'est-ce que la géométrie analytique?

La géométrie analytique C'est la branche des mathématiques dans laquelle la géométrie et l'algèbre sont combinées, pour résoudre divers problèmes géométriques grâce à des techniques algébriques.

Utiliser des systèmes de coordonnées, tels que le système de coordonnées cartésiennes, qui doit son nom René Descartes. De cette façon, il est possible d'associer les courbes dans le plan et dans l'espace, avec des équations algébriques.

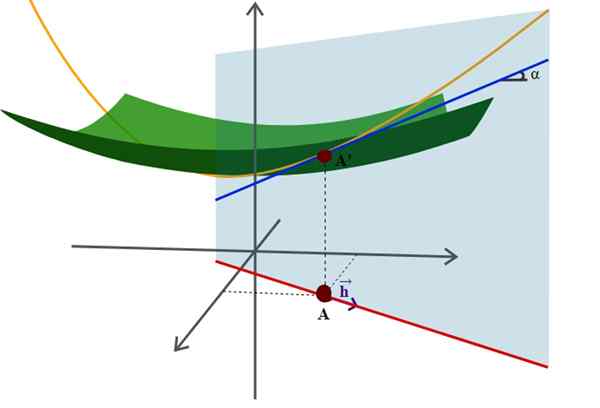
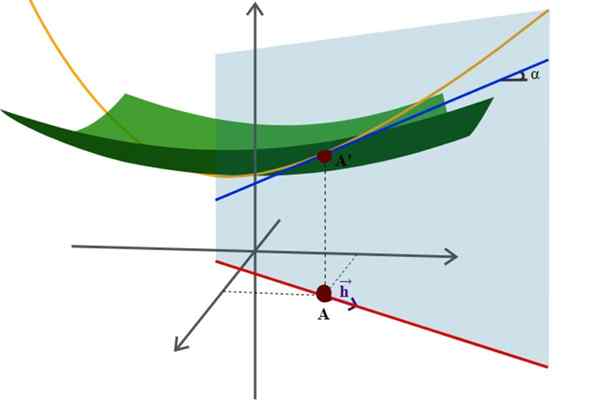Diagramme d'une surface dans l'espace et de son dérivé directionnel, l'une des nombreuses applications plus avancées de la géométrie analytique. Source: Wikimedia Commons.

Un exemple de ceci est l'équation bien connue du rayon r -riortion centré sur l'origine du système de coordonnées:

Sans aucun doute, dans de nombreux cas, il est plus simple de travailler avec l'expression algébrique d'une courbe, qu'avec sa représentation géométrique elle-même. C'est le cas lors du calcul des intersections entre les courbes ou de la recherche de lignes tangentes ou de séchage.

De même, grâce à la géométrie analytique, il est possible de disposer des graphiques de fonctions. Et comme on le sait, les fonctions permettent la modélisation des problèmes de science et d'ingénierie. Par conséquent, la géométrie analytique est présente dans les programmes des carrières associées à ces domaines de connaissance.

Bref historique de la géométrie analytique

La géométrie analytique a son origine dans la première moitié du XVIIe siècle, par la main de deux mathématiciens français notables: René Descartes (1596-1650) et Pierre de Fermat (1601-1665).

René Descartes

Cependant, on peut dire que son arrière-plan remonte à des siècles, au mathématicien grec Apollonius de Pergame (262-190 A.C.). Il a écrit un traité sur les coniques, à laquelle il a accordé leurs noms: circonférence, ellipse, parabole et hyperbole.

Il peut vous servir: proportionnalité composée: explication, trois règles composées, exercices

Ainsi, le travail d'Apollonio a été la base pour, bien plus tard, les Français René Descartes et Pierre de Fermat reposent les fondements de la géométrie analytique, indépendamment. Mais Descartes est considéré comme le père de cette science, car il a été le premier à publier ses œuvres.

Descartes, Fermat et Euler

Dans le discours de la méthode de 1637, Descartes a unifié deux disciplines qui jusque-là avaient été séparées: l'algèbre et la géométrie. Dans son travail, Descartes présente le système de coordonnées cartésiennes, pour localiser des points dans l'avion et dans l'espace.

Il utilise également des équations algébriques de deuxième degré avec deux variables, pour décrire les sections coniques et se consacre à la résolution de problèmes géométriques avec eux. Également pour créer une bonne partie de la notation mathématique qui est actuellement utilisée.

Pierre de Fermat est plus associé à l'optique qu'à la géométrie analytique, cependant, leurs contributions sont notables.

En 1629, Fermat a repris les coniques d'Apollonius de Pergame et a créé les techniques qui composent la géométrie analytique, inventant son propre système de coordonnées et définissant clairement le concept clé de Lieu géométrique, avec lequel commence l'étude de la géométrie analytique.

Cependant, les œuvres de Fermat n'ont vu la lumière qu'en 1679, publiée par son fils, lorsque le mathématicien était déjà mort. Pour cette raison, la paternité de la géométrie analytique est attribuée à Descartes.

Par la suite, aux mathématiciens français, le Suisse Leonardo Euler (1707-1783) a établi les bases formelles de la géométrie analytique. Euler a introduit plusieurs systèmes de coordonnées dans le plan et l'espace: coordonnées rectangulaires, polaires et obliques, ainsi que les transformations d'un système à l'autre.

Peut vous servir: comment les informations sont-elles obtenues dans une enquête?

Dans ses œuvres sur la géométrie analytique, Euler a également approfondi la classification de diverses courbes, selon le degré de l'équation algébrique représentative (troisième et quatrième ordre) et a étudié de manière intensive ses propriétés, les équations des tangentes, des courbures, des symétries et beaucoup plus.

Ce qui étudie la géométrie analytique?

D'une manière générale, la géométrie analytique se concentre sur l'étude des éléments géométriques, tels que des points, des segments, des lignes, des courbes, des surfaces et des volumes. Pour ce faire, comme indiqué ci-dessus, il établit des équations algébriques qui décrivent et relient ces éléments, permettant à leur gestion par le biais de techniques algébriques.

Les principaux objectifs de la géométrie analytique, de manière très sommaire, sont les suivants:

1. Établir le système de coordonnées cartésiennes et le système de coordonnées polaires, pour localiser les points dans l'avion, ainsi que son extension des points dans l'espace.
2. Dessinez des segments, droits, courbes et surfaces sur le plan cartésien et l'espace.
3. Déduire les équations qui décrivent analytiquement une courbe et sa construction sur l'avion et / ou l'espace, ainsi que l'étude de toutes ses propriétés.
4. Classifier les courbes, les surfaces et les volumes.
5. Dériver des formules fondamentales pour résoudre des problèmes sur des points notables, des plans, des plans, des angles, du parallélisme, de la perpendicularité, des distances, des intersections, des zones et plus.
6. Resolver problemas geométricos mediante la aplicación de métodos algebraicos, para lo cual se deducen fórmulas referentes a puntos notables, ecuaciones para la recta, los planos, los ángulos, distancia entre puntos, entre rectas y puntos, puntos de tangencia, rectas secantes, áreas y beaucoup plus.
7. Travailler avec des espaces vectoriels et des produits entre les vecteurs.

Distance entre deux points

À titre d'exemple des nombreuses applications de la géométrie analytique, l'une des plus simples est le calcul de la distance entre deux points du plan. Sont deux points p₁ Et P₂, de coordonnées (x₁,et₁) et (x₂,et₂) respectivement, la distance d entre eux est calculée par:

Peut vous servir: trinomial

Coordonnées polaires

Un point plan peut être spécifié par sa distance «r» à l'origine du système de coordonnées, appelé polo, et l'angle qui forme la ligne qui contient au point et au poteau, avec l'axe horizontal ou l'axe polaire.

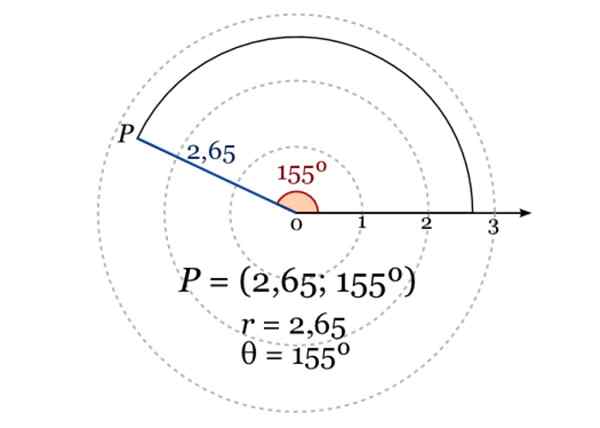L'image montre les coordonnées polaires d'un point P, où r = 2.65 et l'angle en degrés par rapport à l'axe polaire est de 155º. Source: Wikimedia Commons.

Applications de géométrie analytique

Fondation du calcul infinitésimal

La géométrie analytique est essentielle pour le développement du calcul infinitésimal, car il facilite la représentation graphique des courbes et des fonctions, et travaillez avec eux de manière analytique pour créer des modèles qui représentent des phénomènes de nature.

Plans

Le système de coordonnées cartésiennes aide à fabriquer des cartes et à identifier les lieux par la latitude et la longueur, équivalent aux coordonnées cartésiennes d'un point dans le plan.

Calculs topographiques

Différents types de systèmes de coordonnées sont utilisés dans la topographie et constituent la base de leur étude et de leurs applications. Parmi eux, le système de coordonnées polaires décrit ci-dessus.

Trajectoires des corps célestes

Les sections coniques, décrites par géométrie analytique, participent à des phénomènes importants de la nature, tels que les trajectoires des corps célestes, soumis à la force de la gravité. Par exemple, les planètes et certaines comètes décrivent des trajectoires elliptiques autour du soleil, avec celle située dans l'un des projecteurs.

Architecture civile et construction

De nombreuses courbes font partie des constructions architecturales, par exemple, les câbles d'un pont suspendu peuvent prendre la forme de paraboles.

Systèmes de positionnement mondial

Le système de positionnement global ou le GPS rend les emplacements possibles avec précision, ainsi que des objets en mouvement, tels que les véhicules et les bateaux. Cela aide également les gens à atteindre plus facilement leurs destinations, en les guidant sur les meilleures itinéraires.