Types de fonctions transcendantes, définition, propriétés, exemples

Le fonctions transcendantes Les élémentaires sont des fonctions trigonométriques exponentielles, logarithmiques, trigonométriques, inverses, hyperboliques et hyperboliques inverses. C'est-à-dire que ce sont ceux qui ne peuvent pas être exprimés par un rapport polynomial, polynomial ou polynomial. 

Les fonctions transcendantes non élémentaires sont également connues sous le nom de fonctions spéciales et parmi lesquelles la fonction d'erreur peut être nommée. Le fonctions algébriques (polynômes, quotients polynomiaux et racines polynomiales) à côté du fonctions transcendantes Les élémentaires constituent ce qui est connu en mathématiques fonctions élémentaires.

Il est également considéré comme des fonctions transcendantes résultant des opérations entre les fonctions transcendantes ou entre les fonctions transcendantes et algébriques. Ces opérations sont: la somme et la différence des fonctions, le produit et le rapport des fonctions, ainsi que la composition de deux ou plusieurs fonctions.

[TOC]

Définition et propriétés

Fonction exponentielle

C'est une véritable fonction de la variable indépendante réelle de la forme:

f (x) = a ^ x = a^X

où pour C'est un nombre réel positif (A> 0) fixe appelé la base. Circumflejo ou la supervision sont utilisés pour indiquer l'opération de potentialisation.

Mettons-nous au cas A = 2 Ensuite, la fonction est comme ceci:

f (x) = 2 ^ x = 2^X

Qui sera évalué pour plusieurs valeurs de la variable indépendante x:

Vous trouverez ci-dessous un graphique où la fonction exponentielle pour plusieurs valeurs de base est représentée, y compris la base et (Numéro de neper et ≃ 2.72). Base et Il est si important que, en général, lorsque vous parlez de fonction exponentielle, vous pensez à E ^ x, qui est également indiqué Exp (x).

Figure 1. Fonction exponentielle a ^ x, pour plusieurs valeurs de la base a. (Élaboration propre)

Propriétés de la fonction exponentielle

À partir de la figure 1, on peut voir que le domaine des fonctions exponentiels est des nombres réels (Dom f = R) et la gamme ou l'itinéraire sont les vrais positifs (Ran f = R⁺). 

Peut vous servir: symétrie

D'un autre côté, quelle que soit la valeur de la base A, toutes les fonctions exponentielles passent par le point (0, 1) et par point (1, a). 

Quand la base A> 1, Alors la fonction augmente et quand 0 < a < 1 La fonction diminue. 

Les courbes de y = a ^ x et de y = (1 / a) ^ x  Ils sont symétriques par rapport à l'axe ET. 

À l'exception de l'affaire A = 1, La fonction exponentielle est injective, c'est-à-dire à chaque valeur de l'image, on correspond et seulement une valeur de départ.

Fonction logarithmique

C'est une fonction réelle réelle d'une variable indépendante réelle basée sur la définition du logarithme d'un nombre. Basé sur le logarithme pour d'un nombre X, C'est le numéro et à laquelle la base doit être soulevée pour obtenir l'argument X:

enregistrer_pour(x) = y ⇔ a ^ y = x

C'est le fonction de logarithme fondé pour C'est la fonction inverse de la fonction exponentielle basée sur pour.

Par exemple:

enregistrer₂1 = 0, depuis 2 ^ 0 = 1

Un autre cas, journal₂4 = 2, car 2 ^ 2 = 4

Le logarithme racine de 2 est le journal₂√2 = ½, car 2 ^ ½ = √2

enregistrer₂ ¼ = -2, en vue que 2 ^ (-2) = ¼ 

Vous trouverez ci-dessous un graphique de la fonction de logarithme dans diverses bases.

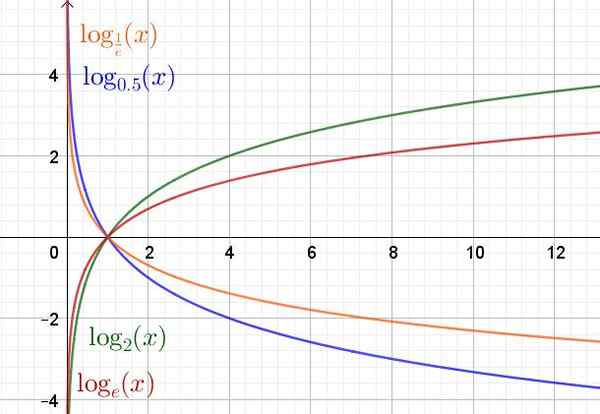Figure 2. Fonction exponentielle pour différentes valeurs de base. (Élaboration propre)

Propriétés de la fonction logaritmo

Le domaine de la fonction de logarithme et (x) = logarithmepour(X)  Ce sont les nombres réels positifs R+. La plage ou l'itinéraire sont les nombres réels R.

Quelle que soit la base, la fonction de logarithme passe toujours par le point (1.0) et le point (a, 1) appartient au graphique de ladite fonction.

Il peut vous servir: Théorie de la file d'attente: histoire, modèle, à quoi sert-il pour et des exemples pour

Dans le cas où la base A est supérieure à l'unité (a> 1), la fonction de logarithme augmente. Mais oui (0 < a < 1) entonces es una función decreciente.

Seno, Coseno et fonctions tangentes

La fonction sinusoïdale attribue un nombre réel et à chaque valeur x, où x représente la mesure d'un angle dans les rayons. Pour obtenir la valeur de Sen (x) sous un angle, l'angle est représenté dans le cercle unitaire et la projection dudit angle sur l'axe vertical est le sein correspondant à cet angle.

Ci-dessous est (dans la figure 3) le cercle trigonométrique et le sein pour plusieurs valeurs angulaires x1, x2, x3 et x4.

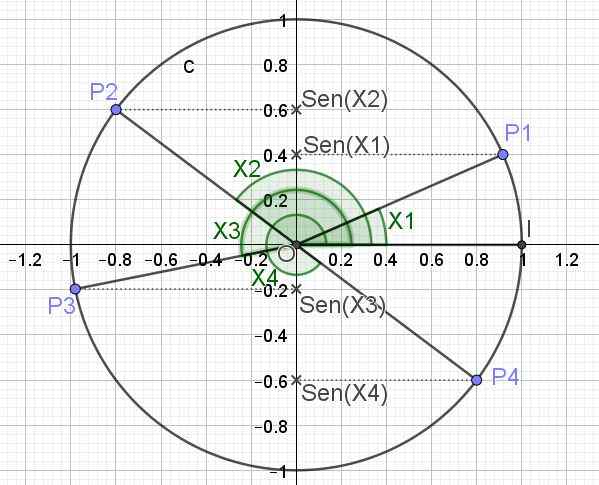figure 3. Cercle trigonométrique et sein de plusieurs angles. (Élaboration propre)

Défini de cette manière la valeur maximale que la fonction SEN (x) peut avoir est 1, qui se produit lorsque x = π / 2 + 2π n, étant n un entier (0, ± 1, ± 2,). La valeur minimale que la fonction Sen (x) peut prendre lorsque x = 3π / 2 + 2π n. 

La fonction coseno y = cos (x) est définie d'une manière similaire, mais la projection des positions angulaires p1, p2, etc. est réalisée sur l'axe horizontal du cercle trigonométrique.

D'un autre côté, la fonction y = tan (x) est le rapport entre la fonction sinus et la fonction cosinus.

Ensuite, un graphique des fonctions transcendants SEN (x), cos (x) et tan (x) est montré

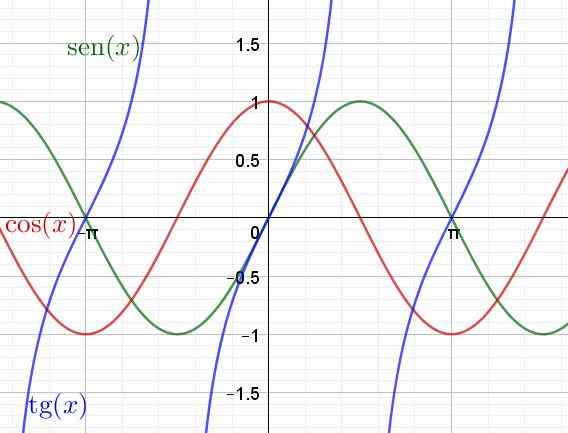Figure 4. Graphique des fonctions transcendantes, sein, cosinus et tangente. (Élaboration propre)

Dérivé et intégral

Dérivé de la fonction exponentielle

Le dérivé et' de la fonction exponentielle y = a ^ x C'est la fonction a ^ x multiplié par lui Logarithme népérienne de la base a:

Peut vous servir: Théorie des ensembles: caractéristiques, éléments, exemples, exercices

et '= (a ^ x)' = a ^ x ln a

Dans le cas particulier de la base et, La dérivée de la fonction exponentielle est la fonction exponentielle elle-même.

Intégrale de la fonction exponentielle

L'intégrale indéfinie de a ^ x C'est la fonction divisée entre le logarithme népérienne de la base. 

Dans le cas particulier de la base E, l'intégrale de la fonction exponentielle est la fonction exponentielle elle-même.

Tableau dérivé et intégral des fonctions transcendantes

Vous trouverez ci-dessous un tableau récapitulatif des principales fonctions transcendantes, ses dérivés et indéfinis (antidérivatifs):

Tableau dérivé et intégrale indéfini pour certaines fonctions transcendantes. (Élaboration propre)

Exemples

Exemple 1

Trouvez la fonction résultante de la composition de la fonction f (x) = x ^ 3 avec la fonction g (x) = cos (x):

(f ou g) (x) = f (g (x)) = cos³(X)

Son dérivé et son intégrale indéfini sont:

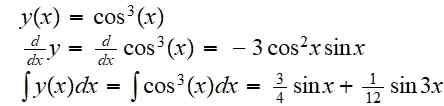
Exemple 2

Trouvez la composition de la fonction G avec la fonction F, étant g et f les fonctions définies dans l'exemple précédent:

(g ou f) (x) = g (f (x)) = cos (x³)

Il convient de noter que la composition des fonctions n'est pas une opération commutative.

La dérivée et l'intégrale indéfinie de cette fonction sont respectivement:

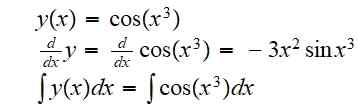
L'intégrale a été laissée indiquée car il n'est pas possible d'écrire le résultat en tant que combinaison de fonctions élémentaires de manière exacte.

Les références

1. Calcul d'une seule variable. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 novembre. 2008
2. Le théorème de la fonction implicite: histoire, théorie et applications. Steven G. Krantz, Harold R. Parcs. Springer Science & Business Media, 9 novembre. 2012
3. Analyse multivariée. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 décembre. 2010
4. Dynamique du système: modélisation, simulation et contrôle des systèmes mécatroniques. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 mars. 2012
5. Calcul: mathématiques et modélisation. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1er janvier. 1999
6. Wikipédia. Fonction transcendante. Récupéré de: est.Wikipédia.com