Coefficient de frottement visqueux (force) et exemples

La frottement visqueux Il survient lorsqu'un objet solide se déplace au milieu d'un gaz fluide ou d'un liquide-. Il peut être modélisé comme une force proportionnelle au négatif de la vitesse de l'objet ou du carré.

L'utilisation d'un ou l'autre modèle dépend de certaines conditions, comme le type de liquide dans lequel l'objet est déplacé et s'il est très rapide ou non. Le premier modèle est connu sous le nom Résistance linéaire, et en elle l'ampleur de la friction visqueuse F_touche Il est donné par:

F_touche = Γv

Figure 1. Les paracharidistes éprouvent une force visqueuse pendant leur descente, car l'air offre une résistance. Source: Pixabay.

Ici γ est la constante de proportionnalité ou de coefficient de frottement visqueux et V est la rapidité de l'objet. Il est applicable aux corps qui se déplacent à des vitesses à faible fluide avec le régime laminaire.

Dans le deuxième modèle, connu sous le nom Résistance quadratique o Rayleight's Law, l'ampleur de la force de friction est calculée selon:

F_touche = ½ ρ.POUR.C_d.V²

Où ρ est la densité du fluide, a est la zone de section croisée de l'objet et c_d C'est le coefficient de résistance aérodynamique.

Le produit ½ ρ.POUR.C_d  Il s'agit d'une aérodynamique constante appelée D, dont les unités sont donc kg / m:

F_touche = DV²

Ce modèle est plus approprié lorsque la vitesse des objets est moyenne ou élevée, car le mouvement produit des turbulences ou des tourbillons sur son chemin dans le fluide.

Une balle de tennis en mouvement et les voitures sur l'autoroute sont des exemples d'objets dans lesquels ce modèle fonctionne assez bien.

La force de viscose survient parce que le solide doit prendre les couches de fluide pour pouvoir le traverser. L'existence de plusieurs modèles est que cette force dépend de plusieurs facteurs, tels que la viscosité du fluide, la vitesse et la forme de l'objet.

Peut vous servir: qu'est-ce que la perméabilité relative?

Il y a plus d'objets aérodynamiques que d'autres et beaucoup sont conçus précisément afin que la résistance du milieu réduit sa vitesse à un minimum.

[TOC]

Exemples de frottement de viscose

Toute personne ou objet qui se déplace dans un liquide éprouve nécessairement une résistance de l'environnement, mais plusieurs fois ces effets sont méprisés pour des applications simples telles que la chute libre.

Dans les déclarations de presque tous les problèmes de chute libre, il est à noter que les effets de la résistance à l'air se méprisent. En effet.

Mais il y a d'autres mouvements dans lesquels la friction visqueuse a une influence plus décisive, voyons quelques exemples:

Des pierres qui tombent dans l'eau et les grains de pollen

-Un rocher qui tombe verticalement dans un tube plein d'huile éprouve une force qui s'oppose à sa descente, grâce à la résistance aux fluides.

-Les grains de pollen sont très petits, donc pour eux, la résistance de l'air n'est pas négligeable, car grâce à cette force, ils parviennent à rester à flot pendant longtemps, provoquant des allergies saisonnières.

Figure 2. Les grains de pollen sont suffisamment petits pour que la résistance à l'air ait un effet significatif. Source: pikrepo.

Nageurs et cyclistes

-Dans le cas des nageurs, ils utilisent un chapeau et ils se rasent complètement pour que la résistance de l'eau ne soustraire pas la vitesse.

-Comme les nageurs, les cyclistes de contre-litre éprouvent une résistance à l'air, par conséquent les casques ont des conceptions aérodynamiques pour améliorer l'efficacité.

La position du cycliste au sein d'un groupe en compétition est pertinente. Celui qui dirige la marche reçoit évidemment la plus grande résistance de l'air, tandis que pour ceux qui ferment la marche, c'est presque nulle.

Il peut vous servir: deuxième condition d'équilibre: explication, exemples, exercices

Paracharides

-Une fois qu'un paratrooper ouvre le parachute, il est exposé à la friction visqueuse de l'air, étant le modèle le plus approprié qui a le carré de la vitesse. De cette façon, il réduit sa vitesse et comme le frottement est opposé à la chute, il atteint une valeur limite constante.

Voitures

-Pour les voitures, le coefficient de résistance aérodynamique, une constante qui est déterminée expérimentalement et la surface qu'elle présente contre le vent, sont les facteurs déterminants pour réduire la résistance à l'air et réduire la consommation. C'est pourquoi ils sont conçus avec des pare-brise inclinés.

Expérience de chute d'huile de Millikan

-Dans l'expérience de chute de pétrole Millikan, le physicien Robert Millikan a étudié le mouvement des gouttes d'huile au milieu d'un champ électrique uniforme, concluant que toute charge électrique est multiple de la charge électronique.

Pour cela, il était nécessaire de connaître le rayon des gouttes, qui ne pouvait pas être déterminée par mesure directe, étant donné sa petite taille. Mais dans ce cas, la friction visqueuse était importante et les gouttes ont fini par freiner. Ce fait a permis de déterminer le rayon des gouttes puis sa charge électrique.

Exercices

- Exercice 1

Dans l'équation de la force de frottement visqueuse à basse vitesse:

F_touche = Γv

a) Quelles dimensions le coefficient de frottement visqueux devrait-il avoir γ?

b) Quelles sont les unités γ dans le système international d'unités?

Solution à

Contrairement aux coefficients de frottement statiques ou cinétiques, le coefficient de frottement visqueux a des dimensions, qui doivent être:

Peut vous servir: Adhésion physique: qu'est-ce que et des exemples

Force / vitesse

La force a des dimensions de masse x longueur / temps², tandis que les vitesses sont de longueur / temps. En les indiquant comme suit:

-Messe: m

-Longueur: L

-Temps: t

Les dimensions du coefficient de frottement visqueux γ sont:

[M.L / T²] / [L / t] = [m.L.T / l.T²] = M / t

Solution B

Dans le Si, les unités γ sont kg / s

- Exercice 2

Compte tenu de la résistance que l'eau s'oppose, trouvant une expression pour la vitesse terminale d'une sphérite métallique qui tombe verticalement dans un tube plein d'huile, dans les cas:

a) Basse vitesse

b) Haute vitesse

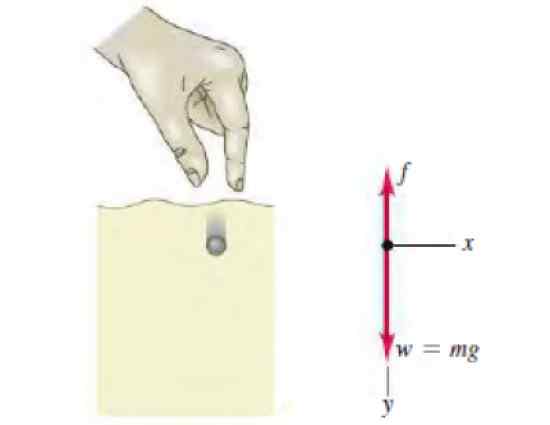figure 3. Diagramme corporel libre d'une sphérite qui descend à l'intérieur d'un fluide. Source: Sears, Z. Physique universitaire avec physique moderne.

Solution à

Dans la figure, le diagramme du corps libre apparaît, montrant les deux forces qui agissent sur la sphérite: le poids en baisse et la résistance du fluide, proportionnelle à la vitesse, vers le haut. La deuxième loi de Newton pour ce mouvement établit ce qui suit:

γv_t - mg = 0

Où V_t C'est la vitesse terminale, donnée par:

V_t = mg / γ

Solution B

Si nous supposons que la moyenne à des vitesses élevées, le modèle approprié est celui avec une vitesse carrée:

F_touche = ½ ρ.POUR.C_d.V²

Ensuite:

½ ρ.POUR.C_d.V² - mg = 0

D.V² - mg = 0

v = √ [mg / d]

Dans les deux situations, plus la masse de l'objet est grande, plus sa vitesse terminale est grande.

Les références

1. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Élégant. Cengage Learning.
2. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1.
3. Tipler, P. (2006) Physique de science et de technologie. 5e ed. Volume 1. Éditorial Revered.
4. Tippens, P. 2011. Physique: concepts et applications. 7e édition. McGraw Hill
5. Université de Séville. Frottements. Récupéré de: Laplace.nous.est.