Facteur de compressibilité comment calculer, exemples et exercices

Il Facteur de compressibilité z, o Le facteur de compression pour les gaz, est une valeur sans dimension (sans unités) qui est introduite comme une correction dans l'équation de statut de gaz idéal. De cette façon, le modèle mathématique ressemble plus au comportement observé du gaz.

Dans le gaz idéal, l'équation d'état qui se rapporte aux variables p (pression), V (volume) et t (température) est: P.V _idéal = n.R.T avec n = nombre de moles et r = constante des gaz idéaux. Ajout de la correction du facteur de compression Z, cette équation est transformée en:

P.V = z.n.R.T

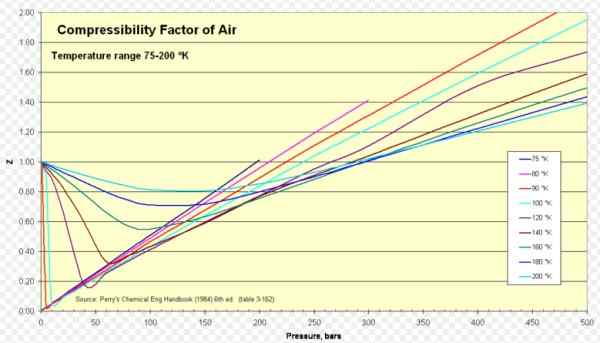
Figure 1. Facteur de compressibilité de l'air. Source: Wikimedia Commons. https: // télécharger.Wikimedia.org / wikipedia / commons / 8/84 / compressibility_factor_of_air_75-200_k.PNG.

[TOC]

Comment calculer le facteur de compressibilité?

Compte tenu de ce volume molaire V_cool = V / n, Vous avez le vrai volume molaire:

P . V_réel = Z. R. T → Z = PV _réel/ Rt

Étant donné que le facteur de compressibilité Z dépend des conditions de gaz, elle est exprimée en fonction de la pression et de la température:

Z = z (p, t)

En comparant les deux premières équations, il est à noter que si le nombre de moles N est égal à 1, le volume molaire d'un gaz réel est lié à celui du gaz idéal à travers:

V_réel / V_idéal = Z → v _réel = Z v_idéal

Lorsque la pression dépasse les 3 atmosphères, la plupart des gaz s'arrêtent comme des gaz idéaux et le volume réel diffère considérablement de l'idéal.

Cela s'est rendu compte dans ses expériences du physicien néerlandais Johannes van der Waals (1837-1923), ce qui l'a amené à créer un modèle qui s'est mieux adapté aux résultats pratiques que l'équation des gaz idéaux: l'équation de l'État de van der Waals.

Peut vous servir: oxalate de sodium (NA2C2O4): Structure, propriétés, utilisations, risques

Exemples

Selon l'équation P.V_réel= Z.n.Rt, Pour un gaz idéal, z = 1. Cependant, dans les gaz réels, en augmentant la pression, fait également la valeur de z. Cela a du sens car à une plus grande pression, les molécules de gaz ont plus de possibilités de collision, donc les forces de répulsion augmentent et ainsi le volume.

D'un autre côté à des pressions plus faibles, les molécules se déplacent avec une plus grande liberté et les forces de répulsion diminuent. Par conséquent, un volume inférieur est attendu. Quant à la température, lorsqu'il augmente, Z diminue.

Comme l'a observé Van der Waals, au voisin.

Le point critique (t_c, P_c) de toute substance sont les valeurs de pression et de température qui déterminent leur comportement avant un changement de phase:

-T_c C'est la température au-dessus duquel le gaz en question n'est pas liquéfié.

-P_c  C'est la pression minimale nécessaire pour liquéfier le gaz à la température t_c

Chaque gaz a cependant son propre point critique, définissant la température et la pression réduite t_r Et P_r comme suit:

P_r = P / p_c

V_r = V / v_c

T_r = T / T_c

Il est observé qu'un gaz confiné avec V_r et T_r exercer la même pression P_r. Pour cette raison, si z est graphique en fonction de P_r à la même T_r, Chaque point de cette courbe est le même pour tout gaz. C'est appelé Principe des États correspondants.

Le facteur de compressibilité dans les gaz idéaux, l'air, l'hydrogène et l'eau

Vous trouverez ci-dessous une courbe de compressibilité pour divers gaz à différentes températures réduites. Puis quelques exemples de z pour certains gaz et une procédure pour trouver z en utilisant la courbe.

Peut vous servir: hydrogène: histoire, structure, propriétés et utilisations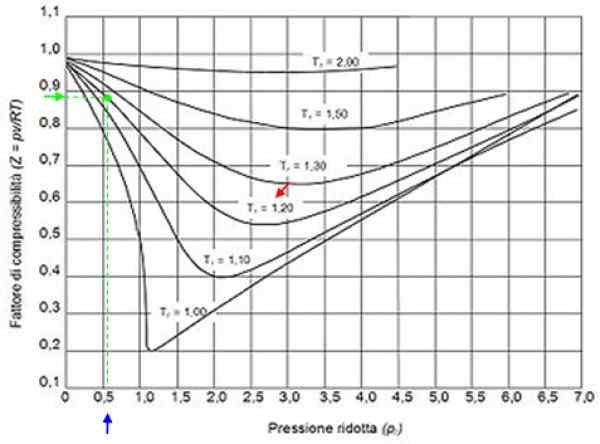Figure 2. Facteur graphique graphiques pour les gaz en fonction de la pression de réduction. Source: Wikimedia Commons.

Gaz idéaux

Les gaz idéaux ont z = 1, comme expliqué au début.

Air

Pour l'air z est d'environ 1 dans une vaste gamme de températures et de pressions (voir figure 1), où le modèle de gaz idéal donne de très bons résultats.

Hydrogène

Z> 1 pour toutes les pressions.

Eau

Pour trouver Z de l'eau, les valeurs du point critique sont nécessaires. Le point critique de l'eau est: P_c = 22.09 MPA et T_c= 374.14 ° C (647.3 k). Encore une fois, il est nécessaire de prendre en compte que le facteur de compressibilité Z dépend de la température et de la pression.

Par exemple, supposons que vous souhaitiez trouver z de l'eau à 500 ºC et 12 MPa. Alors le premier consiste à calculer la température réduite, pour laquelle les degrés Celsius doivent être transmis à Kelvin: 50 ºC = 773 K:

T_r = 773/647.3 = 1.2

P_r = 12/22.09 = 0.54

Avec ces valeurs, nous localisons dans le graphique de la figure, la courbe correspondant à t_r = 1.2, indiqué par une flèche rouge. Ensuite, nous regardons dans l'axe horizontal la valeur de p_r plus proche de 0.54, marqué en bleu. Maintenant, nous dessinons une verticale jusqu'à intercepter la courbe T_r = 1.2 et enfin il est projeté à partir de ce point à l'axe vertical, où nous lisons la valeur approximative de z = 0.89.

Exercices résolus

Exercice 1

Il y a un échantillon de gaz à une température de 350 K et une pression de 12 atmosphères, avec un volume molaire de 12% plus élevé que celui prévu par la loi sur les gaz idéaux. Calculer:

A) Facteur de compression Z.

b) Volume molaire de gaz.

Peut vous servir: réaction irréversible: caractéristiques et exemples

c) Selon les résultats ci-dessus, indiquez quelles sont les forces dominantes de cet échantillon de gaz.

Données: r = 0,082 L.atm / mol.K

Solution à

Sachant que V _réel  est 12% plus élevé que V_idéal :

V_réel  = 1.12V_idéal

Z = V _réel / V_idéal = 1.12

Solution B

P . V_réel = Z. R. T → V_réel = (1.12 x 0.082 x 350/12) l / mol = 2.14 L / mol.

Solution C

Les forces de répulsion sont celles qui prédominent, puisque le volume de l'échantillon a augmenté.

Exercice 2

Il y a 10 moles d'éthane confinés dans un volume de 4.86 L A 27 ºC. Trouvez la pression exercée par l'éthane de:

a) Le modèle de gaz idéal

b) l'équation de van der Waals

c) Trouvez le facteur de compression des résultats précédents.

Données pour l'éthane

Coefficients de van der Waals:

A = 5.489 DM⁶. AU M . mol^-2  et b = 0.06380 DM³. mol^-1.

Pression critique: 49 ATM. Température critique: 305 K

Solution à

La température est transmise à Kelvin: 27 º C = 27 +273 K = 300 K, n'oubliez pas que 1 litre = 1 l = 1 dm³.

Ensuite, les données fournies dans l'équation de gaz idéale sont remplacées:

P.V = n.R.T → P = (10 x 0,082 x 300/4.86 l) atm = 50.6 atm

Solution B

L'équation de l'État de Van der Waals est:

Où a et b sont les coefficients donnés par la déclaration. Lors de la défrichement p:

Solution C

Nous calculons la pression et la température réduites:

P_r = 35.2/49 = 0.72

T_r = 300/305 = 0.98 ≈ 1

Avec ces valeurs, la valeur de Z dans le graphique de la figure 2 est recherchée, constatant que z est environ 0.7.

 Les références

1. Atkins, P. 1999. Chimie physique. Éditions Omega.
2. Cengel, et. 2012. Thermodynamique. 7^mame Édition. McGraw Hill.
3. Engel, T. 2007. Introduction à la physicochimie: thermodynamique. Pearson.
4. Levine, je. 2014. Principes de la chimie physique. 6e. Édition. McGraw Hill.
5. Wikipédia. Facteur de compressibilité. Récupéré de: dans.Wikipédia.org.