Espace vecteur de base et de dimension, axiomes, propriétés

UN espace vectoriel C'est un ensemble non empty V= ou, V, W,…, dont les éléments sont des vecteurs. Avec eux, certaines opérations importantes sont effectuées, parmi lesquelles les éléments suivants se démarquent:

- Somme entre deux vecteurs U + V par conséquent z, qui appartient à l'ensemble V.

- Multiplication d'un nombre réel α par un vecteur V: α V qui donne un autre vecteur et qui appartient à V.

Vision artistique d'un espace vectoriel. Source: Pixabay

Pour désigner un vecteur, nous utilisons audacieux (V C'est un vecteur), et pour les scalaires ou les nombres des lettres grecques (α est un nombre).

[TOC]

Axiomes et propriétés

Pour être un espace vectoriel, les huit axiomes suivants doivent être remplis:

1-conmubabilité: ou +V = V +ou

2-transitivité: (ou + V) + W = ou + ( V + W)

3-existence du vecteur nul 0 tel que 0 + V = V

4-existence de l'opposé: l'opposé de V est (-V) , car V + (-V) = 0

Distributivité 5-Product par rapport à la somme vectorielle: α ( ou + V ) = αou +αV

Distributivité 6-Product par rapport à la somme scalaire: (α + β)V = αV +βV

7-associativité du produit scalaire: α (β V) = (α β)V

8-le numéro 1 C'est l'élément neutre depuis: 1V = V

Exemples d'espaces vectoriels

Exemple 1

Les vecteurs dans le plan (R²) sont un exemple d'espace vectoriel. Un vecteur dans le plan est un objet géométrique qui a l'ampleur et la direction. Il est représenté par un segment orienté qui appartient audit plan et avec une taille proportionnelle à son ampleur.

La somme de deux vecteurs dans le plan peut être définie comme l'opération géométrique du deuxième vecteur après le premier. Le résultat de la somme est le segment orienté qui commence à l'origine du premier et atteint la pointe du second.

Dans la figure, on peut noter que la somme en R² est commutative.

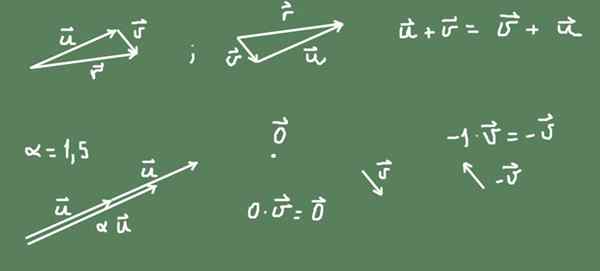Figure 2. Vecteurs dans le plan de l'espace vectoriel. Source: auto-faite.

Le produit d'un nombre α est également défini par un vecteur. Si le nombre est positif, l'adresse du vecteur d'origine est maintenue et la taille est α fois le vecteur d'origine. Si le nombre est négatif, l'adresse est l'inverse et la taille du vecteur résultant est la valeur absolue du nombre.

Le vecteur opposé à un vecteur tout V est -V = (-1) V.

Le vecteur nul est un point dans le plan R², et le nombre zéro par un vecteur entraîne le vecteur nul.

Tout dit est illustré dans la figure 2.

Exemple 2

Ensemble P De tous les polynômes inférieurs ou égaux à deux, y compris la note zéro, ils forment un ensemble qui rencontre tous les axiomes d'un espace vectoriel.

Il peut vous servir: événements mutuellement exclusifs: propriétés et exemples

Être le polynôme p (x) = a x² + b x + c y q (x) = d x² + e x + f

La somme de deux polynômes est définie: p (x) + q (x) = (a + d) x² + (b + e) ​​x + (c + f)

La somme des polynômes appartenant à l'ensemble P C'est commutatif et transitif.

Le polynôme nul appartenant à l'ensemble P C'est celui qui a tous ses coefficients égaux à zéro:

0 (x) = 0 x² + 0 x + 0

La somme d'un scalaire α est définie par un polynôme tel que: α p (x) = α ∙ a x² + α ∙ b x + α ∙ c

Le polynôme opposé de p (x) est -p (x) = (-1) p (x).

De tout ce qui précède, il s'ensuit que l'ensemble P De tous les polynômes inférieurs ou égaux à deux, c'est un espace vectoriel.

Exemple 3

Ensemble M De toutes les matrices de M lignes x n colonnes dont les éléments sont des nombres réels forment un réel espace vectoriel, en ce qui concerne la somme des matrices et le produit d'un nombre par une matrice.

Exemple 4

L'ensemble F des fonctions continues de la variable réelle, forment un espace vectoriel, puisque la somme de deux fonctions peut être définie, la multiplication d'un scalaire par une fonction, la fonction nul et la fonction symétrique. Ils remplissent également les axiomes qui caractérisent un espace vectoriel.

Base et dimension d'un espace vectoriel

Base

Un ensemble de vecteurs linéairement indépendants est défini comme la base d'un espace vectoriel tel que, à partir d'une combinaison linéaire, tout vecteur de cet espace vectoriel peut être généré.

La combinaison linéaire de deux vecteurs ou plus consiste à multiplier les vecteurs par un scalaire puis à les ajouter vectoriel.

Par exemple, dans l'espace vectoriel du vecteur en trois dimensions formées par R³, la base canonique définie par les vecteurs unitaires (de magnitude 1) est utilisée (de magnitude 1) Toi, J, k.

Où Toi = (1, 0, 0); J = (0, 1, 0); k = (0, 0, 1). Ce sont des vecteurs cartésiens ou canoniques.

Tout vecteur V appartenant à r³ est écrit comme V = A Toi + b J + c k, qui est une combinaison linéaire de vecteurs de base Toi, J, k. Les scalaires ou les nombres a, b, c sont connus sous le nom de composants cartésiens de V.

On dit également que les vecteurs de base d'un espace vectoriel forment un ensemble d'espace vectoriel.

Dimension

La dimension d'un espace vectoriel est le nombre cardinal d'une base vectorielle pour ledit espace; c'est-à-dire le nombre de vecteurs qui composent ladite base.

Ce cardinal est le nombre maximum de vecteurs linéairement indépendants de cet espace vectoriel, et en même temps le nombre minimum de vecteurs qui forment un ensemble de génération de cet espace.

Peut vous servir: Population statistique: concept, types, exemples

Les bases d'un espace vectoriel ne sont pas uniques, mais toutes les bases du même espace vectoriel ont la même dimension.

Sous-espace vectoriel

Un sous-espace vectoriel d'un espace vectoriel V est un sous-ensemble de V dans lequel les mêmes opérations sont définies comme dans V et remplit tous les axiomes de l'espace vectoriel. Par conséquent, le sous-espace sera également un espace vectoriel.

Un exemple de sous-espace vectoriel est les vecteurs qui appartiennent au plan XY. Ce sous-espace est un sous-ensemble d'un espace vectoriel de dimensionnalité supérieur à l'ensemble de vecteurs appartenant à l'espace à trois dimensions xyz.

Un autre exemple de sous-espace vectoriel S1 de l'espace vectoriel est formé par toutes les matrices 2 × 2 avec des éléments réels est celui défini ci-dessous:

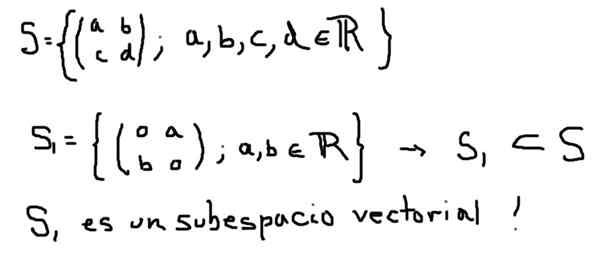
D'un autre côté, S2 a défini ci-dessous, bien qu'il s'agisse d'un sous-ensemble de S, il ne forme pas de sous-espace vectoriel:

Exercices résolus

-Exercice 1

Être les vecteurs V1= (1, 1, 0); V2= (0, 2, 1) et V3= (0, 0, 3) dans r³.

a) prouver qu'ils sont linéairement indépendants.

b) prouver qu'ils forment une base en r³, car toute liste (x, y, z) peut être écrite comme une combinaison linéaire de v1, v2, v3.

c) Trouvez les composants de la liste V = (-3,5,4) à la base V1, V2, V3.

Solution

Le critère pour démontrer l'indépendance linéaire est d'établir l'ensemble suivant d'équations dans α, β et γ

α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)

Dans le cas où la seule solution à ce système est α = β = γ = 0, alors les vecteurs sont linéairement indépendants, sinon ils ne sont pas.

Pour atteindre les valeurs de α, β et γ, nous proposons le système d'équations suivant:

α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0

α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0

α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0

Le premier conduit à α = 0, le deuxième α = -2 ∙ β mais comme α = 0 alors β = 0. La troisième équation implique que γ = (-1/3) β, mais comme β = 0 alors γ = 0.

Réponds à

Il est conclu qu'il s'agit d'un ensemble de vecteurs linéairement indépendants dans R³ .

Réponse b

Écrivons maintenant la liste (x, y, z) comme une combinaison linéaire de v1, v2, v3.

(x, y, z) = α v1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)

α ∙ 1 + β ∙ 0 + γ ∙ 0 = x

α ∙ 1 + β ∙ 2 + γ ∙ 0 = y

Il peut vous servir: Test de Tukey: qu'est-ce que, en cas d'exemple, un exercice résolu

α ∙ 0 + β ∙ 1 + γ ∙ 3 = z

Où vous avez:

α = x

α + 2 β = y

β + 3 γ = z

Le premier indique α = x, le deuxième β = (y-x) / 2 et le troisième γ = (z- y / 2 + x / 2) / 3. De cette façon, nous avons trouvé les générateurs de α, β et γ de toute liste R³ 

Réponse C

Trouver les composants de la liste V = (-3,5,4) à la base V1, V2, V3.

Nous remplaçons les valeurs correspondantes dans les expressions trouvées ci-dessus pour les générateurs.

Dans ce cas, nous avons: α = -3; β = (5 - (- 3)) / 2 = 4; γ = (4- 5/2 + (- 3) / 2) / 3 = 0

C'est-à-dire:

(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)

Finalement:

V = -3 V1 + 4 V2 + 0 V3

Nous concluons que V1, v2, v3 Ils forment une base dans l'espace vectoriel r³ de dimension 3.

-Exercice 2

Polynomial express p (t) = t² + 4T -3 comme combinaison linéaire de p1 (t) = t² -2t + 5, p2 (t) = 2t² -3t et p3 (t) = t + 3.

Solution

P (t) = x p1 (t) + et p2 (t) + z p3 (t)

où les nombres x, y, z doivent être déterminés.

En multipliant et en regroupant les termes avec le même degré en T, il est obtenu:

T² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)

Ce qui nous conduit au système d'équations suivant:

x + 2y = 1

-2x -3y + z = 4

5x + 3z = -3

Les solutions de ce système d'équations sont:

x = -3, y = 2, z = 4.

C'est-à-dire:

P (t) = -3 p1 (t) + 2 p2 (t) + 4 p3 (t)

-Exercice 3

Montrer que les vecteurs V1= (1, 0, -1, 2); V2= (1, 1, 0, 1) et V3= (2, 1, -1, 1) de R⁴ sont linéairement indépendants.

Solution

Nous combinons linéairement les trois vecteurs V1, V2, V3 Et nous exigeons que la combinaison ajoute l'élément nul de R⁴

pour V1 + b V2 + c V3 = 0

C'est-à-dire,

A (1, 0, -1, 2) + b (1, 1, 0, 1) + c (2, 1, -1, 1) = (0, 0, 0, 0)

Cela nous amène au système d'équations suivant:

A + B + 2 C = 0

B + c = 0

-A - C = 0

2 a + b + c = 0

Soustraire le premier et le quatrième que nous avons: -a + c = 0 ce qui implique a = c.

Mais si nous regardons la troisième équation, nous devons = -c. La seule façon de respecter a = c = (-c) est que C est 0 et sera donc également 0.

A = c = 0

Si nous remplaçons ce résultat dans la première équation, nous concluons que b = 0.

Enfin A = B = C = 0, il peut donc être conclu que les vecteurs V1, V2 et V3 sont linéairement indépendants.

Les références

1. Lipschutz, s. 1993. Algèbre linéaire. Deuxième édition. McGraw - colline. 167 - 198.