Formule et équations Effort de tension, calcul, exercices

Il Tension de contrainte Il est défini comme la force perpendiculaire à la zone par unité de zone appliquée à un objet à ses extrémités pour exercer sa traction, grâce à laquelle il allonge. Ses dimensions sont de force / zone et sous forme mathématique, nous pouvons l'exprimer comme suit:

τ = f / a

L'unité de l'effort dans le système international des unités est la même que celle utilisée pour la pression: la PA de Pascal, abrégée, qui équivaut à 1 Newton / m².

Figure 1. Si l'effort de tension dépasse une certaine valeur, la corde est brisée. Source: pxhere.

Dans l'effort de tension, il y a deux forces qui s'appliquent dans la même direction et les sens opposés, qui étirent le corps. Si à l'origine la longueur de l'objet était L_soit, Lors de l'application de l'effort de tension, la nouvelle longueur est L et l'étirement ΔL est calculé par:

Δl = l - l_soit

Les objets solides ont une élasticité dans une plus ou moins loin, ce qui signifie que lorsque l'effort de tension disparaît, ils reviennent à leurs dimensions d'origine.

Cela se produit à condition que l'effort ne soit pas si important pour provoquer une déformation permanente. Les matériaux en caoutchouc, en caoutchouc ou en caoutchouc sont bons pour les objets élastiques et ont également ces cheveux et la peau de qualité, entre autres.

[TOC]

Déformation unitaire

Lorsque vous étudiez comment les corps se déforment sous tension, il est très pratique de définir le concept de Déformation unitaire, Une quantité déclenchée. La déformation unitaire est indiquée par la lettre grecque Δ (minuscule "delta") et est calculée comme suit:

δ = Δl / L_soit

La déformation unitaire sert à évaluer relativement la déformation de l'objet sous tension. Voyons-le de cette manière: il n'est pas la même que d'étirer 1 cm par barre de 1 mètre de long, pour étirer 1 cm à 10 m de long. Dans le premier cas, la déformation est beaucoup plus importante que dans la seconde.

Il peut vous servir: ohm: mesures de résistance, exemples et exercice résolus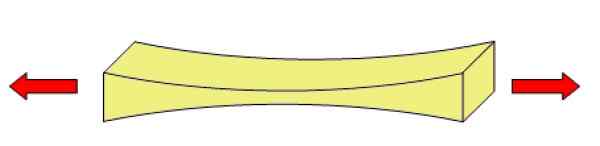Figure 2. Un objet subissant un effort de tension ou de traction est déformé. Source: Wikimedia Commons.

Comment l'effort de tension est-il calculé? (Exemples)

Le physicien anglais et contemporain de Newton nommé Robert Hooke (1635-1703), a étudié les propriétés élastiques des corps et a établi la loi qui porte son nom. Avec lui, l'effort appliqué à la déformation connue lorsque l'effort est petit est lié:

Effort ∝ déformation (unital)

Il est logique de s'attendre à ce que plus l'effort de stress soit important, un plus grand allongement se produira. Utilisation des définitions ci-dessus:

τ ∝ δ

La constante de proportionnalité nécessaire pour établir l'égalité est indiquée et est connue sous le nom de module jeune ou module d'élasticité, caractéristique des matériaux:

τ = y⋅δ

Le module de Young a les mêmes unités d'effort de tension, car la déformation unitaire est sans dimension.

Ainsi, un moyen de calculer l'effort de contrainte dans un corps aux propriétés élastiques, est de mesurer la déformation et de connaître son jeune module. Ce montant a été déterminé expérimentalement pour de nombreux matériaux et est tabulé.

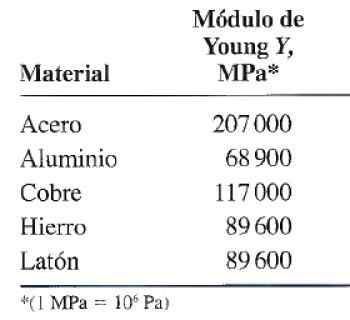figure 3. Tableau de module d'élasticité ou de module de Young pour certains matériaux à usage courant. Source: Valera Negrete, J. 2005. Notes de physique générale. Unam.

Exemple de calcul

Supposons qu'un acier trempé de 3 mm de diamètre soit soumis à un effort de tension, suspendu à un poids de 250 N, quelle serait l'ampleur de cet effort?

Eh bien, nous pouvons utiliser la définition de l'effort de tension comme quotient entre la force perpendiculaire à la surface et la zone de ladite surface. Calculons d'abord la zone, en supposant un fil de section croisée circulaire:

Il peut vous servir: numéro de masse: qu'est-ce que c'est et comment l'obtenir (avec des exemples)

A = π . (D / 2)² =  π . (d² / 4)

Le diamètre du fil est de 3 mm et ces unités doivent être transformées en mètres:

D = 3 x 10^-3 m.

A = π . (3 x 10^-3 m)² / 4 = 7.07 x 10^-6 m².

L'effort de tension est produit par le poids qui pend au fil, qui est appliqué perpendiculaire à sa section transversale, donc:

τ = 250 n / 7.07 x 10^-6 m² = 3.5 x 10 ⁷ Pennsylvanie

La Pascal est une unité assez petite, donc les multiples ne sont pas inhabituels. Sachant que 1 méga-Pascal (MPA) a 10 ans⁶ Pascal, l'effort de tension reste:

τ = 35 MPa

Exercices résolus

- Exercice 1

Le module d'élasticité d'une tige est 4 x 10^onze Pennsylvanie. Quelle déformation unitaire est obtenue en appliquant un effort de tension de 420 MPa?

Solution

L'équation à utiliser est:

τ = y⋅δ

Avec lui, nous calculons la déformation unitaire:

δ = τ / y = 420 x 10⁶ PA / 4 x 10^onze Pa = 0.00105

δ = Δl / L_soit

Par conséquent, la déformation ΔL est:

Δl = 0.00105 L_soit

Si, par exemple, la tige mesurait à l'origine 1 mètre de long, avec cet effort de tension, il étire seulement 0.00105 M = 1.05 mm.

- Exercice 2

Un fil en acier a 1.50 m de long et un diamètre de 0.400 mm. L'une des extrémités est attachée au toit et un réflecteur de masse est placé sur l'autre m = 1.50 kg, qui est libéré. Calculer:

a).

b) déformation unitaire et pourcentage de déformation unitaire. Est-il possible que le fil soit brisé par le poids du réflecteur?

Solution

Le fil va s'étirer, car le réflecteur est soumis à un effort de tension. La force produite par cet effort est le poids du réflecteur.

Il peut vous servir: physique avant les Grecs (Grèce Antigua)

Le poids d'un objet de masse est le produit de la masse par la valeur de l'accélération de la gravité: par conséquent:

F = 1.50 kg x 9.8 m / s² = 14.7 N

La section croisée de la section de fil est nécessaire:

A =  π . (d² / 4) = π x (0.4 x 10-3 m) 2/4 = 1.26 x 10^-7 m².

Avec ces résultats, l'effort exercé sur le fil est calculé:

τ = 14.7 n / 1.26 x 10^-7 m² = 1.17 x 10⁸ Pennsylvanie

Le fil a un comportement élastique, il est donc valable de supposer que la loi de Hooke est remplie:

τ = y⋅δ

À partir de la table du module d'élasticité, nous constatons que pour l'acier y = 207 x 10⁹ Pennsylvanie. De plus, la déformation unitaire est:

δ = Δl / L_soit

Remplacer dans l'équation pour l'effort:

τ = y⋅δ = y⋅ (Δl / L_soit)

Par conséquent, l'étirement est:

Δl = L_soit τ / y =

= 1.50 m x 1.17 x 10⁸ PA / 207 x 10⁹ Pa = 8.5 x 10^-4 m = 0.849 mm.

La déformation unitaire du fil est:

δ = Δl / L_soit = 8.5 x 10^-4 m / 1.5 m = 5.652 x 10^-4

Si nous l'exprimons en pourcentage, le pourcentage de déformation unitaire est 0.0565%, moins de 0.1%, il est donc prévu que le fil résiste au poids du réflecteur sans se casser, car la déformation qu'il éprouve n'est pas trop grande par rapport à la longueur d'origine.

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
2. Bière, f. 2010. Mécanique des matériaux. McGraw Hill. 5e. Édition.
3. Giancoli, D.  2006. Physique: principes avec applications. 6e. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1.
5. Valera Negrete, J. 2005. Notes de physique générale. Unam.