Formules d'équilibrage en rotation et équations, exemples, exercices

On prétend qu'un corps étendu est équilibre de rotation Lorsque la somme des couples qui agissent est nul. Cela ne signifie pas que l'objet est nécessairement au repos, mais plutôt qu'il n'y a pas de tendance nette à changer son état de mouvement vers un autre.

Un objet qui se déplace à une vitesse constante le fait le long d'une ligne droite et nous pouvons le considérer dans l'équilibre de la rotation. Maintenant, les objets tournent parce qu'il y a des forces qui agissent sur eux de telle manière que c'est une rotation. La capacité d'une force à produire une rotation, appelée couple ou Torca, Cela dépend non seulement de l'intensité de la force, mais aussi de son application.

Figure 1. Le pont de suspension de la figure a été conçu pour être en équilibre de rotation. Source: Wikimedia Commons.

Nous le reconnaissons immédiatement lorsqu'une porte fermée va s'ouvrir: la force n'est jamais appliquée près des charnières, mais loin d'eux, donc la poignée est placée aussi loin que possible, à côté de la porte de la porte.

Les charnières passent l'axe de rotation de la porte. Insistant pour le pousser très près des charnières, vous devez faire un gros effort pour que la porte se déplace même un peu.

Dans la littérature est le couple avec des noms différents: moment de torsion, torsion, moment de force et torca. Tous sont synonymes.

Nous devons donc connaître les couples qui agissent sur un objet pour établir la condition de bilan de rotation.

[TOC]

Condition du bilan de rotation

La condition de bilan de rotation est:

La somme de tous les moments ou couples qui agissent sur un corps, calculé par rapport à tout axe, doit être vide.

L'objet en question doit être étendu, car les particules, par définition, n'ont que l'équilibre de traduction.

Vous pouvez vous servir: la deuxième loi de Newton: applications, expériences et exercices

Il peut y avoir des forces appliquées sur le corps et il y a toujours un équilibre en rotation, tandis que les forces ne le tournent pas.

Il peut également y avoir du mouvement, même accéléré, mais toujours le long d'une ligne droite, car toutes les forces ne provoquent pas l'apparence de couples. Ceux-ci apparaissent lorsque les forces n'agissent pas tout au long de la même ligne d'action.

Couple ou moment de force

Le couple est indiqué avec les paroles grecques τ, dans caractère gras Parce que c'est un vecteur et nous le distinguons de sa magnitude ou de son module, qui est un scalaire. Cela dépend de la force appliquée F, du vecteur r qui est dirigé à partir de l'axe de rotation ou au point d'application de la force et enfin, de l'angle entre ces deux vecteurs.

La bonne relation entre ces amplitudes est établie à travers le produit vectoriel:

τ = r X F

Et le module de couple, désigné sans gras est:

τ = r⋅f⋅ssen θ

Où θ est l'angle entre r et F. Les unités de couple sont tout simplement n⋅m dans le système international.

Dans la figure, il y a une clé anglaise avec laquelle il est prévu. Pour cela, deux forces sont essayées F_POUR et F_B.

F_POUR est plus proche de O et a un vecteur r_POUR ou le bras de levier plus court, ne produit donc pas autant de couple et de force F_B, Cela a la même ampleur, mais il a un vecteur r_B plus grand.

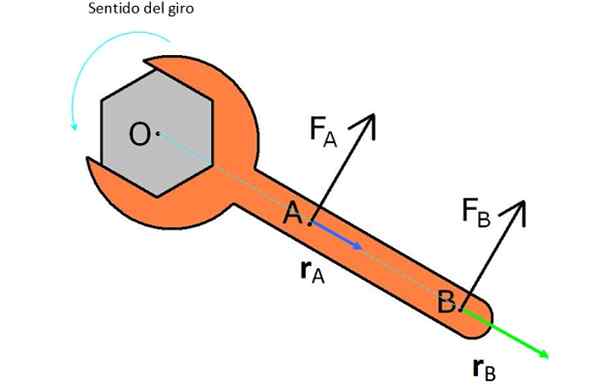Figure 2. Les forces et les bras appliqués à une clé anglaise pour le tourner contraire aux aiguilles d'horloge. Source: Wikimedia Commons.

Notez que si vous souhaitez faire pivoter l'écrou dans un horaire, vous devez appliquer les forces dans la direction opposée à la façon dont ils apparaissent sur la figure.

Direction et sens du couple

Comme le couple résulte du produit croisé entre les vecteurs de résistance et de position, et ceux-ci sont dans le plan de la clé anglaise, le couple doit être un vecteur perpendiculaire à ce plan, c'est-à-dire dirigé vers le lecteur ou à l'intérieur de la page.

Peut vous servir: pression atmosphérique: valeur normale, comment elle est mesurée, exemples

Par convention, le couple est positif s'il produit un tour dans la direction opposée des aiguilles de l'horloge, et négative s'il le fait en direction de l'horloge.

La direction et la direction du couple résultant sont facilement déterminées par la règle de la main droite illustrée ci-dessous:

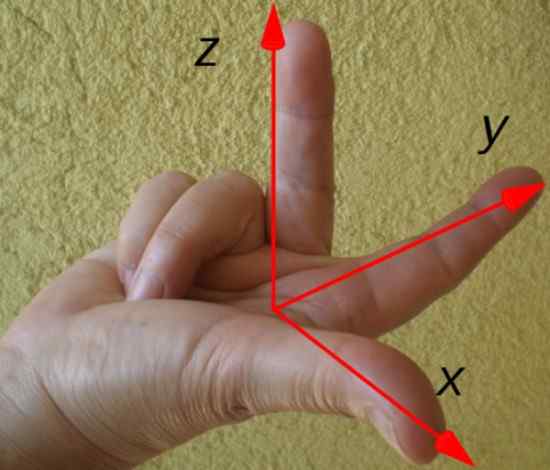figure 3. Règle de droite pour déterminer la direction et la direction du Troca. Source: Wikimedia Commons.

Les points d'index en fonction du vecteur de position r, Le majeur selon la force F Et le pouce signale la direction et la direction du couple τ. Dans cet exemple, le couple est dirigé le long de l'axe x, selon le dessin des axes de coordonnées.

Formules et équations

Si les couples agissent sur un corps τ₁, τ_2, τ_3… τ_Toi, Le filet ou le couple résultant τ_n C'est la somme vectorielle de tous:

τ_n = τ₁+ τ₂ +  τ₃ +_.. τ_Toi

Avec sommation de la sommation, il reste:

τ_n = ∑ τ_Toi

La condition d'équilibre s'exprime mathématiquement comme suit:

τ_n = 0

Ou bien:

∑ τ_Toi = 0

Où le couple τ, En ce qui concerne un certain axe O, il est calculé par:

τ = r X F

Et dont l'ampleur est:

τ = r⋅f⋅ssen θ

Exemples

-Chez l'homme et les animaux, le poids est une force qui peut provoquer un couple et tourner et tomber.

Les gens maintiennent généralement une telle position que lors de la marche, les maintient dans l'équilibre de la rotation, à moins que l'activité sportive ne soit pratiquée, comme la gymnastique, le patinage ou les sports en général.

-Deux enfants qui ont réussi à rester horizontal dans le bascule soit monte et descend Ils sont en rotation l'équilibre.

-Lorsque les soucoupes de l'équilibre sont équilibrées, le système est en équilibre de rotation.

-Les avis et les feux de circulation qui pendent dans les rues et les avenues sont également dans l'équilibre rotationnel. Si les câbles qui les maintiennent sont brisés, cet équilibre est perdu et que l'avis est suspendu ou tombe.

Il peut vous servir: Accélération moyenne: comment il est calculé et résolu

-Des ponts suspendus tels que Golden Gate à San Francisco et le pont de la figure 1.

Exercice résolu

La barre prise en charge par un support illustré sur la figure est très légère. La force exercée par le soutien est F Et à la fin, la force s'applique POUR.

Il est invité à calculer les amplitudes de ces forces étant donné que le système est en équilibre de traduction et de rotation.

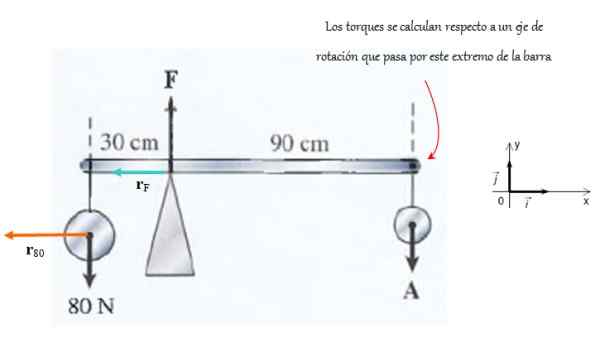Figure 4. Sur cette barre, les forces agissent de manière à ce qu'elle reste dans l'équilibre rotationnel. Source: F. Zapata.

Solution

Comme le système ne bouge pas, la somme des forces est annulée. Tous sont verticaux et vous pouvez travailler avec les amplitudes. Le sens positif est en hausse et le négatif en baisse: par conséquent:

F - 80 - a = 0

Maintenant, l'état d'équilibre de rotation est appliqué, pour lequel vous devez choisir un axe de rotation arbitraire. Dans ce cas, il est choisi à la fin à droite, de sorte que le vecteur r_POUR Être nul, de cette manière le couple exercé par POUR, mais seulement ceux de F Et la force de la gauche.

Le couple produit par F C'est, selon la règle de la main droite et le système de coordonnées indiqué:

τ_F = r_F X F = 0.9 F (-k) N.m

Il est réalisé à l'écran et a un signe négatif. Tandis que le couple produit par la force de 80 N est:

τ = 80 x 1.vingt (k) N⋅m = 96 (k) N⋅m

Ce couple est dirigé hors de l'écran et se voit attribuer un signe positif. Comme il y a l'équilibre rotationnel:

96 - 0.9⋅f = 0

L'ampleur de F est:

F = (96/0.9) n = 106.7 N

Et puisque le système est en solde de traduction, la somme des forces est annulée. Cela nous permet de nettoyer l'ampleur de POUR:

F - a - 80 n = 0

Donc:

A = 106.7 - 80 n = 26.7 N.

Les références

1. Rex, un. 2011. Fondamentaux de la physique. Pearson.
2. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Élégant. Cengage Learning.
3. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1. Pearson.
4. Tipler, P. (2006) Physique de science et de technologie. 5e ed. Volume 1. Éditorial Revered.
5. Tippens, P. 2011. Physique: concepts et applications. 7e édition. McGraw Hill.