Formules d'énergie gravitationnelles, caractéristiques, applications, exercices

La Énergie gravitationnelle C'est celui qui a un objet massif lorsqu'il est immergé dans le champ gravitationnel produit par un autre. Certains exemples d'objets avec de l'énergie gravitationnelle sont: la pomme dans l'arbre, la pomme tombant, la lune en orbite autour de la terre et de la terre en orbite autour du soleil.

Isaac Newton (1642-1727) a été le premier à réaliser que la gravité est un phénomène universel et que chaque objet avec masse produit dans son environnement un champ capable de produire une force sur une autre.

Figure 1. La lune en orbite autour de la terre a une énergie gravitationnelle. Source: Pixabay

[TOC]

Formules et équations

La force mentionnée à Newton est connue sous le nom de force gravitationnelle et fournit de l'énergie à l'objet sur lequel il agit. Newton a formulé la loi universelle sur la gravitation comme suit:

"Soyez deux objets de masse spécifiques M1 et M2 respectivement, chacun exerce sur l'autre une force d'attraction qui est proportionnelle au produit de leurs masses et inversement proportionnelle au carré de la distance qui les sépare.".

Dans l'expression précédente, F C'est la force de l'attraction gravitationnelle que l'objet 1 exerce sur l'objet 2 (ou vice versa), M1 et M2 Les masses respectives d'objets et r est la distance qui sépare les objets. g C'est une constante de proportionnalité connue sous le nom de constante gravitationnelle.

Énergie gravitationnelle OU associé à la force gravitationnelle F est:

Notez la présence d'un signe négatif, ce qui signifie que si la séparation entre les objets est finie, son énergie gravitationnelle est négative. Mais si la séparation tend à l'infini, alors l'énergie gravitationnelle est nulle.

Un objet immergé dans un champ gravitationnel a une énergie potentielle gravitationnelle OU et énergie cinétique K. S'il n'y a pas d'autres interactions, ou si elles sont d'une intensité négligeable, l'énergie totale ET De cet objet est la somme de son énergie gravitationnelle plus son énergie cinétique:

E = k + u

Si un objet est dans un champ gravitationnel et que d'autres forces dissipatives ne sont pas présentes, comme la friction ou la résistance à l'air, alors l'énergie totale ET C'est une quantité qui reste constante pendant le mouvement.

Caractéristiques de l'énergie gravitationnelle

- Un objet a une énergie potentielle gravitationnelle si elle n'est qu'en présence du champ gravitationnel produit par un autre.

- L'énergie gravitationnelle entre deux objets se développe à mesure que la distance de séparation entre eux est plus grande.

- Le travail effectué par la force gravitationnelle est égal et contraire à la variation de l'énergie gravitationnelle de la position finale par rapport à celle de sa position initiale.

Il peut vous servir: quel est l'équilibre de la particule? (Avec des exemples)

- Si un corps n'est soumis qu'à l'action de la gravité, alors la variation de son énergie gravitationnelle est égale et contraire à la variation de son énergie cinétique.

- L'énergie potentielle d'un objet de masse m à la hauteur H Concernant la surface de la Terre est MGH temps supérieur à l'énergie potentielle à la surface, étant g l'accélération de la gravité, pour les hauteurs H Beaucoup plus bas que le rayon terrestre.

Champ de champ et de gravitation

Le champ gravitationnel g Il est défini comme une force gravitationnelle F par unité de masse. Il est déterminé en plaçant une particule d'essai à chaque point de l'espace et en calculant le quotient entre la force qui agit sur la particule de test divisée par la valeur de sa masse:

g = F / m

Le potentiel gravitationnel v d'un objet de masse m comme l'énergie potentielle gravitationnelle de cet objet divisé par sa propre masse est définie.

L'avantage de cette définition est que le potentiel gravitationnel ne dépend que du champ gravitationnel, de sorte qu'une fois le potentiel connu V, Énergie gravitationnelle OU d'un objet de masse m est:

U = m.V 

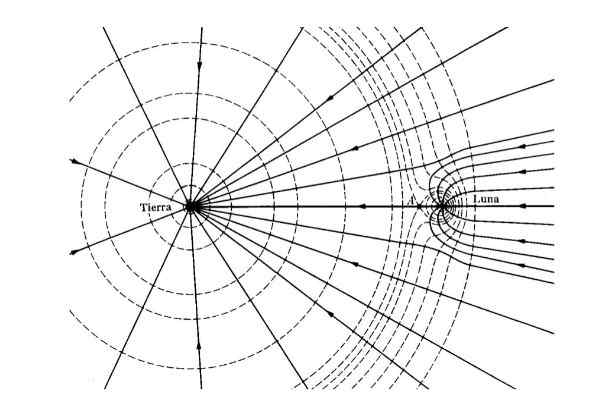Figure 2. Champ gravitationnel (lignes continues) et Equi-potentiel (ligne segmentée) pour le système terrestre - Luna. Source: W T Scott, Am. J. Chèque. 33, (1965).

Applications

L'énergie potentielle gravitationnelle est ce que les corps stockent lorsqu'ils sont dans un champ gravitationnel.

Par exemple, l'eau contenue dans un réservoir a plus d'énergie dans la mesure où le réservoir est plus élevée.

À un réservoir plus élevé, plus la vitesse de sortie de l'eau est élevée par le robinet. En effet.

Lorsque l'eau est endommagée au sommet d'une montagne, cette énergie potentielle peut être utilisée pour faire tourner les turbines de production d'électricité.

L'énergie gravitationnelle explique également les marées. Comme l'énergie et la force gravitationnelle dépendent de la distance, l'attraction gravitationnelle de la lune est plus grande face à la terre la plus proche de la lune que le visage le plus éloigné et le plus opposé.

Cela produit une différence de forces qui déforment la surface de la mer. L'effet est plus grand sur une nouvelle lune, lorsque le soleil et la lune sont alignés.

La possibilité de construire des stations spatiales et satellites qui restent relativement proches de notre planète, est due à l'énergie gravitationnelle produite par la Terre. Sinon, les stations spatiales et les satellites artificiels se promener dans l'espace.

Il peut vous servir: Imantation: ce qui consiste, la méthode et les exemples

Potentiel gravitationnel de la terre

Supposons que la terre a la masse M et un objet qui est au-dessus de la surface de la Terre à distance r En ce qui concerne le centre de la même m. 

Dans ce cas, le potentiel gravitationnel est déterminé à partir de l'énergie gravitationnelle se séparant simplement entre la masse de l'objet résultant:

Le potentiel gravitationnel à la surface de la Terre est obtenu en remplaçant r Par le rayon terrestre r_T. 

Énergie potentielle près de la surface de la Terre

Supposons que la Terre ait la radio R_T  et la masse M.

Même si la Terre n'est pas un objet opportun, le champ à sa surface équivaut à ce qui serait obtenu si toute sa masse M Il était concentré au centre, de sorte que l'énergie gravitationnelle d'un objet en hauteur H à la surface de la Terre est 

U (r_T + H) = -G.M m (r_T + h) ^ - 1

Mais parce que h est bien inférieur à r_T, L'expression précédente peut s'approcher de 

U = uo + mgh

Où g est l'accélération de la gravité, dont la valeur moyenne pour la Terre est de 9.81 m / s ^ 2.

Ensuite, l'EP d'énergie potentielle d'une masse m à la hauteur H à la surface de la Terre est:

Ep (h) = u + uo = mgh

Sur la surface de la Terre H = 0, donc un objet à la surface a EP = 0. Des calculs détaillés peuvent être vus sur la figure 3.

figure 3. Énergie potentielle gravitationnelle à une hauteur H à la surface. Source: Préparé par F. Zapata.

Exercices 

Exercice 1: effondrement de la terre gravitationnelle

Supposons que notre planète subit un effondrement gravitationnel pour la perte d'énergie thermique à l'intérieur et son rayon se désintègre jusqu'à la moitié de la valeur actuelle mais la masse de la planète est constante.

Déterminez ce qui serait l'accélération de la gravité près de la surface de la nouvelle terre et combien un survivant pesant 50 kg-F avant l'effondrement. Augmente ou diminue l'énergie gravitationnelle de la personne et dans quel facteur.

Solution

L'accélération de la gravité à la surface d'une planète dépend de sa masse et de son rayon. La constante de gravitation est universelle et sert également pour les planètes et les exoplanètes.

Dans le cas où nous sommes élevés, si le rayon de la terre est réduit de moitié, l'accélération de la gravité de la nouvelle terre serait 4 fois supérieure. Les détails peuvent être vus sur la prochaine planche.

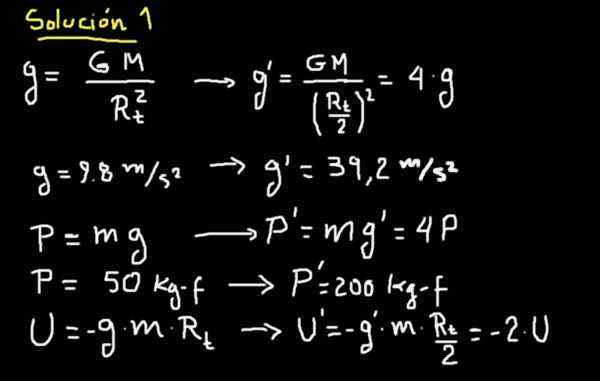
Cela signifie qu'un superman et un survivant qui sur la vieille planète pesaient 50 kg-F pèseront 200 kg-f sur la nouvelle planète.

Peut vous servir: équilibre thermique: équations, applications, exercices

D'un autre côté, l'énergie gravitationnelle aura été réduite de moitié à la surface de la nouvelle planète.

Exercice 2: effondrement gravitationnel et vitesse d'échappement

En référence à la situation soulevée dans l'exercice 1, ce qui arriverait à la vitesse d'échappement: augmente, diminue, dans quel facteur?

Solution 2

La vitesse d'échappement est la vitesse minimale nécessaire pour échapper à l'attraction gravitationnelle d'une planète.

Pour le calculer, il est supposé qu'un projectile qui tire avec cette vitesse atteint l'infini avec une vitesse zéro. De plus, dans l'infini l'énergie gravitationnelle est nul. Par conséquent, un projectile qui tire avec la vitesse d'échappement n'aura aucune énergie totale.

C'est-à-dire qu'à la surface de la planète au moment du tir, la somme de l'énergie cinétique de l'énergie de projectile + gravitationnelle doit être vide:

½ m ve ^ 2 - (g m.M_T = 0

Notez que la vitesse d'échappement ne dépend pas de la pâte du projectile et de sa valeur carrée est

Ve ^ 2 = (2g m) / r_T

Si la planète s'effondre jusqu'à un rayon la moitié de l'original, le carré de la nouvelle vitesse d'échappement devient double.

Par conséquent, la nouvelle vitesse d'échappement se développe et devient 1.41 fois l'ancienne vitesse d'évasion:

Ve '= 1.41 Voir

Exercice 3: Énergie gravitationnelle des pommes

Un garçon sur le balcon d'un bâtiment à 30 mètres du sol libère une pomme de 250 g, ce qui, après quelques secondes, atteint le sol.

Figure 4. En chute, l'énergie potentielle de la pomme se transforme en énergie cinétique. Source: Pixabay.

a) Quelle est la différence d'énergie gravitationnelle de la pomme au sommet de la pomme au niveau du sol?

b) À quelle vitesse la pomme a-t-elle été à la propagation du sol?

c) Qu'en est-il de l'énergie une fois que la pomme s'est écrasée contre le sol? 

Solution

a) La différence d'énergie gravitationnelle est 

m.g.H = 0.250 kg * 9.81 m / s ^ 2 * 30 m = 73.6 J

b) L'énergie potentielle que la pomme avait quand elle mesurait 30 m de haut est transformée en énergie cinétique lorsque la pomme atteint le sol.

½ m v ^ 2 = m.g.H

V ^ 2 = 2.g.H

En remplaçant les valeurs et la compensation, il s'ensuit que la pomme atteint le sol avec une vitesse de 24.3 m / s = 87.3 km / h.

c) De toute évidence, la pomme est dispersée et toute l'énergie gravitationnelle accumulée au début est perdue sous forme de chaleur, car les pièces de pomme et la zone d'impact sont chauffées, en plus une partie de l'énergie est également dissipée sous la forme d'ondes sonores "Splash".

Les références

1. Alonso, m. (1970). Vol Physique. 1, Fonds éducatif inter-américain. 
2. Hewitt, Paul. 2012. Sciences physiques conceptuelles. 5e. Élégant. Pearson.
3. Chevalier, r. 2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique. Pearson.
4. Sears, f. (2009).University Physics Vol. 1 
5. Wikipédia. Énergie gravitationnelle. Récupéré de: est.Wikipédia.com
6. Wikipédia. Énergie gravitationnelle. Récupéré de: dans.Wikipédia.com