Dans quelles situations sont des fonctions linéaires et quadratiques?

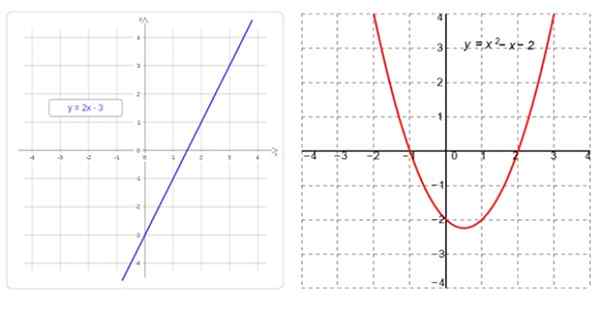
À gauche une fonction linéaire, dont le graphique est une ligne droite, et à droite, une fonction quadratique, dont le graphique est une parabole. Source: F. Zapata

Quelles sont les fonctions linéaires et quadratiques?

Les fonctions linéaires et les fonctions quadratiques sont des fonctions qui appartiennent au groupe des fonctions polynomiques. Ils sont utilisés pour modéliser diverses situations, telles que la dépendance entre le volume et le poids d'un corps, la quantité et le coût d'un produit, la position par rapport au temps et plus.

En général, une fonction est une relation qui relie deux variables et peut être utilisée pour modéliser le monde réel. Les fonctions polynomiques, comme son nom l'indique, sont exprimées par un polynôme, dont la forme générale est:

f (x) = a_nXⁿ + pour _N-1X ^N-1 + pour_X-2X^N-2 +… pour_soit

Où n est un nombre naturel, les nombres à₀, pour₁, pour₂,… pour_n Ils sont réels, pour₀ C'est le terme indépendant et pour_n, C'est le coefficient qui accompagne la plus grande puissance. La valeur de n indique le type de fonction, pour n = 1 la fonction est linéaire, tandis que pour n = 2 la fonction est quadratique.

Dans le premier de ces cas, l'expression générale est réduite à:

f (x) = a₁x + a_soit

Et dans le deuxième cas, il reste comme ceci:

f (x) = a₂X² + pour₁x + a_soit ;   (pour₂≠ 0)

Les graphiques des fonctions polynomiales sont continue, c'est-à-dire qu'ils ne subissent pas de sauts ou de ruptures brusques, ayant ainsi un comportement doux, sans irrégularités. Par conséquent, ils sont observés dans la modélisation de nombreuses situations de la science, de l'économie et d'autres domaines de la connaissance humaine.

Ensuite, des applications intéressantes les unes des autres sont décrites plus en détail.

Les situations dans lesquelles les fonctions linéaires apparaissent

La fonction linéaire est représentée algébriquement par:

f (x) = a₁x + a_soit

Ou équivalent:

f (x) = mx + b

Sa caractéristique distinctive est que son graphique est une ligne droite. La valeur m, qui est le coefficient du X, représente le boucle d'oreille de cette ligne et donne une mesure de son incliné.

Peut vous servir: Programmation non linéaire: méthodes et exercices

La pente peut être positive, négative ou zéro, mais elle est toujours constante, c'est-à-dire que son taux de change reste inchangé.

Une ligne de pente 0 est totalement horizontale, celle de la pente positive indique une élévation ou une augmentation (si l'une des variables augmente, l'autre aussi, toujours au même rythme) et, enfin, la pente négative indique une diminution (comme une variable augmente, l'autre diminue).

La valeur de b, Pour sa part, il représente la coupe ou l'intersection de la ligne avec l'axe vertical. Ouais B = 0, La ligne passe par l'origine du système de coordonnées.

Modélisation des exemples avec des fonctions linéaires

1. Le mouvement rectiligne uniforme

L'équation qui relie la position X et le temps t d'un mobile, dans le mouvement rectiligne uniforme, est linéaire:

x (t) = v⋅t + x_soit

Où v, la pente de la ligne, est la vitesse du mobile, qui reste constante tout au long du mouvement, et x_soit est la position initiale.

2. Densité

Densité d'un objet ou d'une substance, qui établit la relation entre la masse et le volume. Appelant ρ à la densité (il lit "Rho"), M à la pâte et V au volume, vous avez:

Effacer la pâte, en termes de volume, il est obtenu:

M = ρv

Lors de la graphique de la pâte en fonction du volume, une ligne droite est obtenue dont la pente est la densité de l'objet ou de la substance.

3. Longueur d'une circonférence

Le contour d'un cercle, ou sa longueur, est proportionnel à son rayon. Cela signifie que plus le rayon est grand, plus la circonférence contourne est grande, selon l'équation:

Peut vous servir: coefficient de corrélation: formules, calcul, interprétation, exemple

C = 2πr

Où c est le contour ou la longueur, R est la radio et π (lit «pi») est une constante dont la valeur approximative est πamp3.14 ..

4. Coût de l'envoi d'un colis

Comme il est facile à déduire, le plus lourd ou le plus volumineux est un ensemble plus cher consiste à le transporter. Les entreprises qui se consacrent au transport de fret modélisent leurs prix à la suite de certaines règles, par exemple:

C (x) = 2.75x

Dans cette équation, C (x) est le coût en dollars pour envoyer un paquet dont le poids est x livres. La valeur constante 2.75 possède des unités de dollar / livre (coût unitaire).

Situations dans lesquelles apparaissent les fonctions quadratiques

Algébriquement, une fonction quadratique est représentée par:

f (x) = a₂ X² + pour₁ x + a_soit

Avec la condition que le coefficient pour₂ Être différent de 0. Il se caractérise par son graphique en forme de parabole, dont l'axe axial ou l'axe de symétrie est vertical (parallèle à l'axe y))).

L'intersection entre la parabole et ledit axe est un point appelé sommet. Si la parabole s'ouvre (un₂ > 0), le sommet est son point minimum, et s'il s'ouvre (un₂ < 0), es el máximo.

Sur l'axe de la symétrie est le foyer, un point spécial qui détermine la courbure de la parabole. Si la lumière du soleil est influencée sur un miroir parabolique, les rayons se refléteront sur la surface, coïncidant dans la focalisation, qui est chauffée immédiatement.

Modélisation des exemples avec des fonctions quadratiques

1. Hauteur d'un projectile lancé verticalement

Un projectile est tout objet auquel une vitesse initiale est fournie puis libérée, sous l'action de la gravité. Si la vitesse initiale est verticale, magnitude v₀ Et dirigé vers le haut, l'objet atteindra une hauteur maximale puis descendra.

Peut vous servir: homotecia

L'équation de la hauteur H en fonction du temps t est:

H (t) = −4.9 T²+V₀ t

Où le sens vertical est considéré comme positif, et le basse vertical négatif.

2. La trajectoire d'un projectile horizontal ou oblique

Si une vitesse initiale horizontale ou oblique est fournie à un projectile, il décrira une trajectoire parabolique, qui peut être représentée par une fonction quadratique comme décrit précédemment.

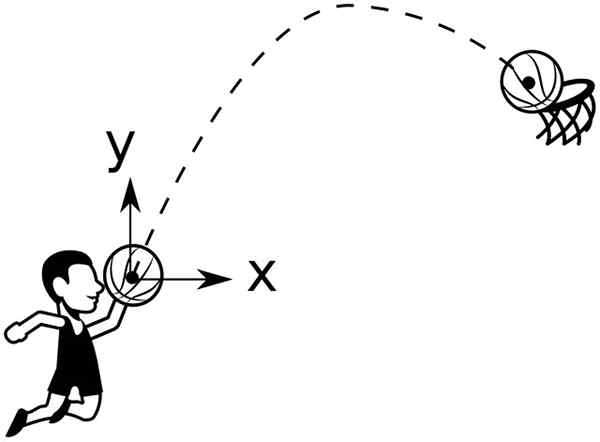La balle du panier décrit une trajectoire parabolique à jeter dans le panier. Source: Wikimedia Commons

Par exemple, une balle lancée d'une hauteur et₀, Angle de formation θ₀ En ce qui concerne l'horizontal, il a une trajectoire donnée par:

Avec g comme accélération de la gravité, qui peut se rapprocher de 10 m / s². Par exemple, un ballon de football se lance du sol (et₀ = 0), avec une vitesse initiale de 6 m / s et un angle de 45º par rapport à l'horizontal, aura une trajectoire donnée par la parabole suivante:

3. La zone d'un cercle

Plus le rayon du cercle est élevé, plus sa zone sera grande. En effet, la zone du cercle est proportionnelle au carré du rayon r, la constante de proportionnalité étant le nombre π:

A = πr²

4. Efficacité d'une publicité

Plus ils le voient, plus une annonce commerciale est efficace. Efficacité e, sur une échelle de 0 à 10, à partir d'un avis peut être modélisé en fonction de la fonction quadratique suivante:

Les références 

1. Fonctions polynomiques. Récupéré des ressources.éducation.est.
2. Larson, R. (2012). Précalation. 8e. édition. Cengage Learning.
3. Miller, C. (2013). Mathématiques: raisonnement et applications. 12e. édition. Pearson Education.
4. Stewart, J. (2012). Précalation. Mathématiques pour le calcul. 6e. édition. Cengage Learning.
5. Zill, D. (2008). Précculement avec avancées de calcul. 4e. édition. McGraw Hill.