Équations fractionnées
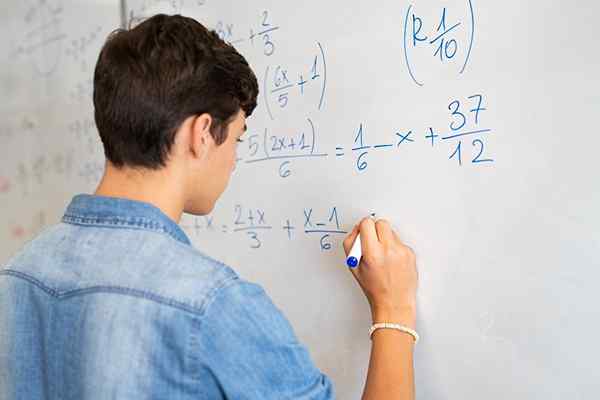
- 1410
- 131
- Prof Noah Collet
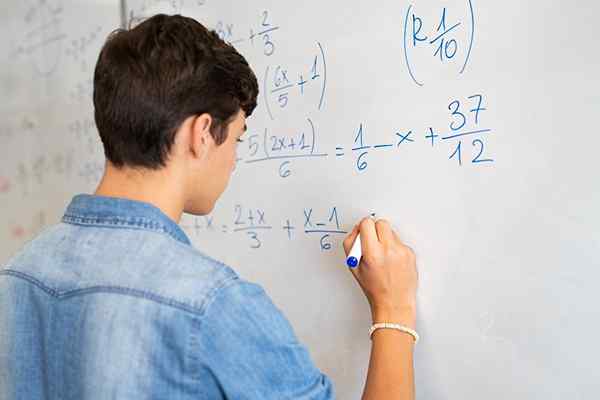 Les équations fractionnaires comprennent des fractions numériques et / ou algébriques, et l'inconnu peut être à la fois dans le numérateur et le dénominateur, ou les deux
Les équations fractionnaires comprennent des fractions numériques et / ou algébriques, et l'inconnu peut être à la fois dans le numérateur et le dénominateur, ou les deux Que sont les équations fractionnaires?
Le équations fractionnées sont ceux qui contiennent des fractions dans un ou plusieurs de leurs termes. De telles fractions peuvent être numériques ou algébriques, où l'inconnu peut être trouvé dans le numérateur et / ou dans le dénominateur de tout terme.
Ensuite, quelques exemples d'équations fractionnaires avec une seule inconnue:
Le premier exemple est une équation linéaire avec des coefficients fractionnaires; Dans le deuxième exemple, l'inconnu se trouve dans le dénominateur de chacun des termes, et dans le dernier, l'inconnu est à la fois le numérateur et dans le dénominateur.
Pour les résoudre, il est nécessaire d'effectuer des transformations algébriques et donc d'obtenir une équation équivalente, dans laquelle l'inconnu n'apparaît pas dans le dénominateur. Une fois cette procédure effectuée, la solution se trouve en utilisant les techniques appropriées.
La solution se compose de l'ensemble de valeurs «x» qui satisfont l'égalité. Cela peut être une valeur unique, ou plusieurs, mais, en tout cas, il est très important de garder à l'esprit que toutes les solutions de l'équation équivalente ne sont pas acceptables pour l'équation d'origine.
En effet, s'il s'agit d'une équation dont l'inconnu est dans le dénominateur, les valeurs «x» qui annulent, il doit être évité, même s'ils appartiennent à l'ensemble des solutions d'équation équivalentes. C'est parce que la division entre 0 n'est pas définie.
Si l'équation équivalente a une solution unique, et il s'avère que le dénominateur de l'une des termes de l'équation d'origine est annulée, alors elle n'a pas de solution.
Comment résoudre une équation fractionnaire
Les opérations qui sont effectuées pour résoudre les équations non fractionnelles sont valides, à condition que l'égalité soit maintenue. De cette façon, dans une équation fractionnaire, vous pouvez ajouter ou soustraire la même quantité aux deux côtés de l'égalité, multiplier tous les termes par la même quantité, ou diviser chaque terme par le même montant (différent de 0).
Peut vous servir: théorème de BolzanoMais comme l'équation fractionnaire est nécessaire pour se transformer en un autre équivalent sans dénominateurs, les indications générales suivantes sont également suivies:
- Trouvez le multiple commun minimum des dénominateurs (M.c.m).
- Multiplier chaque terme par le m.c.m., Afin d'éliminer les dénominateurs.
- Résoudre l'équation équivalente obtenue.
- Vérifiez que les solutions ont trouvé satisfaire l'égalité d'origine.
Types d'équations équivalentes
Les équations équivalentes obtenues à la suite de la procédure indiquée peuvent être:
- Linéaire ou au premier degré
- Quadratique
- D'ordre supérieur
Exemples résolus
Exemple 1
Résolvez l'équation suivante:
Il est à noter que l'équation est au premier degré en "x", car "x" est élevé à 1. Les coefficients de l'équation sont des fractions et un moyen de les éliminer, de travailler avec des nombres entiers, il multiplie tous les termes par le multiple minimum de dénominateurs (M.c.m.).
m.c.m. (2,3,6) = 6
Ensuite:
3x - 2x = 1
x = 1
Le lecteur peut vérifier la validité de cette solution, en remplaçant X = 1 dans l'équation d'origine et en vérifiant qu'une égalité est obtenue.
Exemple 2
Déterminez les valeurs «x» qui satisfont:
Contrairement à l'exemple précédent, dans ce cas, l'inconnu se trouve dans le dénominateur. Notez que les dénominateurs sont annulés pour les valeurs x = 2 et x = −1, un détail qui est pratique à prendre en compte, car, si l'équation équivalente admet ces solutions, nous devons les jeter, car ils ne sont pas admissibles Dans l'équation d'origine.
Maintenant, nous devons transformer l'équation en une autre sans dénominateurs, la première étape consiste à faire la somme des termes à gauche de l'égalité:
Comme les dénominateurs sont les mêmes, de sorte que l'égalité est remplie, il est nécessaire que les numérateurs soient également:
Peut vous servir: Constructions de proportionnalité: ce qui est, calcul, exercices4 (x + 1) - 3 (x -2) = 8
Il suffit de résoudre cette équation, qui se révèle être la première année:
4x + 4 - 3x + 6 = 8
x = 8 - 6 - 4 = - 2
x = - 2
Étant donné que cette valeur est différente des valeurs interdites, elle est admise comme une solution de l'équation d'origine.
Exemple 3
Trouvez la solution de:
Dans cette équation, la valeur x = 4 annule les dénominateurs, par conséquent, il est exclu de l'ensemble de solution de l'équation transformée, s'il apparaissait.
L'équation transformée est facile à trouver, il suffit de multiplier tous les termes par le facteur (X-4):
Rester:
2x - 4 = 4
2x = 8
x = 4
Exemple 4
Résous l'équation:
Dans ce cas, les dénominateurs ont des termes quadratiques, il est donc pratique de les prendre en compte d'abord:
- X2 + 8x + 7 = (x + 7) (x + 1)
- X2 - 49 = (x + 7) (x - 7)
- X2 - 6x - 7 = (x - 7) (x + 1)
L'équation est comme ceci:
Les valeurs de x qui annulent l'un des dénominateurs sont: x = −7, x = 7, x = −1. Par conséquent, même si ces valeurs font partie de l'ensemble de solution de l'équation modifiée, elles ne peuvent pas être une solution de l'équation d'origine.
Vient maintenant le processus de transformation de l'équation. La première étape consiste à trouver le multiple commun minimum des dénominateurs:
m.c.m. = (x + 7) (x - 7) (x + 1)
En multipliant des deux côtés de l'égalité par m.c.m. est laissé:
Résultant:
(x --7) (x− 2) = (x + 1) (2x - 5) - (x + 7) (x - 2)
Grâce à des biens distributifs, les produits sont développés:
X2 - 9x +14 = 2x2 - 3x - 5 - (x2 + 5x - 14)
Réduire des termes similaires sur le côté droit:
X2 - 9x + 14 = x2 - 8x + 9
Les termes quadratiques sont annulés, en rencontrant le même signe de différents côtés de l'égalité:
Peut vous servir: différence de cubes: formules, équations, exemples, exercices- 9x + 14 = - 8x + 9
-x = -5 ⇒ x = 5
Ce résultat est admis comme une solution, car ce n'est aucune des valeurs interdites.
Exercice d'application des équations fractionnaires
Le dénominateur d'une fraction dépasse quatre unités au numérateur. Si le numérateur est soustrait du numérateur et du dénominateur également, la fraction résultante est 3/5. Déterminez la fraction d'origine.
Solution
Soit x la valeur du numérateur.
Étant donné que le dénominateur de fraction dépasse quatre unités au numérateur, la fraction d'origine est:
Vous devez maintenant soustraire 5 unités, à la fois au numérateur et au dénominateur:
Étant donné que la fraction résultant de la réalisation de la procédure précédente est égale à 3/5, elles sont égalisées:
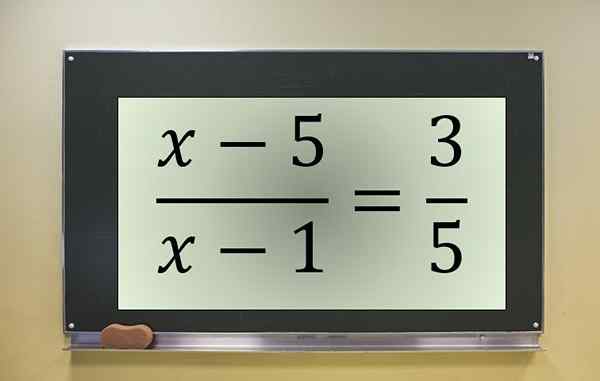 Exemple d'équation fractionnaire. Source: F. Zapata.
Exemple d'équation fractionnaire. Source: F. Zapata. Il s'agit d'une équation fractionnaire avec l'inconnu dans le numérateur et le dénominateur, qui est annulé à x = 1. Par conséquent, cette valeur doit être exclue s'il faisait partie des solutions de l'équation transformée.
Ensuite, il se multiplie les deux côtés par le multiple commun minimum, qui est 5 (x - 1):
Résultant en l'équation équivalente suivante:
5 (x - 5) = 3 (x - 1)
Application de biens distributifs:
5x -25 = 3x - 3 ⇒ 2x = 22
x = 11
La fraction d'origine remplace x = 11 dans l'expression:
Résultant en fraction 11/15. C'est la réponse au problème soulevé.
Les références
- Équations fractionnées. Récupéré de: Mathepower.com
- Portail de mathématiques. Équations fractionnées. Résolution des problèmes. Récupéré de: Silvioduarte.com.
- Stewart, J. (2007). Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
- Sullivan, m. (1997). Précalation. 4e. Édition. Pearson Education.
- Zill, D. (2008). Précculement avec avancées de calcul. 4e. Édition. McGraw Hill.



(x+1))

=6\left%20(%20\frac16%20\right%20))
-3(x-2)(x-2)(x+1)=\frac8(x-2)(x+1))
\left%20(%20\fracxx-4%20\right%20)+(x-4)=(x-4)\left%20(%20\frac4x-4%20\right%20))

(x+1)=\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1))
(x-7)(x+1)\left%20[%20\fracx-2(x+7)(x+1)%20\right%20]=(x+7)(x-7)(x+1)\left%20[%20\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1)%20\right%20])



\left%20(%20\fracx-5x-1%20\right%20)=5(x-1)\frac35)