Équation d'Arrhenius
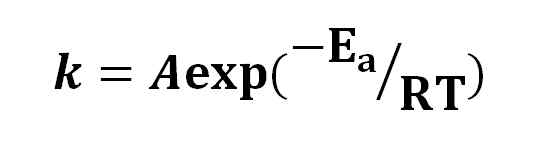
- 1923
- 84
- Prof Ines Gaillard
Quelle est l'équation d'Arrhenius?
La Équation d'Arrhenius C'est une approche qui relie la vitesse à la vitesse d'une réaction chimique en fonction de la température. Il a été créé en 1899 par le chimiste suédois Svante Arrhenius (1859-1927). Représente l'une des contributions les plus fondamentales dans le développement de la cinétique chimique.
Cette équation doit ses bases théoriques à de nombreux scientifiques, notamment Wihelmy (1850), Berthelot (1862) et J. J. Hood (1885). Mais la plus grande influence est attribuée à la création de l'équation d'Arrhenius au travail effectué par Van't Hoof (1884), qui a établi une dépendance aux constantes d'équilibre des réactions chimiques avec la température.
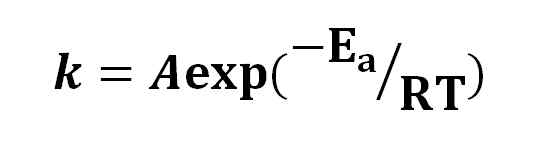 Équation d'Arrhenius. Source: Gabriel Bolívar.
Équation d'Arrhenius. Source: Gabriel Bolívar. Sur la base de l'équation d'Arrhenius, l'idée qu'une augmentation de 10 ºC a provoqué une duplication de la vitesse de réaction a été diffusée. D'autres interprétations qui le deviennent est que les molécules ont besoin d'une énergie d'activation pour réagir les unes aux autres.
De même, il est souligné que l'équation d'Arrhenius est une autre forme de désintégration exponentielle dans laquelle la valeur de la vitesse constante en fonction de l'exposant -epour/ Rt, où epour est l'énergie d'activation.
Équation et explication
L'équation d'Arrhenius a les deux expressions suivantes:
K = ae-EA / RT
Forme de l'équation utilisée en chimie et est liée à des moles de réactif.
K = ae-EA / KBT
Forme de l'équation utilisée en physique et est liée aux molécules plus que avec les taupes.
Les deux dérivent de l'équation de sabot Van´ pour la variation de la constante d'équilibre K en fonction de la température. L'équation de base est:
d (ln k) / dt = epour/ Rt2
Il peut vous servir: Dibenzalacetona: propriétés, mécanisme de réaction, utilisations, risquesQui est intégré en supposant quepour est indépendant de la température. Donc nous avons:
ln k = - epour/ Rt + ln a
Où ln a est la constante d'intégration. Lorsque la fonction exponentielle est appliquée des deux côtés de l'équation, nous obtenons l'équation d'Arrhenius déjà introduite.
Composants
k
C'est la vitesse constante d'une réaction chimique. Sa valeur peut être obtenue, en plus de l'utilisation de l'équation d'Arrhenius, par l'application de la loi de vitesse. Représente le nombre de collisions entre les particules produites par une réaction par seconde.
POUR
C'est le soi-disant facteur pré-exponentiel, qui représente la fréquence des collisions entre les molécules de réactif avec une orientation géométrique appropriée qui peut ou non produire une réaction chimique. Si la variation de la température est de peu d'ampleur, elle est généralement considérée comme constante. Ce facteur a sa propre formule:
A = z ρ
Où z est connu comme une fréquence ou un facteur de collision, et ρ le facteur géométrique ou stérique qui indique l'orientation relative des molécules au point de collision. La constante A a les mêmes unités que la vitesse de vitesse. Dans le cas où il n'y a pas d'énergie d'activation, l'ampleur de A sera égale à celle de k.
ETpour
C'est l'énergie d'activation, qui représente l'énergie seuil avant d'atteindre la statistique de transition.
L'énergie d'activation a l'unité KJ / MOL. Mais dans les calculs, la J / mol est utilisée comme unité. Le moins (-) signe qui précède le epour, Il sert à indiquer que son augmentation produit une diminution de la vitesse de réaction, ainsi que sa diminution produit une augmentation de la vitesse de réaction.
Peut vous servir: chromatographie en phase gazeuseRt
Représente l'énergie cinétique moyenne. Pendant ce temps, R est la constante universelle des gaz, étant l'une de ses valeurs les plus utilisées 8.31 J · K-1· Mol-1. Et t est la température absolue exprimée dans Kelvin (K).
et
C'est la base des logarithmes naturels ou néépériens, ayant une valeur de 2.71828.
et-EA / RT
C'est la fraction des molécules de réaction avec une énergie égale ou excessive par rapport à l'énergie d'activation.
Applications
La plupart des applications de l'équation d'Arrhenius proviennent de l'utilisation dans la détermination de la vitesse constante; et par extension, la vitesse de la réaction, ainsi que son énergie d'activation.
Par exemple, un modèle chimique a été développé sur la base de l'équation d'Arrhenius, qui peut prédire les propriétés des matériaux comme changement de température, appliqués dans les domaines de la géologie, de la construction, de l'ingénierie des matériaux et de la science alimentaire.
Il a été appliqué, bien qu'avec certaines critiques, l'équation d'Arrhenius dans la cinétique des réactions à l'état solide. Il a également été utilisé pour caractériser les réponses des plantes au stress hydrique.
L'équation Arenhius a servi de base à la création d'un modèle mathématique, qui quantifie l'effet de la température sur la durée de vie utile des cellules ou batteries hydrure métalliques nickel.
De même, sur la base de l'équation d'Arrhenius, le taux de décomposition des déchets de porcs et l'huile de cuisson ont été établies, sous divers contenus d'humidité.
Exercices résolus
Exercice 1
Quelle est l'énergie d'activation d'une réaction s'il est constaté que sa vitesse constante triples lorsque la température passe de 600 K à 610 K?
Peut vous servir: acide phénoxyacétique: synthèse, procédure, utilisations, risquesÀ partir de l'équation d'Arrhenius:
k = a · e-EA / RT
Nous effacons le facteur A:
A = k1 / (e-EA / RT1)
Mais puisque nous avons deux températures, t1 et T2, Il y aura deux constantes de vitesse: k1 et K2. Le facteur A ne change pas, nous pouvons donc le faire correspondre pour la deuxième température:
k1 / (e-EA / RT1) = k2 / (e-EA / RT2)
Et nettoyer Epour nous aurons:
ETpour = R (ln k2/ k1) / (1 / t1 - 1 / t2)
Comme quoi2 est trois fois plus grand que k1,
k2 / k1 = 3
ln (3) = 1.099
Et d'autre part:
1 / t1 = 1/600 K = 1.66 x 10-3 K-1
1 / t2 = 1/610 K = 1.64 x 10-3 K-1
Remplacement alors:
ETpour = (8.31 J · K-1· Mol-1) (1.099) / (1.66 x 10-3 K-1 - 1.64 x 10-3 K-1)
= 456.5 kJ · mol-1
Exercice 2
Dans une réaction en phase gazeuse, l'énergie d'activation est égale à 103 kJ / mol, et la constante de vitesse est 0.085 min-1. Calculez la vitesse constante à 323 K.
D'après l'expression précédente, nous effacons ln k2/ k1:
LN K2/ k1 = (Epour/ R) (1 / t1 - 1 / t2)
Développer la bonne partie de l'équation:
LN K2/ k1 = (103.000 j · mol-1 / 8.31 J · K-1· Mol-1) (1/273 K - 1/323 K)
LN K2/ k1 = 6.99
Prendre des antilogarithmes:
k2/ k1 = 1.086
k2 = (k1) (1.086)
= (0.085 min-1) (1.086)
= 0.092 min-1
Les références
- Whitten, Davis, Peck & Stanley. (2008). Chimie. (8e Ed.). Cengage Learning.
- Walter J. Moore. (1963). Chimie physique. Dans la cinétique chimique. Quatrième édition, Longmans.
- L'Iran. Levine. (2009). Principes de la physicochimie. Sixième édition. Mc Graw Hill.
- Wikipédia. (2020). Équation d'Arrhenius. Récupéré de: dans.Wikipédia.org
- Guenevieve del Mundo et al. (10 septembre 2020). Équation d'Arrhenius. Récupéré de: Chem.Bibliothèque.org
- Clark Jim. (2013). Constantes de taux et l'équation d'Arrhenius. Récupéré de: Chemguide.co.ROYAUME-UNI
- Les éditeurs d'Enyclopaedia Britannica. (2020). Équation d'Arrhenius. Récupéré de: Britannica.com
- Helmestine, Anne Marie, Ph.D. (28 août 2020). La formule et l'exemple de l'équation d'Arrhenius. Récupéré de: Thoughtco.com

