Domaine et contradominium d'une fonction (avec des exemples)

Les concepts de domaine et contradiction d'une fonction Ils sont généralement enseignés dans les cours de calcul enseignés au début des carrières universitaires.

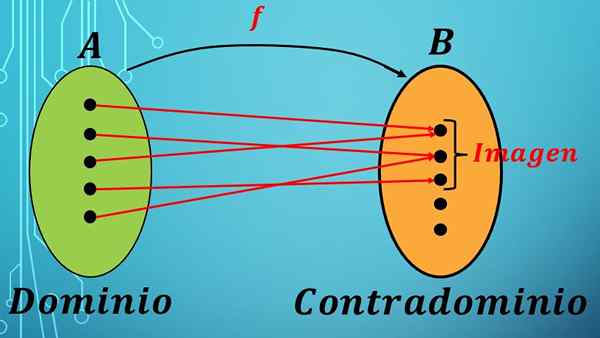
Avant de définir le domaine et la contradiction, vous devez savoir ce qu'est une fonction. Une fonction F est une loi de correspondance (règle) entre les éléments de deux ensembles.

L'ensemble dont les éléments sont choisis sont appelés le domaine de la fonction, et l'ensemble auquel ces éléments sont envoyés par F est appelé contradominium.

En mathématiques, une fonction avec le domaine A et le contradominium B est indiquée par l'expression F: A → B.

L'expression précédente indique que les éléments de l'ensemble A sont envoyés dans l'ensemble B en suivant la loi de correspondance f.

Une fonction attribue chaque élément de l'ensemble sur un seul élément de l'ensemble B.

Domaine et contradiction

Étant donné une fonction réelle d'une véritable variable f (x), le domaine de la fonction doit être tous ces nombres réels tels que, lorsqu'il est évalué en F, le résultat est un nombre réel.

Généralement, la contradiction d'une fonction est l'ensemble des nombres N réels. La contradiction est également appelée l'ensemble d'arrivée ou de codominium de la fonction F.

La contradiction d'une fonction est toujours r?

Non. Tant que la fonction n'est pas étudiée en détail, l'ensemble des nombres N réels est généralement considéré comme une contradiction.

Mais une fois la fonction étudiée, un ensemble plus approprié peut être considéré comme contradominium, qui sera un sous-ensemble de R.

L'ensemble approprié mentionné dans le paragraphe précédent coïncide avec l'image de la fonction.

La définition de l'image ou de la plage d'une fonction F fait référence à toutes les valeurs qui proviennent de l'évaluation d'un élément du domaine en f.

Exemples de domaine et de contradiction

Dans les exemples suivants, comment calculer le domaine d'une fonction et son image est illustrée.

Exemple 1

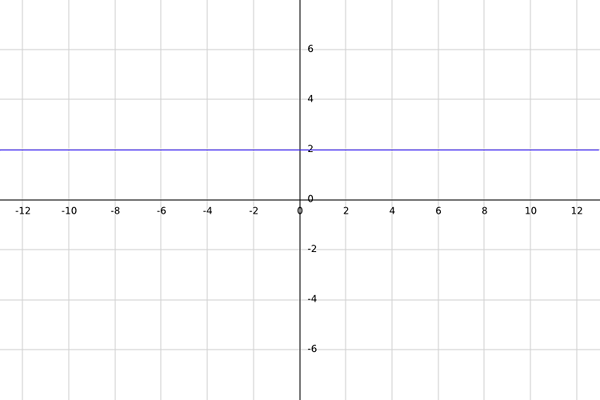
Soit f une fonction réelle définie par f (x) = 2.

Le m-domaine de f est tous les nombres réels tels que, lors de leur évaluation en F, le résultat est un nombre réel. La contradiction pour le moment est égale à r.

Comme la fonction donnée est constante (toujours égale à 2), il doit à ce que le nombre réel soit choisi, car lorsque l'évaluation en F, le résultat sera toujours égal à 2, ce qui est un nombre réel.

Par conséquent, le domaine de la fonction donnée est tous les nombres réels; c'est-à-dire a = r.

Maintenant qu'il est déjà connu que le résultat de la fonction est toujours égal à 2, l'image de la fonction n'est que le nombre 2, donc la contradiction de la fonction peut être redéfinie comme b = img (f) = 2.

Par conséquent, f: r → 2.

Exemple 2

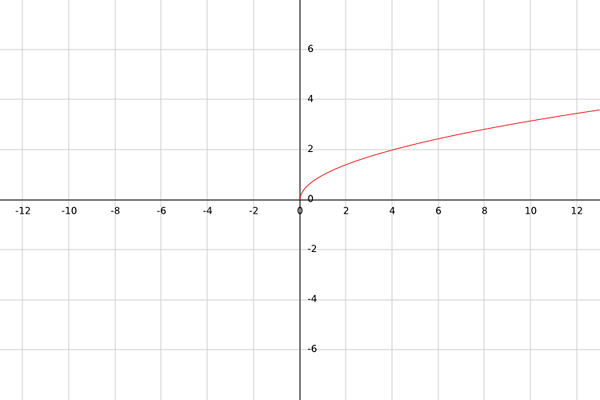
Soit g une fonction réelle définie par g (x) = √x.

Tant que l'image de g n'est pas connue, la contradominium de g est b = r.

Avec cette fonction, il convient de prendre en compte que les racines carrées ne sont définies que pour les nombres non négatifs; c'est-à-dire pour les nombres supérieurs ou égaux à zéro. Par exemple, √-1 n'est pas un nombre réel.

Par conséquent, la maîtrise de la fonction G doit être tous les nombres supérieurs ou égaux à zéro; c'est-à-dire x ≥ 0.

Par conséquent, a = [0, + ∞).

Pour calculer la plage, il convient de noter que tout résultat de g (x), car il s'agit d'une racine carrée, sera toujours supérieure ou égale à. C'est-à-dire b = [0, + ∞).

En conclusion, g: [0, + ∞) → [0, + ∞).

Exemple 3

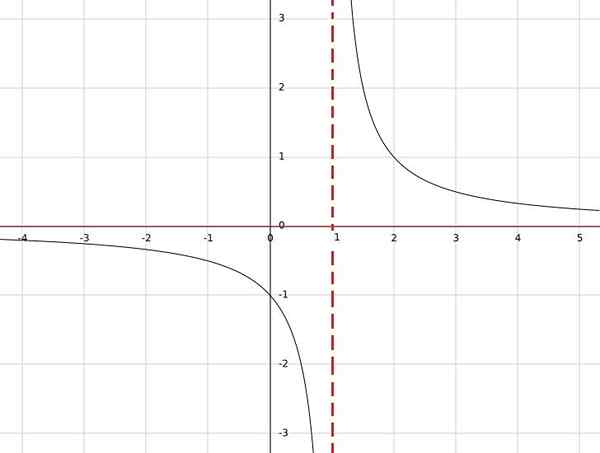
Si vous avez la fonction h (x) = 1 / (x-1), cette fonction n'est pas définie pour x = 1, car dans le dénominateur, il serait obtenu zéro et la division par zéro n'est pas définie.

D'un autre côté, pour toute autre valeur réelle, le résultat sera un nombre réel. Par conséquent, le domaine est tous reais sauf un; c'est-à-dire a = r \ 1.

De la même manière, on peut voir que la seule valeur qui ne peut pas être obtenue en conséquence est 0, car pour qu'une fraction soit égale à zéro, le numérateur doit être nul.

Par conséquent, l'image de la fonction est l'ensemble de tous les reais sauf zéro, alors il est considéré comme contradominium b = r 0.

En conclusion, H: R \ 1 → R \ 0.

Observations

Le domaine et l'image ne doivent pas être le même ensemble, comme démontré dans les exemples 1 et 3.

Lorsqu'une fonction est graphique au plan cartésien, le domaine est représenté par l'axe x et la contradominium ou la plage est représentée par l'axe y.